题目一

试题编号： 201312-3
试题名称： 最大的矩形
时间限制： 1.0s
内存限制： 256.0MB
问题描述：
问题描述
　　在横轴上放了n个相邻的矩形，每个矩形的宽度是1，而第i（1 ≤ i ≤ n）个矩形的高度是hi。这n个矩形构成了一个直方图。例如，下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。

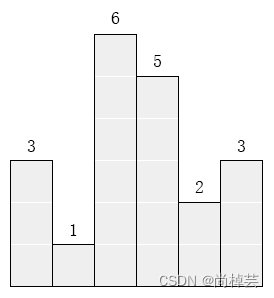
请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是10。

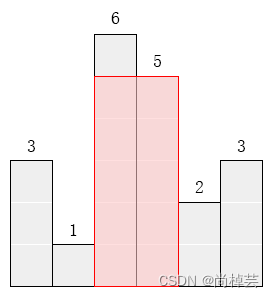
输入格式
　　第一行包含一个整数n，即矩形的数量(1 ≤ n ≤ 1000)。
　　第二行包含n 个整数h1, h2, … , hn，相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
输出格式
　　输出一行，包含一个整数，即给定直方图内的最大矩形的面积。
样例输入
6
3 1 6 5 2 3
样例输出
10

题目分析（个人理解）

1. 此题输入第一行n表示有几个矩阵，第二行表示每个矩阵有多高。输出一行，包含一个整数，即给定直方图内的最大矩形的面积。
2. 我的理解如下，可以先将所有的矩阵的高都存入列表（宽都是1），用total作为统计当前矩形面积的最大值，只需先遍历每一个矩阵，判断当前矩阵的高存入h,当前最大面积存入area。如果下一个遍历的矩阵的高比当前h小则替换h，然后求面积，更新area(最大面积)。最后输出total即可。
3. 上代码！！！

n=int(input())
nums=list(map(int,input().split()))
total=0
for i in range(n):
    h=nums[i]
    area=nums[i]
    for j in range(i+1,n):
        if h>nums[j]:
            h=nums[j]
        area=max(area,h*(j-i+1))
    total=max(total,area)
print(total)

题目二

试题编号： 201312-4
试题名称： 有趣的数
时间限制： 1.0s
内存限制： 256.0MB
问题描述：
问题描述
　　我们把一个数称为有趣的，当且仅当：
　　1. 它的数字只包含0, 1, 2, 3，且这四个数字都出现过至少一次。
　　2. 所有的0都出现在所有的1之前，而所有的2都出现在所有的3之前。
　　3. 最高位数字不为0。
　　因此，符合我们定义的最小的有趣的数是2013。除此以外，4位的有趣的数还有两个：2031和2301。
　　请计算恰好有n位的有趣的数的个数。由于答案可能非常大，只需要输出答案除以1000000007的余数。
输入格式
　　输入只有一行，包括恰好一个正整数n (4 ≤ n ≤ 1000)。
输出格式
　　输出只有一行，包括恰好n 位的整数中有趣的数的个数除以1000000007的余数。
样例输入
4
样例输出
3

题目分析（个人理解）

1. 题目很简洁，还是先看输入，要求输入n<=1000,这是一道排列组合题，需要找到数学规律是关键。
2. 总共n位数，设其中0和1的个数有k位，2和3的位数就是n-k位，又因为0 1 2 3至少出现一次，那么
3. 第一位只可能是2
4. 代码如下：

n = int(input())
MOD = 10**9 + 7
c = [[0 for i in range(1001)] for j in range(1001)]  # n<=1000
for i in range(0, 1001):
    c[i][0] = 1
    for j in range(1, i+1):
        c[i][j] = (c[i-1][j-1] + c[i-1][j]) % MOD

num = 0
for k in range(2, n-1):  # 连加
    num += c[n-1][k]*(k-1)*(n-k-1)  # c[][]为组合数
print(num % MOD)

总结

三四题真的难。