本题思路来源于acwing算法提高课
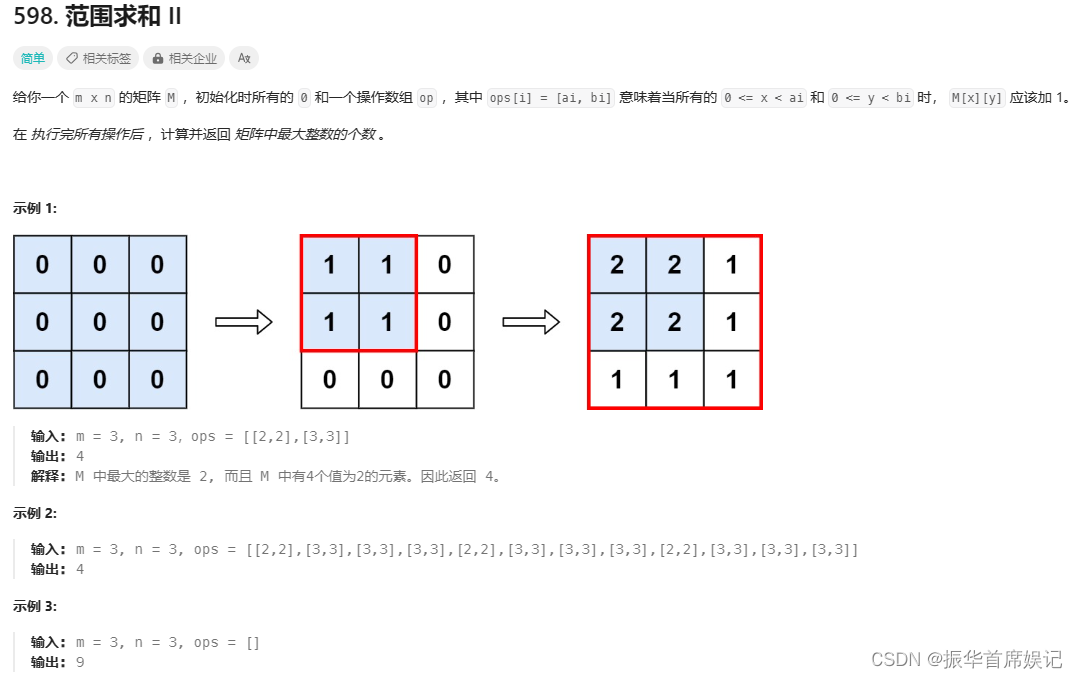
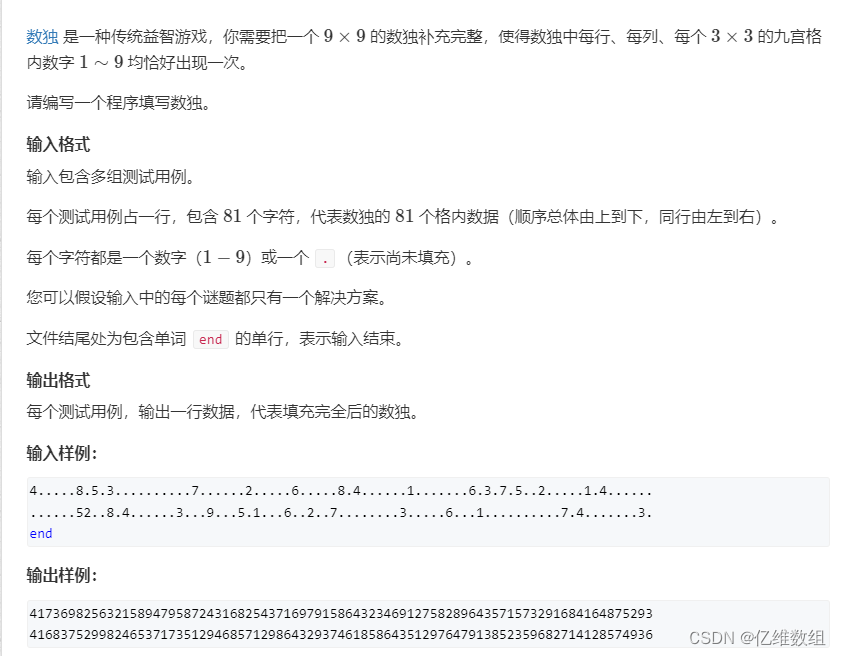
题目描述
看本文需要准备的知识
1.dfs算法基本思想
2.位运算基础
3.对剪枝这个名词的大概了解
剪枝优化+位运算优化
常见四种剪枝策略

首先考虑这道题的搜索顺序,很明显,可以随意选择一个空格子,分支为这个空格子可以填入的所有数字,然后对于每个分支,可以再随意选择一个空格子,继续进行上述步骤达成递归,这种搜索顺序是一定能够把每一种情况不漏地搜索到
下面考虑优化的策略:
第一个优化,优化搜索顺序,可以考虑一下,什么情况下,搜索的分支较少呢?显然是对于那些可以填的数字合法情况比较少的空格,所以我们再找下一个空格时,就优先选择这类的空格
上面的搜索顺序保证了不会有冗余,所以第二个剪枝策略用不上
第二个优化,可行性剪枝,就是说在遍历过程当中,只考虑那些合法的数字分支,即在那个空格的行、列以及九宫格上面不能有数字重复
最优性剪枝也是用不上的,因为这里面只要找到一个合法解就行了,不存在最优解的区分
第三个优化是位运算,用来做两件事情:
1.用一个9位的01串表示一行或一列或一个九宫格里面的填充情况,0表示已经填充,1表示没有填充,举一个例子,row[2]=000111010表示第二行已经用过了9,8,7,3,1,列col和九宫格cell同理,那么对于一个坐标为(x,y)的空格,怎么知道可以填哪些数字呢?只需要把对应的row、col、cell进行与运算,看一下1出现了第几位上,那么就可以填几
2.lowbit优化
lowbit是什么?是一个运算,比如lowbit(x)=x&-x
lowbit可以算出什么?比如10101可以得到1,100100可以得到100,11000可以得到1000(注意上面的都是二进制数,即得到最低位1的位置)
有了lowbit之后,对于一个空格,假设我们通过上面二进制表示的行、列、九宫格的与运算得到了一个01串:101001010,这个01串有4个1,如果直接遍历,每次都要9次,但是如果用上lowbit,只需要遍历4次即可:
lowbit(101001010)=10,第2位的1,所以可以放2
lowbit(101001000)=1000,第4位的1,所以可以放4
依次类推......
详细过程
讲解了本题的优化策略,下面来详细介绍,这道题的实现细节
首先定义6个数组:
其中三个为int row[N],col[N],cell[N][N],存放对应位置的状态
第四个是int ones[1<<N],表示某一个数的二进制表示里面有几个1
第五个是int log2[1<<N],表示某一个数的以2为底的对数,因为使用lowbit之后得到的是2的k次幂,而这个k才是我们想要的(代表1的位置),所以我们预处理这个数组,方便后续使用
第六个就是char str[100],代表所有的格子内容,包括数字和小数点(表示暂时没有填充)这两种情况
然后再写四个辅助函数,分别是init,draw,get_state,lowbit
init:初始化所有格子,暂时全部没有填过数字
draw:在(x,y)这个格子上面填上数字t(is_set==true),或者去掉数字t(is_set==false)
get_state:得到(x,y)上的行、列、九宫格的状态交集01串
lowbit:上面已经讲解过了
然后我们来说一下main函数的内容:
对于每一个样例,init初始化,然后遍历输入的str,对方格进行填充,如果遇到’.’那么就记录一下,最终统计暂未填充的格子总数,最后调用dfs,最后输出str即可
最后我们说dfs如何写:
首先参数cnt代表还剩几个空格没有填数,当cnt==0时,直接返回true即可,表示已经全部填充完毕。
然后,寻找分支数最少的空格(搜索顺序优化)
找到之后,通过get_state函数得到01串,然后利用lowbit去得到这个01串中1的每个位置,就是一个新的分支,这个遍历之后返回false保证函数代码的完整性
完整代码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=9,M=1<<N;
int row[N],col[N],cell[N][N];
int ones[M],log2_map[M];
char str[100];
void init()
{
for(int i=0;i<N;i++)row[i]=col[i]=(1<<N)-1;
for(int i=0;i<N/3;i++)
{
for(int j=0;j<N/3;j++)cell[i][j]=(1<<N)-1;
}
}
void draw(int x,int y,int t,bool is_set)
{
if(is_set)str[x*N+y]=t+'1';
else str[x*N+y]='.';
int r=1<<t;
if(!is_set)r=-r;
row[x]-=r;
col[y]-=r;
cell[x/3][y/3]-=r;
}
int lowbit(int x)
{
return x&-x;
}
int get_state(int x,int y)
{
return row[x]&col[y]&cell[x/3][y/3];
}
bool dfs(int cnt)
{
if(!cnt)return true;
int minx=10;
int x,y;
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
if(str[i*N+j]=='.')
{
int state=get_state(i,j);
if(ones[state]<minx)
{
minx=ones[state];
x=i,y=j;
}
}
}
}
int state=get_state(x,y);
for(int i=state;i;i-=lowbit(i))
{
int t=log2_map[lowbit(i)];
draw(x,y,t,true);
if(dfs(cnt-1))return true;
draw(x,y,t,false);
}
return false;
}
int main()
{
for(int i=0;i<N;i++)log2_map[1<<i]=i;
for(int i=0;i<1<<N;i++)
for(int j=0;j<N;j++)
ones[i]+=(i>>j)&1;
while(cin>>str,str[0]!='e')
{
init();
int cnt=0;
for(int i=0,k=0;i<N;i++)
{
for(int j=0;j<N;j++,k++)
{
if(str[k]!='.')
{
draw(i,j,str[k]-'1',true);
}
else
cnt++;
}
}
dfs(cnt);
cout<<str<<endl;
}
return 0;
}