---

前言

---

提示：我宁愿做自己，做卑微的自己，也不愿做别人，无论那会多么快乐。 --《美丽新世界》

我们在数组和链表的部分就已经接触到了双指针的思想，这里我们继续扩展了解滑动窗口的思想。滑动窗口其实也是双指针的一种特殊场景，这种方式可以很好的解决一些特定场景的问题，就有了”滑动窗口思想“

滑动窗口的基本思想

在数组和链表的章节，都强调过移动元素的方法。有一些经典的例子，推荐回顾再看一下⭐⭐⭐：

算法通过村第三关-数组白银笔记|数组双指针_师晓峰的博客-CSDN博客

算法通关村第一关-链表白银挑战笔记|公共子节点_师晓峰的博客-CSDN博客

于是慢慢的方式更加完善，这就有了”双指针的思想“

在数组双指针里，我们介绍过”对撞型”、“快慢型“两种方式，而滑动窗口思想其实也就是快慢型的特例。我们在学习计算机网络的同学都直到欢动窗口协议（Sliding Window Protocol)，该协议是TCP实现流量控制等核心策略之一。事实上与流量控制，熔断、限流、超时等场景下都会首先从滑动窗口的角度来思考问题，比如Hystrix，sentinel等框架都使用了这种思想。

滑动窗口的思想非常简单，如下图，假如窗口的大小是3，当不断有新数据来的时候，我们便维护一个大小为3的一个区间，超过3的就将新的加入，老的移走。

这个过程有点像火车在轨道上行驶，原始数据可能在一个很大的空间里（铁轨），但是我们标记的小区间就像是一列固定长度的过车，一直再向前走。

有了区间，造其题目来就很容易了，例如让你找序列上连续数字的最大和最小，或者平均数，等等问题把

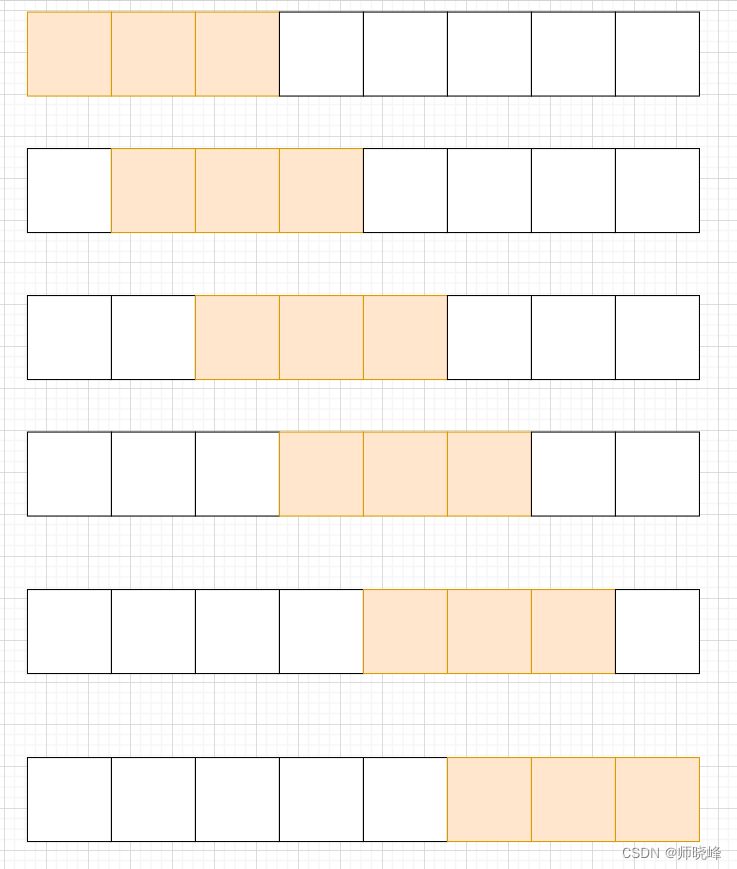
从上面看，刚才的形容是不是非常形象，所谓的窗口就是建立两个索引，left和right，并保持{left，right}之间的长度不变，然后一遍遍历，一遍寻找目标，每次更改目标要求就可以。

当然上面的例子已经告诉我们什么是窗口，什么是滑动的窗口：

• 窗口：窗口其实就是两个变量left和right之间的元素，也可以理解为一个区间。窗口的大小可能是固定的，也可能是变换的，如果是固定大小的，那么自然要考虑是否越界，在执行处理逻辑。如果不是固定的，就要优先判断是否满足要求，再执行逻辑处理。
• 滑动：说明这个窗口是移动的，事实上移动的仍然是left和right两个变量，而不是序列中的元素。当变量移动的时候，其中间的元素必然也会发生变化，因此就有了不断滑动的效果。

在实际问题中，窗口大小不一定是固定的，我们可以思考以下两种场景：

1. 固定窗口的滑动就是火车行驶这种大小不变的移动
2. 可变的窗口就是两个老师带着一队学生外出，一个负责开路，一个负责断后，中间则是小朋友。两个老师直接的距离有可能大有可能小，但是整体窗口是不断滑动向前的

所以根据窗口大小是否固定，就衍生出两种类型的题目：

1. 固定窗口：一般让你求那个窗口的元素最大，最小、平均值、和最大、和最小等等类型的问题。
2. 窗口变化：则一般是让你求序列最大、最小窗口是什么等等。

滑动窗口题目本身没有很大难度，但是在实际的解答中还是比较难搞的，主要是以下原因：

1. 容器：数组，让人头疼的边界问题，稍不注意，就全盘皆输。
2. 元素处理：比较、判断等处理方式上不仅需要借助集合等工具，还要处理技巧，不熟悉的话拿不下来。
3. 堆：堆的接口很适合做数据处理。在固定的区间找最大、最小等问题上有很大优势。一次常常滑动窗口会和堆一起使用完美的解决很多复杂问题。

最后的疑惑：双指针和滑动窗口有什么区别？

根据性质可以看出，滑动窗口就是双指针应用的特例，主要是关注两个指针间的元素情况，因此范围更小，双指针的应用范围更广，花样更多。

入门题目练习

滑动窗口的题目在于窗口的大小变或者不变,根据这两种类型,我们就先来练练手吧.

子数组最大平均数

参考题目介绍:643. 子数组最大平均数 I - 力扣（LeetCode）

这是经典的滑动窗口的例子,况且大小都规定了,我们只要先读取k个,然后让窗口向前移动就可以了,思路和上图一模一样．

直接展示代码:

    /**
     * 子数组最大平均数 I
     * @param nums
     * @param k
     * @return
     */
    public static double findMaxAverage(int[] nums, int k) {
        int len = nums.length;
        if ((k > len) || (len < 1) || (k < 1)) {
            return 0;
        }
        // 第一步确定窗口大小
        int windowSum = 0;
        for (int left = 0; left < k; left++) {
            windowSum += nums[left];
        }
        // 第二步 遍历维护窗口  保留窗口,处理元素
        int res = windowSum;
        for(int right = k; right < len; right++){
            windowSum += (nums[right] - nums[right - k]);
            res = Math.max(res,windowSum);
        }
        return (double) res / k;
    }

最长连续递增序列

参考题目介绍:674. 最长连续递增序列 - 力扣（LeetCode）

根据实例我们看图:

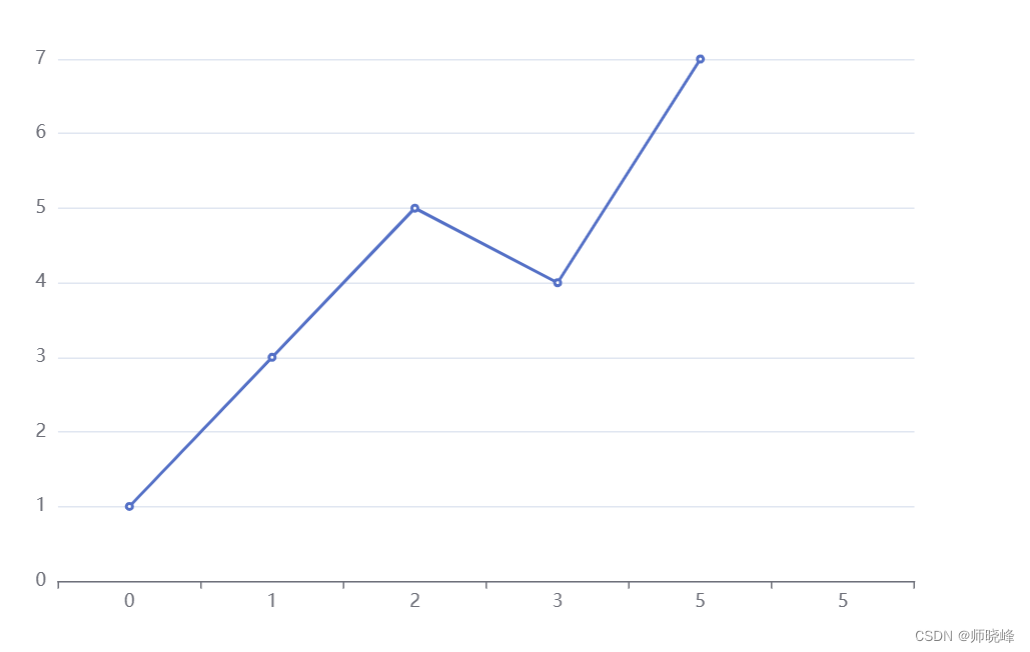
可以看到,最长的递增子序列为{1,3,5},所以返回3.在遍历的时候从第第一个元素开,先定义窗口区间[left,right),

表示递增序列,具体操作如下:

1. 如果当前遍历到的元素比左边的那个元素要严格大,right就增加;
2. 相反,left就跳到right的其实位置,重新计算.

这里看下代码怎么写:

/**
 * 674. 最长连续递增序列
 * @param nums
 * @return
 */
public static int findLengthOfLCIS_1(int[] nums) {
   int len = nums.length;;
   int left = 0,right = 0;
   int res = 0;
   while(right < len){
       // 严格递增 right++
       // 相反 right 赋值给left (本质也是快慢指针问题
       if (right >0 && nums[right - 1] >= nums[right]){
           left = right;
       }
       right++;
       res = Math.max(res,right - left);
   }
   return res;
}

上面的代码中,序列在[left,right)下严格递增,区间的长度是right-left.

这里还有很多解法,另外一种简单的思路是一遍遍历,一边统计每个递增区间的长度.如果长度超过之前所有的区间,就保留,代码写起来也很容易:

    /**
     * 674. 最长连续递增序列
     *
     * @param nums
     * @return
     */
    public static int findLengthOfLCIS_2(int[] nums) {
        int currentSum = 1;
        int res = 1;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i - 1] >= nums[i]) {
                // 说明不满足条件，重新计数
                currentSum = 1;
            }else{
                currentSum++;
            }
            res = Math.max(res, currentSum);
        }
        return res;
    }

当然本题目你如果不知道滑动窗口,也可以做的,不要觉得它过于神秘,只是个名字而已,掌握方法,看透本质才是主要的.

---

总结

提示：滑动窗口；双指针；快慢指针变体；滑动窗库概念；滑动窗口核心理解

---

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ ("▔□▔)/

如有不理解的地方，欢迎你在评论区给我留言，我都会逐一回复 ~

也欢迎你 关注我 ，喜欢交朋友，喜欢一起探讨问题。