分发糖果[困难]

news2024/12/23 22:34:40

优质博文：IT-BLOG-CN

一、题目

n个孩子站成一排。给你一个整数数组ratings表示每个孩子的评分。你需要按照以下要求，给这些孩子分发糖果：
【1】每个孩子至少分配到1个糖果。
【2】相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果，计算并返回需要准备的最少糖果数目。

示例 1：
输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发2、1、2颗糖果。

示例 2：
输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发1、2、1颗糖果。第三个孩子只得到1颗糖果，这满足题面中的两个条件。

n == ratings.length
1 <= n <= 2 * 104
0 <= ratings[i] <= 2 * 104

二、代码

【1】两次遍历： 我们可以将「相邻的孩子中，评分高的孩子必须获得更多的糖果」这句话拆分为两个规则，分别处理。
左规则： 当ratings[i−1] < ratings[i]时，i号学生的糖果数量将比i−1号孩子的糖果数量多。
右规则： 当ratings[i] > ratings[i+1]时，i号学生的糖果数量将比i+1号孩子的糖果数量多。
我们遍历该数组两次，处理出每一个学生分别满足左规则或右规则时，最少需要被分得的糖果数量。每个人最终分得的糖果数量即为这两个数量的最大值。

具体地，以左规则为例：我们从左到右遍历该数组，假设当前遍历到位置i，如果有ratings[i−1] < ratings[i]那么i号学生的糖果数量将比i−1号孩子的糖果数量多，我们令left[i]=left[i−1] + 1即可，否则我们令left[i] = 1。在实际代码中，我们先计算出左规则left数组，在计算右规则的时候只需要用单个变量记录当前位置的右规则，同时计算答案即可。

class Solution {
    public int candy(int[] ratings) {
        // 1、定义left[]数组，计算每个小朋友符合左侧规则时，能获取到的糖果
        // 2、定义两个变量，第一个计算前一个小朋友的糖果，第二个计算总的糖果数量，从右侧开始计算
        if (ratings.length == 0) {
            return 0;
        }
        // 创建数组
        int[] left = new int[ratings.length];
        left[0] = 1;
        for(int i = 1; i < ratings.length; i++) {
            if (ratings[i] > ratings[i - 1]) {
                left[i] = left[i - 1] + 1;
            } else {
                left[i] = 1;
            }
        }
        // 先初始化最后一个小朋友的糖果
        int next = 1, count = Math.max(1, left[ratings.length - 1]);
        for(int i = ratings.length - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {
                next += 1;
            } else {
                next = 1;
            }
            count += Math.max(next, left[i]);
        }
        return count;
    }
}

时间复杂度： O(2n)其中n是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。
空间复杂度： O(n)其中n是孩子的数量。我们需要保存所有的左规则对应的糖果数量。

【2】常数空间遍历： 定义两个变量，第一个计算当前小朋友的糖果pre，第一个小朋友默认为1，第二个计算总的糖果数量count，如果时递增的，那么就比较简单，我们给pre+1，如果递减了，我们重置pre = 1即可。下面考虑两个特殊场景：
● 当pre=1时，开始递减时，我们需要再创建一个变量decr，来表示递减的次数，然后将其累积到count中，也就达到了将递减转化为递增的效果。
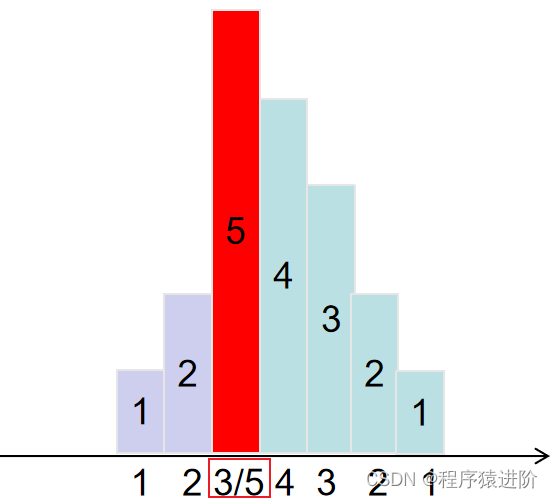
● 当递减的队列长度，超过了递减前小朋友的糖果时，我们需要对递减前的小朋友的糖果+n，例如下图: 从左侧遍历时，第三个小朋友应该是3个糖果，所以定义inc记录递减前小朋友的糖果，如果递减的糖果decr等于递减前的糖果inc,就需要对inc + 1；

class Solution {
    public int candy(int[] ratings) {
        // 1、定义两个变量，第一个计算当前小朋友的糖果pre，第二个计算总的糖果数量count。
        // 2、左侧遍历时，如果时递减的情况，需要再创建一个变量，计算递减的次数 decr。
        // 3、特殊处理：递减的时候，如果我拥有的糖果和递减前小朋友的糖果个数相同时，需要++，举例：5321的时候，5有3个糖果，此时的3再递减中也会有5个糖果，所以就需要对5的糖果+1
        if (ratings.length == 0) {
            return 0;
        }
       
        // 先初始化最后一个小朋友的糖果
        int pre = 1, count = 1, decr = 0, inc = 1;
        for(int i = 1; i < ratings.length; i++) {
            if (ratings[i] >= ratings[i - 1]) {
                pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;;
                // 如果时递增的，当前递减序列结束
                decr = 0;
                count += pre;

                // pre表示当前小朋友用于的当过
                inc = pre;
            } else {
                // 如果开始了递减序列，我们就开始记录递减序列的长度
                decr++;
                // 递减的时候，如果我拥有的糖果和递减的小朋友的个数相同时，需要++，举例：5321的时候，5有3个糖果，此时的3再递减中也会有5个糖果，所以就需要对5+1
                if (inc == decr) {
                    decr++;
                }
                // 重置糖果为1
                pre = 1;
                count += decr;
            }
        }
        return count;
    }
}