[NOIP2000 提高组] 方格取数 - 洛谷

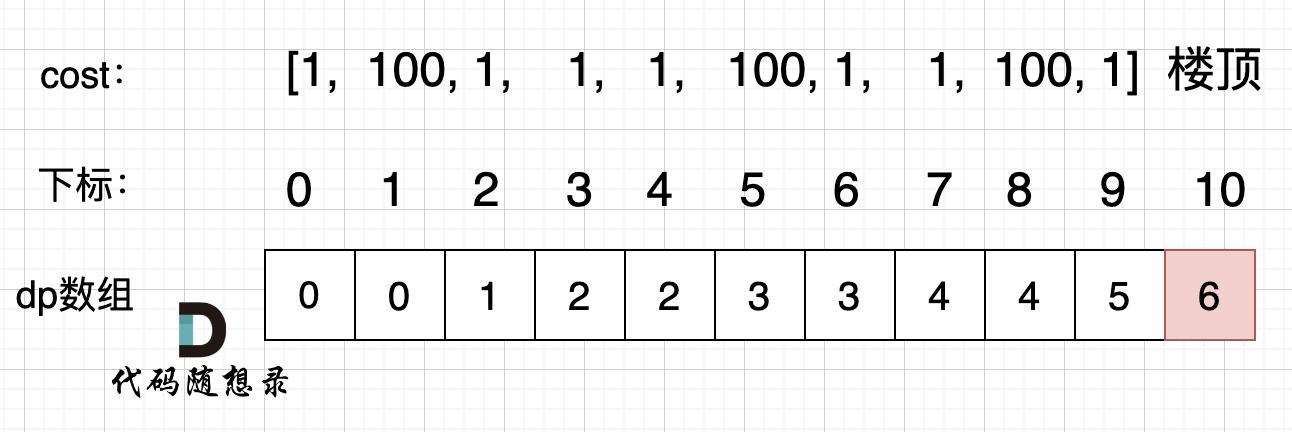
用四维dp数组存储，如果两个路线走到重复点，减去一个当前位置的值即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 11;
int grid[N][N] = {0};
int dp[N][N][N][N] = {0};
int n, i, j, tmp;
void solve(int n){
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){
			for(int k = 1; k <= n; k++){
				for(int m = 1; m <= n; m++){
					
					int tmp1 = max(dp[i - 1][j][k][m - 1], dp[i][j - 1][k - 1][m]);
					int tmp2 = max(dp[i - 1][j][k - 1][m], dp[i][j - 1][k][m - 1]);
					int now = grid[i][j] + grid[k][m];
					if(i == k && j == m) now -= grid[i][j];
					dp[i][j][k][m] = max(dp[i][j][k][m], max(tmp1, tmp2) + now);
				}
			}
		}
	} 
}
int main(){
	cin >> n;
    while(cin>>i>>j>>tmp){
    	if(!i && !j && !tmp) break;
    	grid[i][j] = tmp;
	}
	solve(n);
	cout<<dp[n][n][n][n]<<endl;
	return 0;
}