与GAN的那篇笔记相同, 做一下笔记. 并不是全文翻译, 只翻译一部分.
原文地址: from AutoEncoder to Beta-VAE
0. 前言
自编码器是用来重构高维数据的,它利用一个有bottleneck层的神经网络。bottleneck层获取压缩的潜在编码,这样将嵌入向量以低维表示可以应用在许多地方,例如搜索,数据压缩,或揭示数据潜在的生成因素。
本文的记号:
| 记号 | 意义 |
|---|---|
| D \mathcal{D} D | 数据集 大小为n |
| x ( i ) x^{(i)} x(i) | 数据集中的样本,维数为d |
| x x x | 数据集中的样本 |
| x ′ x' x′ | x x x的重建版本 |
| x ~ \tilde{x} x~ | x x x经噪声腐蚀的版本 |
| z z z | bottleneck学习到的压缩编码 |
| a j ( l ) a_j^{(l)} aj(l) | 第l层第j个神经元的激活函数 |
| g ϕ ( ) g_\phi() gϕ() | 编码器函数, 参数为 ϕ \phi ϕ |
| f θ ( ) f_\theta() fθ() | 解码器函数, 参数为 θ \theta θ |
| q ϕ ( z / x ) q_\phi(z/x) qϕ(z/x) | 估计的后验概率函数, 也就是概率编码器 |
| p θ ( x / z ) p_\theta(x/z) pθ(x/z) | 给定编码 z z z能生成真实样本概率, 也就是概率解码器 |
1. 自编码器
自编码器就是被设计用来以一个无监督方式学习一个恒等映射的神经网络, 它在重建输入的过程中发现一个更加高效和压缩的数据表示. 由两部分组成:
- 编码器网络: 将高维的输入变成潜在的低维编码.
- 解码器网络: 解码器从编码重建输入.
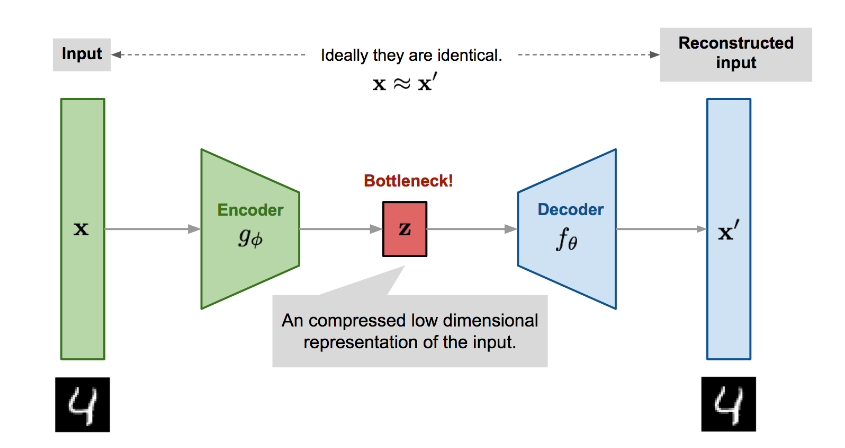
编码器的表达式为 z = g ϕ ( x ) z=g_\phi(x) z=gϕ(x), 解码器重建输入的表达式为 x ′ = f θ ( g ϕ ( x ) ) x'=f_\theta(g_\phi(x)) x′=fθ(gϕ(x)).
参数
θ
,
ϕ
\theta, \phi
θ,ϕ是一起训练的, 我们让输出与输入尽可能接近, 于是规定以下的损失函数(均方误差损失):
L
AE
(
θ
,
ϕ
)
=
1
n
∑
i
=
1
n
(
x
(
i
)
−
f
θ
(
g
ϕ
(
x
(
i
)
)
)
)
2
L_\text{AE}(\theta, \phi) = \frac{1}{n}\sum_{i=1}^n (\mathbf{x}^{(i)} - f_\theta(g_\phi(\mathbf{x}^{(i)})))^2
LAE(θ,ϕ)=n1i=1∑n(x(i)−fθ(gϕ(x(i))))2
2. 去噪自编码器
然而, 上述的自编码器容易面临过拟合的风险, 于是有人提出了去噪自编码器, 也就是输入是部分地被加性噪声或者是遮挡的mask给侵蚀了, 也就是 x ~ ∼ M D ( x ~ ∣ x ) \tilde{\mathbf{x}} \sim \mathcal{M}_\mathcal{D}(\tilde{\mathbf{x}} \vert \mathbf{x}) x~∼MD(x~∣x), M D \mathcal{M}_\mathcal{D} MD就是原本的数据样本到被侵蚀的样本的映射. 这样模型在训练的时候仍旧被要求恢复完整的输入:
x ~ ( i ) ∼ M D ( x ~ ( i ) ∣ x ( i ) ) L DAE ( θ , ϕ ) = 1 n ∑ i = 1 n ( x ( i ) − f θ ( g ϕ ( x ~ ( i ) ) ) ) 2 \begin{aligned} \tilde{\mathbf{x}}^{(i)} &\sim \mathcal{M}_\mathcal{D}(\tilde{\mathbf{x}}^{(i)} \vert \mathbf{x}^{(i)})\\ L_\text{DAE}(\theta, \phi) &= \frac{1}{n} \sum_{i=1}^n (\mathbf{x}^{(i)} - f_\theta(g_\phi(\tilde{\mathbf{x}}^{(i)})))^2 \end{aligned} x~(i)LDAE(θ,ϕ)∼MD(x~(i)∣x(i))=n1i=1∑n(x(i)−fθ(gϕ(x~(i))))2
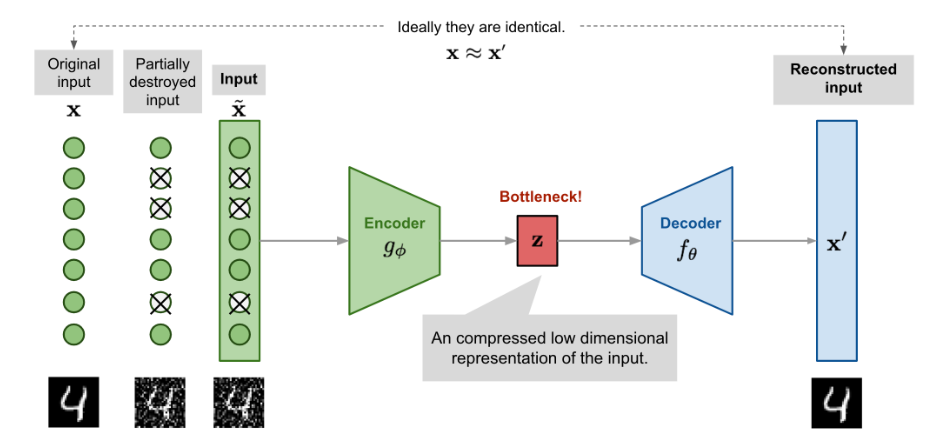
这种设计的动机是,即使视图被部分遮挡或损坏,人类也可以很容易地识别物体或场景。为了“修复”部分损坏的输入,去噪自编码器必须发现和捕获输入维度之间的关系,以便推断缺失的部分。
对于具有高冗余度的高维输入,如图像,模型可能依赖于从多个输入维度的组合中收集的证据来恢复去噪版本,而不是过度拟合一个维度。这为学习鲁棒潜在表征打下了良好的基础。
3. 稀疏自编码器
稀疏自编码器对隐藏单元激活应用“稀疏”约束,以避免过拟合和提高鲁棒性。它迫使模型同时只有少量的隐藏单元被激活,换句话说,一个隐藏神经元应该在大多数时间内处于不激活状态。
假定在第 l l l层有 s l s_l sl个神经元, 第 j j j个神经元对应的激活函数为 a j ( l ) ( . ) a^{(l)}_j(.) aj(l)(.), 被激活的神经元的比例应该是一个比较小的数, 例如0.05. 也就是说要满足如下约束:
ρ ^ j ( l ) = 1 n ∑ i = 1 n [ a j ( l ) ( x ( i ) ) ] ≈ ρ \hat{\rho}_j^{(l)} = \frac{1}{n} \sum_{i=1}^n [a_j^{(l)}(\mathbf{x}^{(i)})] \approx \rho ρ^j(l)=n1i=1∑n[aj(l)(x(i))]≈ρ
将这个约束作为一个罚项加入到损失函数中, 加入的方式是当前的激活函数比例与期望比例的KL散度. 我们将神经元被激活近似看成伯努利分布, 也就是当前被激活的神经元分布满足均值为 ρ ^ j ( l ) \hat{\rho}_j^{(l)} ρ^j(l)的伯努利分布, 期望被激活的神经元分布满足均值为 ρ \rho ρ的伯努利分布. 用KL散度衡量这两个分布的差异.
L SAE ( θ ) = L ( θ ) + β ∑ l = 1 L ∑ j = 1 s l D KL ( ρ ∥ ρ ^ j ( l ) ) = L ( θ ) + β ∑ l = 1 L ∑ j = 1 s l ρ log ρ ρ ^ j ( l ) + ( 1 − ρ ) log 1 − ρ 1 − ρ ^ j ( l ) \begin{aligned} L_\text{SAE}(\theta) &= L(\theta) + \beta \sum_{l=1}^L \sum_{j=1}^{s_l} D_\text{KL}(\rho \| \hat{\rho}_j^{(l)}) \\ &= L(\theta) + \beta \sum_{l=1}^L \sum_{j=1}^{s_l} \rho\log\frac{\rho}{\hat{\rho}_j^{(l)}} + (1-\rho)\log\frac{1-\rho}{1-\hat{\rho}_j^{(l)}} \end{aligned} LSAE(θ)=L(θ)+βl=1∑Lj=1∑slDKL(ρ∥ρ^j(l))=L(θ)+βl=1∑Lj=1∑slρlogρ^j(l)ρ+(1−ρ)log1−ρ^j(l)1−ρ
4. 变分自编码器VAE
4.1 定义
变分自编码器和上面的自编码器有很大的不同, 根植于变分贝叶斯和图模型.
自编码器是将输入映射为一个固定维数的向量, 而现在VAE将输入映射为一个分布. 假定这个分布为 p θ p_\theta pθ, 参数为 θ \theta θ, 则输入 x x x和潜在编码 z z z由以下概率完全决定:
- 先验概率 p θ ( z ) p_\theta(\mathbf{z}) pθ(z)
- 似然 p θ ( x ∣ z ) p_\theta(\mathbf{x}\vert\mathbf{z}) pθ(x∣z), 是通过潜在编码得到数据点
- 后验概率 p θ ( z ∣ x ) p_\theta(\mathbf{z}\vert\mathbf{x}) pθ(z∣x), 给定数据点推断潜在编码
现在假定我们知道真实的参数 θ ∗ \theta^{*} θ∗, 为了产生一个跟样本相似的输出, 我们这么做:
- 从分布 p θ ∗ ( z ) p_{\theta^*}(\mathbf{z}) pθ∗(z)中采样出 z ( i ) \mathbf{z}^{(i)} z(i)
- 用条件概率直接生成: p θ ∗ ( x ∣ z = z ( i ) ) p_{\theta^*}(\mathbf{x} \vert \mathbf{z} = \mathbf{z}^{(i)}) pθ∗(x∣z=z(i))
为了估计这个参数 θ ∗ \theta^{*} θ∗, 我们采用极大似然估计法, 极大似然估计的目的是让当前模型 p θ p_\theta pθ的输出在我们期望的输出(真实样本) x ( i ) \mathbf{x}^{(i)} x(i)处的概率乘积最大, 也即:
θ ∗ = arg max θ ∏ i = 1 n p θ ( x ( i ) ) \theta^{*} = \arg\max_\theta \prod_{i=1}^n p_\theta(\mathbf{x}^{(i)}) θ∗=argθmaxi=1∏npθ(x(i))
取对数:
θ ∗ = arg max θ ∑ i = 1 n log p θ ( x ( i ) ) \theta^{*} = \arg\max_\theta \sum_{i=1}^n \log p_\theta(\mathbf{x}^{(i)}) θ∗=argθmaxi=1∑nlogpθ(x(i))
现在我们将编码向量 z \mathbf{z} z加入到公式当中:
p θ ( x ( i ) ) = ∫ p θ ( x ( i ) ∣ z ) p θ ( z ) d z p_\theta(\mathbf{x}^{(i)}) = \int p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) p_\theta(\mathbf{z}) d\mathbf{z} pθ(x(i))=∫pθ(x(i)∣z)pθ(z)dz
但是计算上式需要将所有可能的 z \mathbf{z} z值采样, 这显然是不现实的, 于是我们引入一个估计函数, 这个估计函数衡量在给定输入 x \mathbf{x} x下, 编码是什么, 即 q ϕ ( z ∣ x ) q_\phi(\mathbf{z}\vert\mathbf{x}) qϕ(z∣x), 参数为 ϕ \phi ϕ.
所以 x \mathbf{x} x和 z \mathbf{z} z的关系如下图所示:
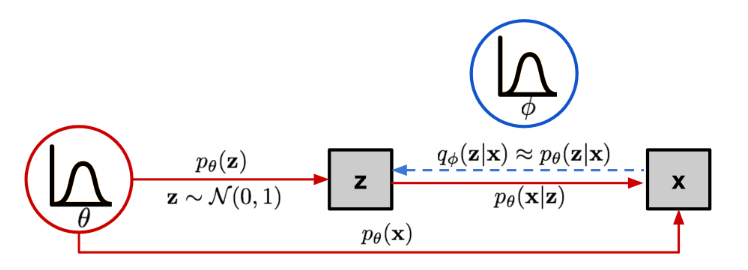
这样的结构就和自编码器有了相似之处:
- 条件概率 p θ ( x ∣ z ) p_\theta(\mathbf{x}\vert\mathbf{z}) pθ(x∣z)定义了一个生成模型, 跟自编码器中解码器角色相近. 因此也叫 概率解码器.
- 自定义估计的函数 q ϕ ( z ∣ x ) q_\phi(\mathbf{z}\vert\mathbf{x}) qϕ(z∣x)与自编码器中的编码器角色相近, 因此也叫 概率编码器.
4.2 损失函数
现在, 我们希望我们定义的 q ϕ ( z ∣ x ) q_\phi(\mathbf{z}\vert\mathbf{x}) qϕ(z∣x)与真实的分布 p θ ( x ( i ) ∣ z ) p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) pθ(x(i)∣z)尽量接近. 衡量两个分布接近的程度, 我们依旧考虑KL散度. 为此我们考虑 D KL ( q ϕ ( z ∣ x ) ∣ p θ ( z ∣ x ) ) D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) | p_\theta(\mathbf{z}\vert\mathbf{x}) ) DKL(qϕ(z∣x)∣pθ(z∣x)).
将KL散度展开:
D
KL
(
q
ϕ
(
z
∣
x
)
∥
p
θ
(
z
∣
x
)
)
=
∫
q
ϕ
(
z
∣
x
)
log
q
ϕ
(
z
∣
x
)
p
θ
(
z
∣
x
)
d
z
=
∫
q
ϕ
(
z
∣
x
)
log
q
ϕ
(
z
∣
x
)
p
θ
(
x
)
p
θ
(
z
,
x
)
d
z
; Because
p
(
z
∣
x
)
=
p
(
z
,
x
)
/
p
(
x
)
=
∫
q
ϕ
(
z
∣
x
)
(
log
p
θ
(
x
)
+
log
q
ϕ
(
z
∣
x
)
p
θ
(
z
,
x
)
)
d
z
=
log
p
θ
(
x
)
+
∫
q
ϕ
(
z
∣
x
)
log
q
ϕ
(
z
∣
x
)
p
θ
(
z
,
x
)
d
z
; Because
∫
q
(
z
∣
x
)
d
z
=
1
=
log
p
θ
(
x
)
+
∫
q
ϕ
(
z
∣
x
)
log
q
ϕ
(
z
∣
x
)
p
θ
(
x
∣
z
)
p
θ
(
z
)
d
z
; Because
p
(
z
,
x
)
=
p
(
x
∣
z
)
p
(
z
)
=
log
p
θ
(
x
)
+
E
z
∼
q
ϕ
(
z
∣
x
)
[
log
q
ϕ
(
z
∣
x
)
p
θ
(
z
)
−
log
p
θ
(
x
∣
z
)
]
=
log
p
θ
(
x
)
+
D
KL
(
q
ϕ
(
z
∣
x
)
∥
p
θ
(
z
)
)
−
E
z
∼
q
ϕ
(
z
∣
x
)
log
p
θ
(
x
∣
z
)
\begin{aligned} & D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z} \vert \mathbf{x})} d\mathbf{z} & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})p_\theta(\mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z \vert x) = p(z, x) / p(x)} \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \big( \log p_\theta(\mathbf{x}) + \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} \big) d\mathbf{z} & \\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }\int q(z \vert x) dz = 1}\\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{x}\vert\mathbf{z})p_\theta(\mathbf{z})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z, x) = p(x \vert z) p(z)} \\ &=\log p_\theta(\mathbf{x}) + \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z} \vert \mathbf{x})}[\log \frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z})} - \log p_\theta(\mathbf{x} \vert \mathbf{z})] &\\ &=\log p_\theta(\mathbf{x}) + D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) - \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) & \end{aligned}
DKL(qϕ(z∣x)∥pθ(z∣x))=∫qϕ(z∣x)logpθ(z∣x)qϕ(z∣x)dz=∫qϕ(z∣x)logpθ(z,x)qϕ(z∣x)pθ(x)dz=∫qϕ(z∣x)(logpθ(x)+logpθ(z,x)qϕ(z∣x))dz=logpθ(x)+∫qϕ(z∣x)logpθ(z,x)qϕ(z∣x)dz=logpθ(x)+∫qϕ(z∣x)logpθ(x∣z)pθ(z)qϕ(z∣x)dz=logpθ(x)+Ez∼qϕ(z∣x)[logpθ(z)qϕ(z∣x)−logpθ(x∣z)]=logpθ(x)+DKL(qϕ(z∣x)∥pθ(z))−Ez∼qϕ(z∣x)logpθ(x∣z); Because p(z∣x)=p(z,x)/p(x); Because ∫q(z∣x)dz=1; Because p(z,x)=p(x∣z)p(z)
重新整理等号两侧, 有
log p θ ( x ) − D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x ) ) = E z ∼ q ϕ ( z ∣ x ) log p θ ( x ∣ z ) − D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ) ) \log p_\theta(\mathbf{x}) - D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) = \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) logpθ(x)−DKL(qϕ(z∣x)∥pθ(z∣x))=Ez∼qϕ(z∣x)logpθ(x∣z)−DKL(qϕ(z∣x)∥pθ(z))
观察等式左边, 一方面, 我们想最大化生成数据的概率, 也就是 log p θ ( x ) \log p_\theta(\mathbf{x}) logpθ(x), 另一方面我们想最小化估计的分布与真实分布的KL散度, 也就是 D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x ) ) D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) DKL(qϕ(z∣x)∥pθ(z∣x)), 所以我们这样定义损失函数:
L VAE ( θ , ϕ ) = − log p θ ( x ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x ) ) = − E z ∼ q ϕ ( z ∣ x ) log p θ ( x ∣ z ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ) ) θ ∗ , ϕ ∗ = arg min θ , ϕ L VAE \begin{aligned} L_\text{VAE}(\theta, \phi) &= -\log p_\theta(\mathbf{x}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) )\\ &= - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}) ) \\ \theta^{*}, \phi^{*} &= \arg\min_{\theta, \phi} L_\text{VAE} \end{aligned} LVAE(θ,ϕ)θ∗,ϕ∗=−logpθ(x)+DKL(qϕ(z∣x)∥pθ(z∣x))=−Ez∼qϕ(z∣x)logpθ(x∣z)+DKL(qϕ(z∣x)∥pθ(z))=argθ,ϕminLVAE
这个损失函数被称为变分下界, 也就是 − L VAE ( θ , ϕ ) -L_\text{VAE}(\theta, \phi) −LVAE(θ,ϕ)是 log p θ ( x ) \log p_\theta (\mathbf{x}) logpθ(x)的下界(因为散度非负).
4.3 重参数化技巧
注意 z \mathbf{z} z是通过从分布 q ϕ ( z ∣ x ) q_\phi(\mathbf{z}\vert\mathbf{x}) qϕ(z∣x)中采样而来的. 但是采样是一个离散的过程, 是不可微的, 为了使网络能够训练, 我们将随机性从 z \mathbf{z} z身上转移到另一个变量身上, 也就是重参数化技巧.
我们选定另一个变量为标准高斯分布的采样, 根据高斯分布性质, 有如下关系:
z ∼ q ϕ ( z ∣ x ( i ) ) = N ( z ; μ ( i ) , σ 2 ( i ) I ) z = μ + σ ⊙ ϵ , where ϵ ∼ N ( 0 , I ) ; Reparameterization trick. \begin{aligned} \mathbf{z} &\sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) & \\ \mathbf{z} &= \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I}) & \scriptstyle{\text{; Reparameterization trick.}} \end{aligned} zz∼qϕ(z∣x(i))=N(z;μ(i),σ2(i)I)=μ+σ⊙ϵ, where ϵ∼N(0,I); Reparameterization trick.
也就是下图的关系:
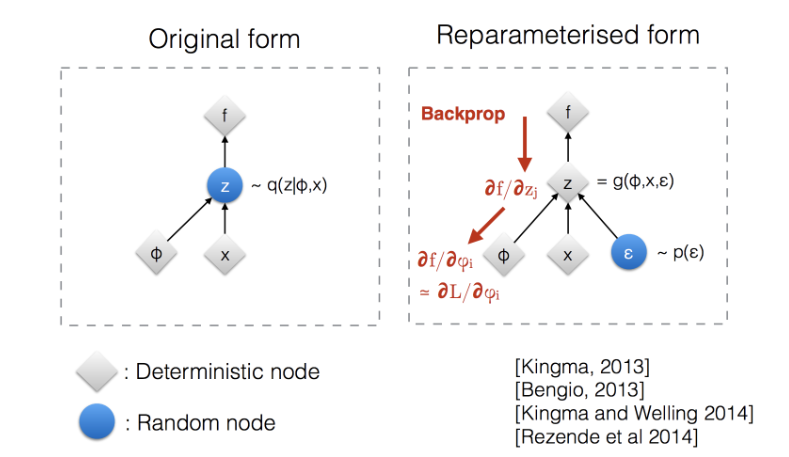
因此, 整个变分自编码器的工作流程是, 输入
x
\mathbf{x}
x, 通过估计的概率编码器
q
ϕ
(
z
∣
x
)
q_\phi(\mathbf{z}\vert\mathbf{x})
qϕ(z∣x)(
ϕ
\phi
ϕ可以是神经网络参数, 也可以是其他模型)得到均值与方差, 利用重参数化技巧得到
z
\mathbf{z}
z, 这个
z
\mathbf{z}
z就代表了输入的一个低维表示, 随后经过概率解码器
p
θ
(
x
∣
z
)
p_\theta(\mathbf{x}\vert\mathbf{z})
pθ(x∣z)(
θ
\theta
θ可以是神经网络参数, 也可以是其他模型), 得到输出
x
′
\mathbf{x}'
x′, 利用损失函数计算散度与生成概率, 进而更新参数: 如图(假定分布为多元高斯分布)







![WooCommerce Product Feed指南 – Google Shopping和Facebook[2022]](https://img-blog.csdnimg.cn/img_convert/4df72ebc8e8d5b4c78a858f2a5729304.png)







