一元高斯分布
我们从最简单最常见的一元高斯分布开始,其概率密度函数为:
p ( x ) = 1 σ 2 π e x p ( − ( x − μ ) 2 2 σ 2 ) p(x)=\frac{1}{\sigma\sqrt{2\pi}}exp(-\frac{(x-\mu)^2}{2\sigma^2}) p(x)=σ2π1exp(−2σ2(x−μ)2)
其中 μ \mu μ 和 σ \sigma σ分别表示均值和方差,这个概率密度函数曲线画出来就是我们熟悉的钟形曲线,均值和方差唯一地决定了曲线的形状。
多元高斯分布
从一元高斯分布推广到多元高斯分布,假设各维度之间相互独立
$p(x_1,x_2,\cdots,x_n)=\prod\limits_{i=1}^np(x_i)\
=\frac{1}{(2\pi)\frac{n}{2}}exp(-\frac{1}{2}[\frac{(x_1-\mu_1)2}{\sigma_12}+\frac{(x_2-\mu_2)2}{\sigma_22}+\cdots+\frac{(x_n-\mu_n)2}{\sigma_n^2}])
$
其中 μ 1 , m u 2 , ⋯ , μ 3 \mu_1,mu_2,\cdots,\mu_3 μ1,mu2,⋯,μ3和 σ 1 , σ 2 , ⋯ , σ 3 \sigma_1,\sigma_2,\cdots,\sigma_3 σ1,σ2,⋯,σ3分别是第一维,第二维到第n维的均值和方差,对上式向量和举证表示,令
x − μ = [ x 1 − μ 1 , x 2 − μ 2 , ⋯ , x n − μ n ] T x-\mu=[x_1-\mu_1,x_2-\mu_2,\cdots,x_n-\mu_n]^T x−μ=[x1−μ1,x2−μ2,⋯,xn−μn]T
K = [ σ 1 2 0 ⋯ 0 0 σ 2 2 ⋯ 0 ⋮ ⋮ ⋱ 0 0 0 0 σ n 2 ] K=\begin{bmatrix} \sigma_1^2&0&\cdots&0\\ 0&\sigma_2^2&\cdots&0\\ \vdots&\vdots&\ddots&0\\ 0&0&0&\sigma_n^2 \end{bmatrix} K= σ120⋮00σ22⋮0⋯⋯⋱0000σn2
有
σ 1 σ 2 ⋯ σ n = ∣ K ∣ 1 2 \sigma_1\sigma_2\cdots\sigma_n=\mid{K}\mid{^\frac{1}{2}} σ1σ2⋯σn=∣K∣21
( x 1 − μ 1 ) 2 σ 1 2 + ( x 2 − μ 2 ) 2 σ 2 2 + ⋯ + ( x n − μ n ) 2 σ n 2 = ( x − μ ) T K − 1 ( x − μ ) \frac{(x_1-\mu_1)^2}{\sigma_1^2}+\frac{(x_2-\mu_2)^2}{\sigma_2^2}+\cdots+\frac{(x_n-\mu_n)^2}{\sigma_n^2}= (x-\mu)^TK^{-1}(x-\mu) σ12(x1−μ1)2+σ22(x2−μ2)2+⋯+σn2(xn−μn)2=(x−μ)TK−1(x−μ)
代入得到
p ( x ) = ( 2 π ) n − 2 ∣ K ∣ 1 − 2 e x p ( 1 − 2 ( x − μ ) T K − 1 ( x − μ ) ) p(x)=(2\pi)^{\frac{n}{-2}}\mid{K}\mid^{\frac{1}{-2}}exp(\frac{1}{-2}(x-\mu)^TK^{-1}(x-\mu)) p(x)=(2π)−2n∣K∣−21exp(−21(x−μ)TK−1(x−μ))
其中 μ ∈ R n \mu\in\mathbb{R}^n μ∈Rn是均值向量, K ∈ R n × n K\in\mathbb{R^{n\times{n}}} K∈Rn×n为协方差矩阵,由于我们假设了各维度直接相互独立,因此 K K K是一个对角矩阵。在各维度变量相关时,上式的形式仍然一致,但此时协方差矩阵 不再是对角矩阵,只具备半正定和对称的性质。上式通常也简写为
x ∼ N ( μ , K ) x\sim{\mathcal{N}(\mu,K)} x∼N(μ,K)
无限元高斯分布
在多元高斯分布的基础上考虑进一步扩展,假设有无限多维呢?用一个例子来展示这个扩展的过程
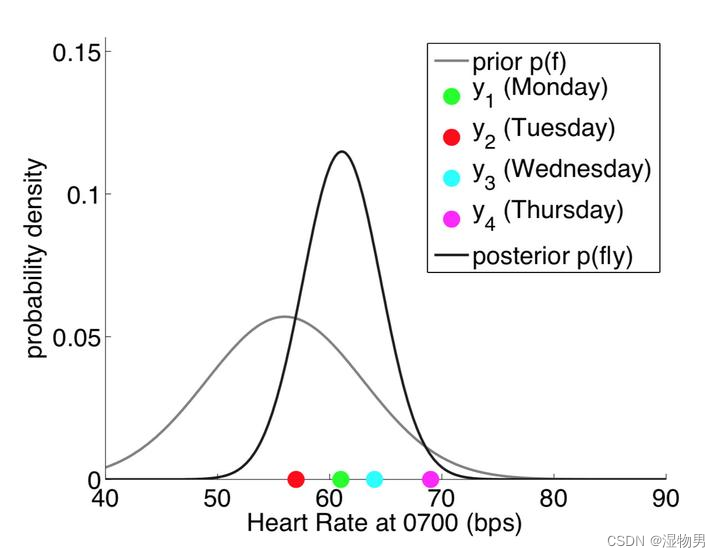
假设我们在周一到周四每天的 7:00 测试了 4 次心率,如下图中 4 个点,可能的高斯分布如图所示(高瘦的那条)。这是一个一元高斯分布,只有每天 7: 00 的心率这个维度。
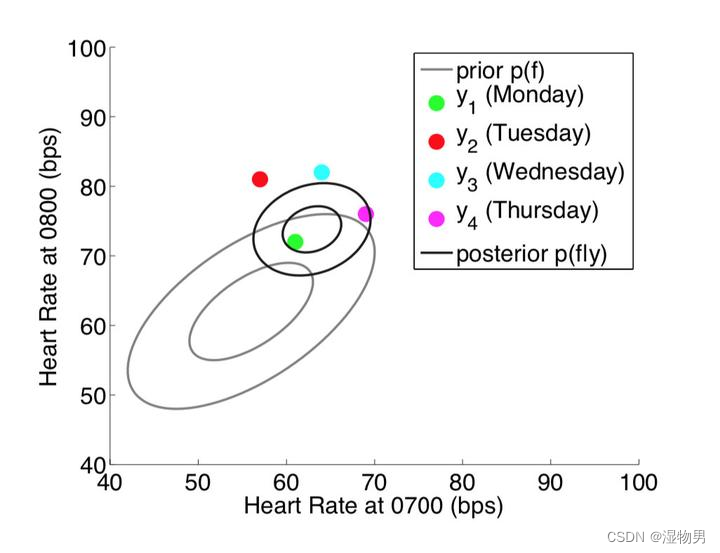
现在考虑不仅在每天的 7: 00 测心率(横轴),在 8:00 时也进行测量(纵轴),这个时候变成两个维度(二元高斯分布),如下图所示
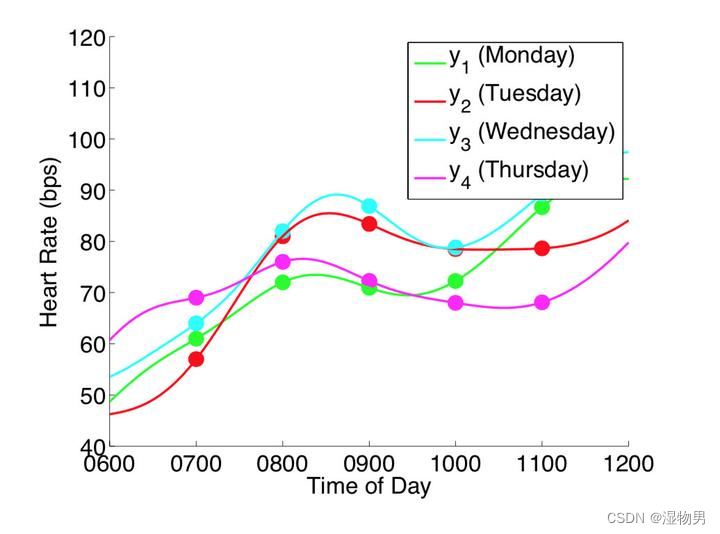
更进一步,如果我们在每天的无数个时间点都进行测量,则变成了下图的情况。注意下图中把测量时间作为横轴,则每个颜色的一条线代表一个(无限个时间点的测量)无限维的采样。当对每次对无限维进行采样得到无限多个点时,其实可以理解为我们采样得到了一个函数。
当从函数的视角去看待采样,理解了每次采样无限维相当于采样一个函数之后,原本的概率密度函数不再是点的分布 ,而变成了函数的分布。这个无限元高斯分布即称为高斯过程。高斯过程正式地定义为:对于所有 x = [ x 1 , x 2 , ⋯ , x n ] x=[x_1,x_2,\cdots,x_n] x=[x1,x2,⋯,xn] , f ( x ) = [ f ( x 1 ) , f ( x 2 ) , ⋯ , f ( x n ) ] f(x)=[f(x_1),f(x_2),\cdots,f(x_n)] f(x)=[f(x1),f(x2),⋯,f(xn)] 都服从多元高斯分布,则称 f f f是一个高斯过程,表示为
f ( x ) ∼ N ( μ ( x ) , κ ( x , x ) ) f(x)\sim\mathcal{N}(\mu(x),\kappa(x,x)) f(x)∼N(μ(x),κ(x,x))
这里 μ ( x ) : R → R n × R n \mu(x):\mathbb{R}\rightarrow \mathbb{R}^n\times{\mathbb{R}^n} μ(x):R→Rn×Rn表示均值函数(Mean function),返回各个维度的均值; κ ( x , x ) : R n × R n → R n × n \kappa(x,x):\mathbb{R}^n\times\mathbb{R}^n\rightarrow\mathbb{R}^{n\times{n}} κ(x,x):Rn×Rn→Rn×n为协方差函数 Covariance Function(也叫核函数 Kernel Function)返回两个向量各个维度之间的协方差矩阵。一个高斯过程为一个均值函数和协方差函数唯一地定义,并且一个高斯过程的有限维度的子集都服从一个多元高斯分布(为了方便理解,可以想象二元高斯分布两个维度各自都服从一个高斯分布)。
核函数(协方差函数)
核函数是一个高斯过程的核心,核函数决定了一个高斯过程的性质。核函数在高斯过程中起生成一个协方差矩阵(相关系数矩阵)来衡量任意两个点之间的“距离”。不同的核函数有不同的衡量方法,得到的高斯过程的性质也不一样。最常用的一个核函数为高斯核函数,也成为径向基函数 RBF。其基本形式如下。其中 σ \sigma σ和 l l l是高斯核的超参数。
K ( x i , x j ) = σ 2 e x p ( − ∥ x i − x j ∥ 2 2 l 2 ) K(x_i,x_j)=\sigma^2exp(-\frac{\parallel{x_i-x_j}\parallel_2^2}{l^2}) K(xi,xj)=σ2exp(−l2∥xi−xj∥22)
高斯过程可视化
下图是高斯过程的可视化,其中蓝线是高斯过程的均值,浅蓝色区域 95% 置信区间(由协方差矩阵的对角线得到),每条虚线代表一个函数采样(这里用了 100 维模拟连续无限维)。左上角第一幅图是高斯过程的先验(这里用了零均值作为先验),后面几幅图展示了当观测到新的数据点的时候,高斯过程如何更新自身的均值函数和协方差函数。
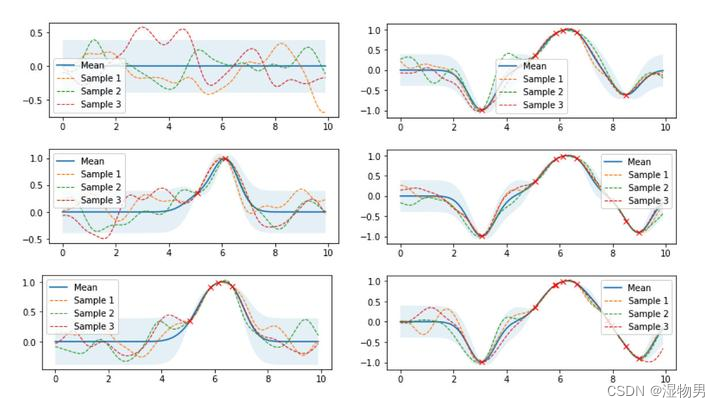
接下来我们用公式推导上图的过程。将高斯过程的先验表示为 f ( x ) ∼ N ( μ ( f ) , K f f ) f(x)\sim\mathcal{N}(\mu(f),K_{ff}) f(x)∼N(μ(f),Kff) ,对应左上角第一幅图,如果现在我们观测到一些数据 ( x ∗ , y ∗ ) (x^*,y^*) (x∗,y∗),并且假设 y ∗ y^* y∗与 f ( x ) f(x) f(x)服从联合高斯分布
[ f ( x ) y ∗ ] ∼ N ( [ μ f μ y ] , [ K f f K f y K f y T K y y ] ) \begin{bmatrix} f(x)\\ y^* \end{bmatrix} \sim\mathcal{N} \begin{pmatrix} \begin{bmatrix} \mu_f\\\mu_y \end{bmatrix} ,\begin{bmatrix} K_{ff}&K_{fy}\\K_{fy}^T&K_{yy} \end{bmatrix} \end{pmatrix} [f(x)y∗]∼N([μfμy],[KffKfyTKfyKyy])
其中 K f f = κ ( x , x ) , K f y = κ ( x , x ∗ ) , K y y = κ ( x ∗ , x ∗ ) K_{ff}=\kappa(x,x),K_{fy}=\kappa(x,x^*),K_{yy}=\kappa(x^*,x^*) Kff=κ(x,x),Kfy=κ(x,x∗),Kyy=κ(x∗,x∗),则有 f ∼ N ( K f y T K f f − 1 y + μ f , K y y − K f y T K f f − 1 K f y ) f\sim\mathcal{N}(K_{fy}^TK_{ff}^{-1}y+\mu_f,K_{yy}-K_{fy}^TK_{ff}^{-1}K_{fy}) f∼N(KfyTKff−1y+μf,Kyy−KfyTKff−1Kfy)
上述式子表明了给定数据 ( x ∗ , y ∗ ) (x^*,y^*) (x∗,y∗)之后函数的分布 f f f仍然是一个高斯过程,具体的推导可见 Gaussian Processes for Machine Learning。这个式子可以看出一些有趣的性质,均值 实际上是观测点 的一个线性函数,协方差项 的第一部分是我们的先验的协方差,减掉的后面的那一项实际上表示了观测到数据后函数分布不确定性的减少,如果第二项非常接近于 0,说明观测数据后我们的不确定性几乎不变,反之如果第二项非常大,则说明不确定性降低了很多。
上式其实就是高斯过程回归的基本公式,首先有一个高斯过程先验分布,观测到一些数据(机器学习中的训练数据),基于先验和一定的假设(联合高斯分布)计算得到高斯过程后验分布的均值和协方差。
简单高斯过程回归实现
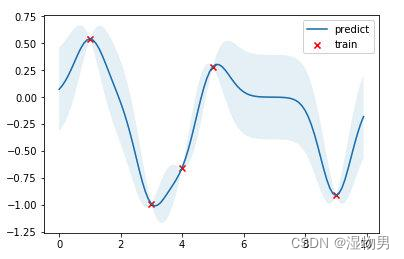
红点是训练数据,蓝线是预测值,浅蓝色区域是 95% 置信区间。真实的函数是一个 cosine 函数,可以看到在训练数据点较为密集的地方,模型预测的不确定性较低,而在训练数据点比较稀疏的区域,模型预测不确定性较高。
超参数优化
上文提到高斯过程是一种非参数模型,没有训练模型参数的过程,一旦核函数、训练数据给定,则模型就被唯一地确定下来。但是核函数本身是有参数的,比如高斯核的参数 σ \sigma σ和 l l l ,我们称为这种参数为模型的超参数(类似于 k-NN 模型中 k 的取值)。
核函数本质上决定了样本点相似性的度量方法,进行影响到了整个函数的概率分布的形状。上面的高斯过程回归的例子中使用了 σ = 0.2 , l = 0.5 \sigma=0.2,l=0.5 σ=0.2,l=0.5 的超参数,我们可以选取不同的超参数看看回归出来的效果。
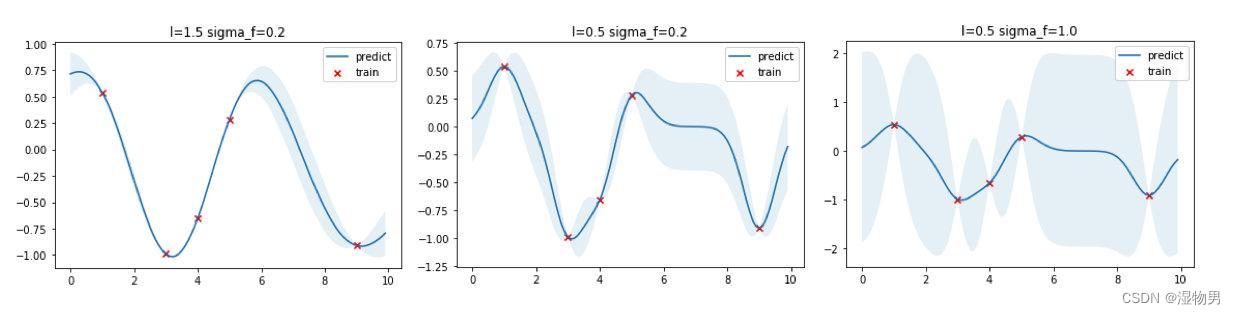
从上图可以看出, l l l越大函数更加平滑,同时训练数据点之间的预测方差更小,反之 l l l越小则函数倾向于更加“曲折”,训练数据点之间的预测方差更大; σ \sigma σ 则直接控制方差大小, σ \sigma σ 越大方差越大,反之亦然。
如何选择最优的核函数参数呢?答案是最大化在这两个超参数下 y y y 出现的概率,通过最大化边缘对数似然(Marginal Log-likelihood)来找到最优的参数,边缘对数似然表示为
l o g p ( y ∣ σ , l ) = l o g N ( 0 , K y y ( σ , l ) ) logp(y|\sigma,l)=log\mathcal{N}(0,K_{yy}(\sigma,l)) logp(y∣σ,l)=logN(0,Kyy(σ,l))
将训练、优化得到的超参数、预测结果可视化如下图,可以看到最优的