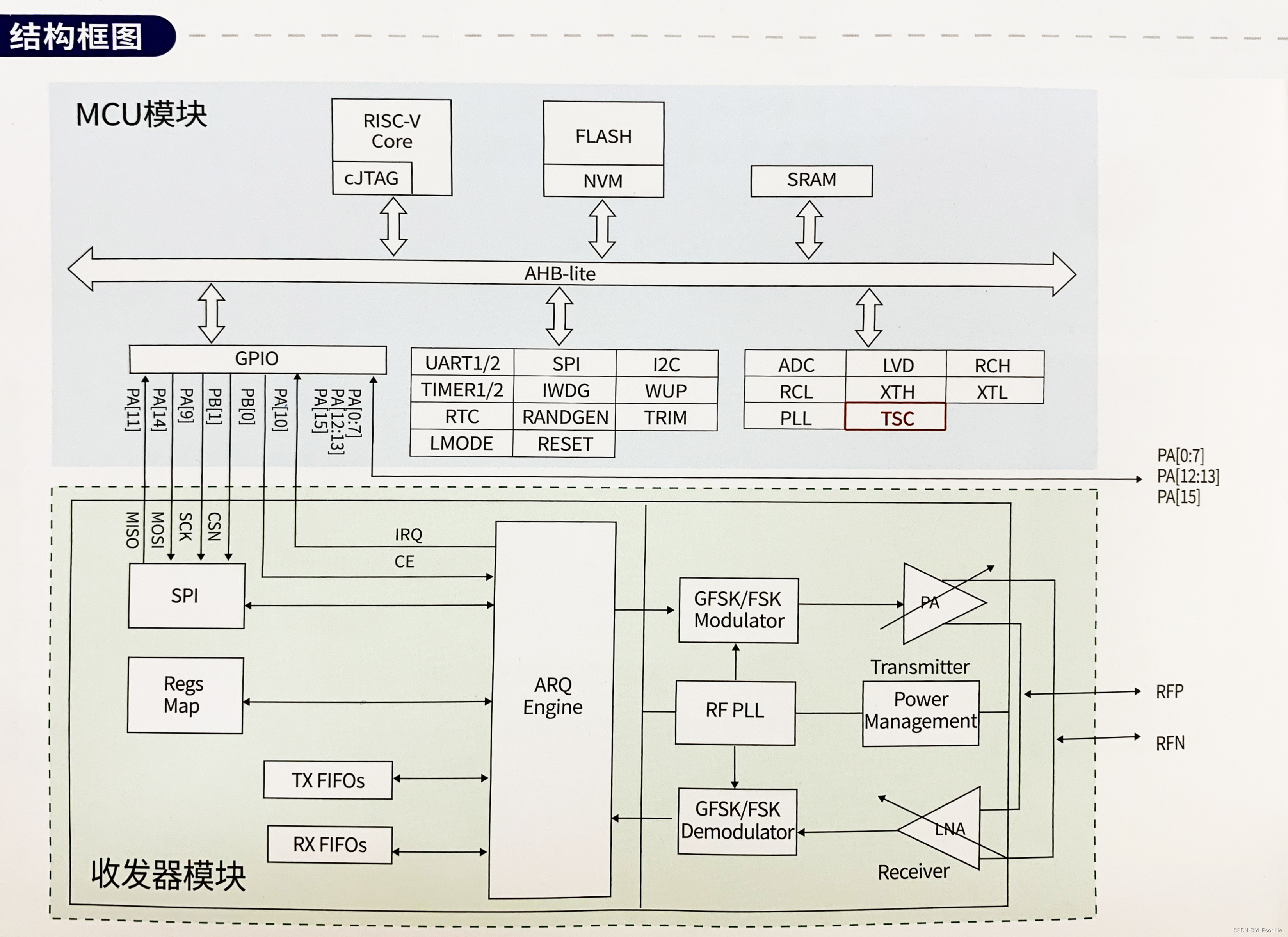
不同路径
- 重点:从左上角移动到右下角,m-1次向右,n-1次向下
- 题解1 DP
- 降维——滚动数组
- 题解2 求解组合 C m + n − 2 m − 1 C^{m-1}_{m+n-2} Cm+n−2m−1的值
一个机器人位于一个
m x n 网格的
左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
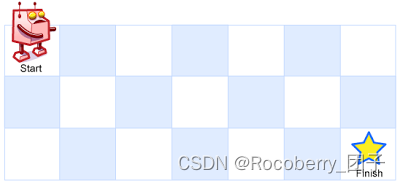
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
- 1 <=
m, n<= 100 - 题目数据保证答案小于等于 2 ∗ 1 0 9 2 * 10^9 2∗109
重点:从左上角移动到右下角,m-1次向右,n-1次向下
题解1 DP
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
// 必要的初始化
for(int i = 0; i < m; i++){
dp[i][0] = 1;
}
for(int i = 0; i < n; i++){
dp[0][i] = 1;
}
// 递推公式:dp[i][j] = dp[i-1][j] + dp[i][j-1] (只和i和i-1有关,可以用滚动数组优化)
for(int i = 1; i < m; i ++){
for(int j = 1; j < n; j++){
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};

降维——滚动数组
因为计算时,当前位置(i,j)的数据只和当前行的第j-1个数据和前一行的第j个数据有关,所以当计算当前行的第j个数据时,可以直接把上一行的第j个数据覆盖,不影响计算结果(即用第i行的数据逐渐覆盖第i-1行,不影响计算结果)。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> fn(n, 1);
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
fn[j] += fn[j-1];
}
}
return fn[n-1];
}
};

题解2 求解组合 C m + n − 2 m − 1 C^{m-1}_{m+n-2} Cm+n−2m−1的值
class Solution {
public:
int uniquePaths(int m, int n) {
long long ans = 1;
for (int x = n, y = 1; y < m; ++x, ++y) {
ans = ans * x / y;
}
return ans;
}
};






![[C++]3.类和对象下(this指针补充)+ 类和对象中构造函数和析构函数。](https://img-blog.csdnimg.cn/7e0c743553284382aa8a320c83fb4ab5.gif)