完全二叉树的节点个数

1. 递归普通二叉树遍历解法

   • 我们先来普及一下完全二叉树的概念：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

   • 这种解法是最简单在运行时间和速度空间上都很快，如果想不到完全二叉树的性质可以使用这种方法无脑遍历，无脑来解这道题。

   • 大概思路就是分别递归遍历左右节点直到节点为nil为止。

   • 由于代码思路很简单，我们直接看代码。

   type TreeNode struct {
     Val   int
     Left  *TreeNode
     Right *TreeNode
   }
   ​
   func countNodes(root *TreeNode) int {
     if root == nil {
       return 0
     }
     res := 1
     if root.Right != nil {
       res += countNodes(root.Right)
     }
     if root.Left != nil {
       res += countNodes(root.Left)
     }
     return res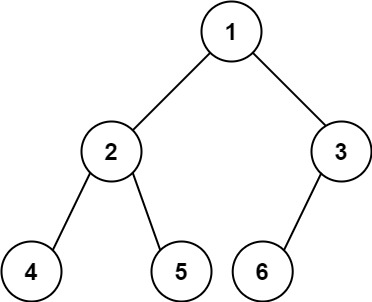
   }

   

使用普通二叉树的遍历方法的时间复杂度为On 这样的复杂度，还行！！！

1. 利用完全二叉树的特性来计算节点数量

   • 上面我们介绍了完全二叉树的特性：我们知道了一棵完全二叉树末尾节点只会从左边依次排开，不会出现右节点存在，左节点不存在的情况，所以我们利用这个特性，来遍历这个二叉树。

   • 假设存在满二叉树的情况，那么计算公式就为2h-1,所以我们只用判断最左边子二叉树的深度和最右边子二叉树的深度是否相等，如果相等就是满二叉树我们使用公式计算即可，如果不相等继续向下遍历。

   • 代码如下，虽然时间复杂度也是On但是当节点数量增多的时候会省去好多不必要的计算。

   type TreeNode struct {
     Val   int
     Left  *TreeNode
     Right *TreeNode
   }
   ​
   func countNodes(root *TreeNode) int {
     if root == nil {
       return 0
     }
     left := root.Left
     right := root.Right
     leftLight := 0
     rightLigh := 0
     for left != nil {
       left = left.Left
       leftLight++
     }
     for right != nil {
       right = right.Right
       rightLigh++
     }
     //满二叉树的情况
     if leftLight == rightLigh {
       return (2 << leftLight) - 1 //计算节点的数量
     }
     leftNumber := countNodes(root.Left)
     rightNumber := countNodes(root.Right)
     result := leftNumber + rightNumber + 1
     return result
   }