文章目录
- 前言
- AVL树的平衡性
- 不平衡的几种情况
- AVL树恢复平衡
- LL恢复平衡
- RR恢复平衡
- LR恢复平衡
- RL恢复平衡
- 总结
前言
上文对常见的数据结构进行了简单介绍,包括它们的定义、性质和特点。本文将对AVL树展开介绍,通过对AVL树的插入、删除、查找以及旋转操作全面掌握AVL树。
AVL树的平衡性
通过上文可以知道AVL树通过旋转操作解决二叉查找树可能成为线性结构的问题,也简单描述了左旋、右旋操作可以保持树的平衡。那么就有个问题:AVL树什么情况下进行左旋、右旋操作?
总的来说,当破坏树的平衡后需要左旋、右旋操作。什么时候会破坏?AVL树平衡性取决于左右子树高度差,也就是当插入或删除节点导致某个节点的左右子树高度差大于1时视为破坏树的平衡性,此时需要左旋、右旋操作来保持平衡。
不平衡的几种情况
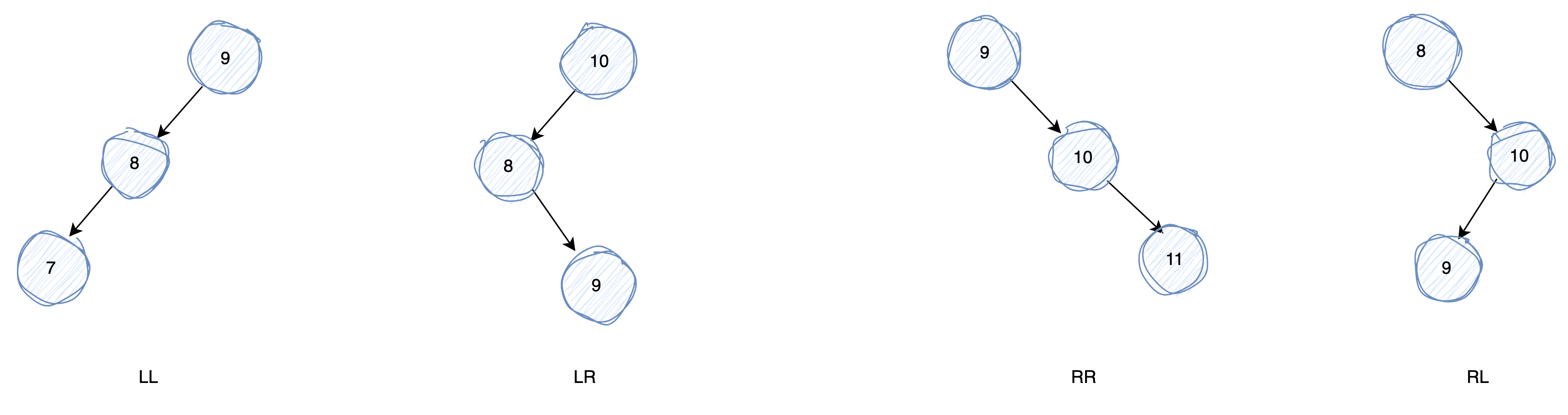
因为出现不平衡会有好几种情况,所以每个情况的旋转操作都是不一样的,下图为不平衡的几种情况。
-
LL:以上图为例,节点9的左子树高度为2且左子树也只有左子树,而右子树高度为0,两者高度差为2,大于1,破坏了树的平衡,这种情况称为LL。节点9需要进行一次右旋操作。
-
LR:以上图为例,节点10的左子树高度为2且左子树只有右子树,而右子树高度为0,两者高度差为2,大于1,破坏了树的平衡,这种情况称为LR。节点8需要先进行一次左旋操作后节点10再进行一次右旋操作。
-
RR:以上图为例,节点9的右子树高度为2且右子树也只有右子树,而左子树高度为0,两者高度差为2,大于1,破坏了树的平衡,这种情况称为RR。节点9需要进行一次左旋操作。
-
RL:以上图为例,节点8的右子树高度为2且右子树只有左子树,而右子树高度为0,两者高度差为2,大于1,破坏了树的平衡,这种情况称为RL。节点10需要先进行一次右旋操作后节点8再进行一次左旋操作。
AVL树恢复平衡
接下来演示这几种情况如何通过旋转操作恢复平衡的。
先复习一下:
右旋操作:以某个节点为旋转点,其左子节点变为其父节点,左子节点的右子节点变为其左子节点,右子节点不变。
左旋操作:以某个节点为旋转点,其右子节点变为其父节点,右子节点的左子节点变为其右子节点,左子节点不变。
LL恢复平衡
LL恢复平衡:一次右旋操作。
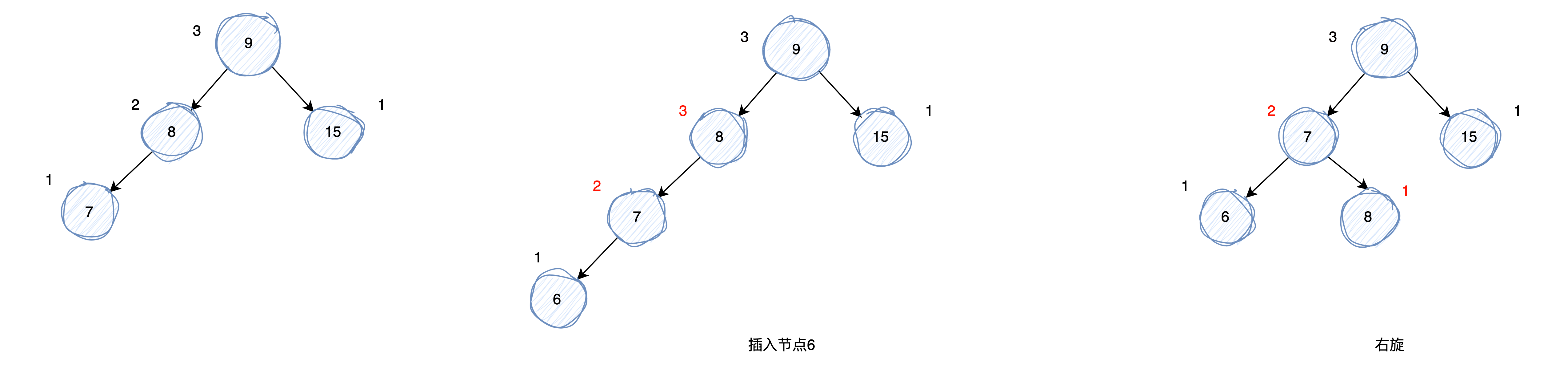
如上图,当插入节点6时,会向上更新节点的高度,当到达节点8时会发现其左子树高度为2,右子树为0,高度差为2,此时以节点8为旋转点向右旋转一次:节点7变为节点8的父节点,节点7的右子节点变为节点8的左子节点,节点8右子节点不变。示例代码如下:
private Node rotateRight(Node node) {
//节点7将作为父节点
Node newRoot = node.left;
//先将节点7的右子节点变为节点8的左子节点,这里因为没有,所以为null
node.left = newRoot.right;
//节点7变为节点8的父节点,因为是右旋,所以成为新父节点的右子节点
newRoot.right = node;
//更新节点高度
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
newRoot.height = Math.max(getHeight(newRoot.left), getHeight(newRoot.right)) + 1;
return newRoot;
}
RR恢复平衡
RR恢复平衡同LL。
LR恢复平衡
LR恢复平衡:一次左旋操作之后再一次右旋操作。

如上图,当插入节点6时,会向上更新节点的高度,当到达节点7时会发现其左子树高度为2,右子树为0,高度差为2,此时以节点5为旋转点向左旋转一次:节点6变为节点5的父节点,之后再以节点7为旋转点向右旋转一次,同上LL恢复平衡。示例代码如下:
private Node rotateRightAndLeft(Node node) {
//节点5左旋
node=rotateLeft(node.left);
//节点7右旋
node=rotateRight(node);
return node;
}
private Node rotateLeft(Node node) {
//节点6将作为父节点
Node newRoot = node.right;
//先将节点5的右子节点变为节点6的左子节点,这里因为没有,所以指向null
node.right = newRoot.left;
//节点6变为节点5的父节点,因为是左旋,所以成为新父节点的左子节点
newRoot.left = node;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
newRoot.height = Math.max(getHeight(newRoot.left), getHeight(newRoot.right)) + 1;
return newRoot;
}
RL恢复平衡
RL恢复平衡同LR。
总结
- AVL是一棵自平衡的查找二叉树。
- AVL的平衡性取决于某个节点的左右子树高度差是否大于1。
- 当插入或删除节点时可能会导致树的不平衡。
- 有4种不平衡的情况:LL、RR、LR、RL。
- 当出现不平衡的情况需要通过旋转节点保持平衡。
- LL:向右旋转一次。
- RR:向左旋转一次。
- LR:左子节点先左旋转一次,自己再向右旋转一次。
- RL:右子节点先右旋转一次,自己再向左旋转一次。