之前对于Tensor 的最好的定义：

需要注意的是：本文的一些内容使用的是非国际标准的符号，只是视频制作人的个人偏好。

如上图：张量是 使用张量积组合在一起的向量和协向量的集合。

所以，向量和协向量就像是所有其他张量的基本构建块，

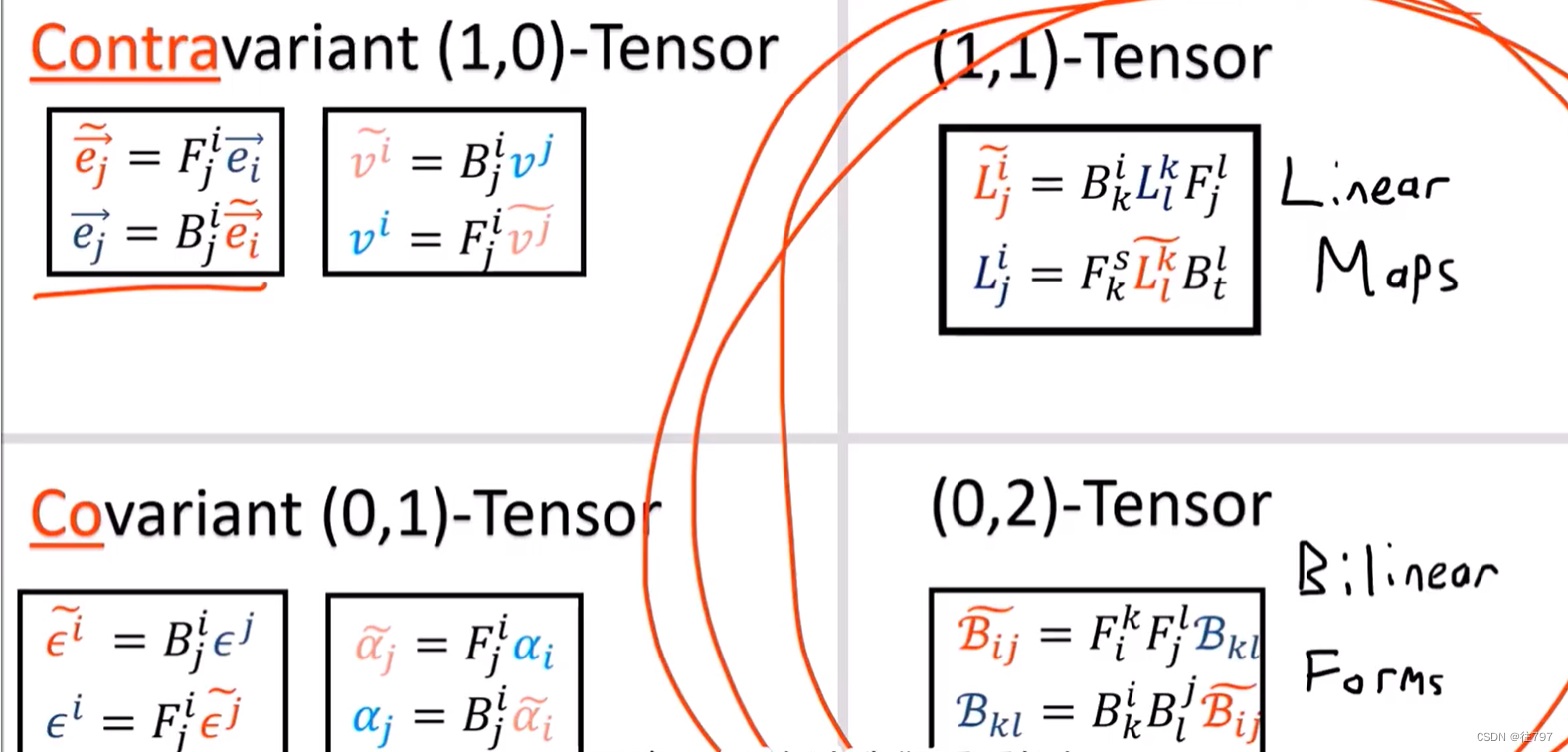
右边的两个张量，线性Map 和双线性形式 两个张量，如何用向量和协向量的乘积表示？

行*列= 标量 ； ；列*行 = Linear Map

 对于这个 Linear Map ，如何反过来求出它可由什么向量 和协向量表示?

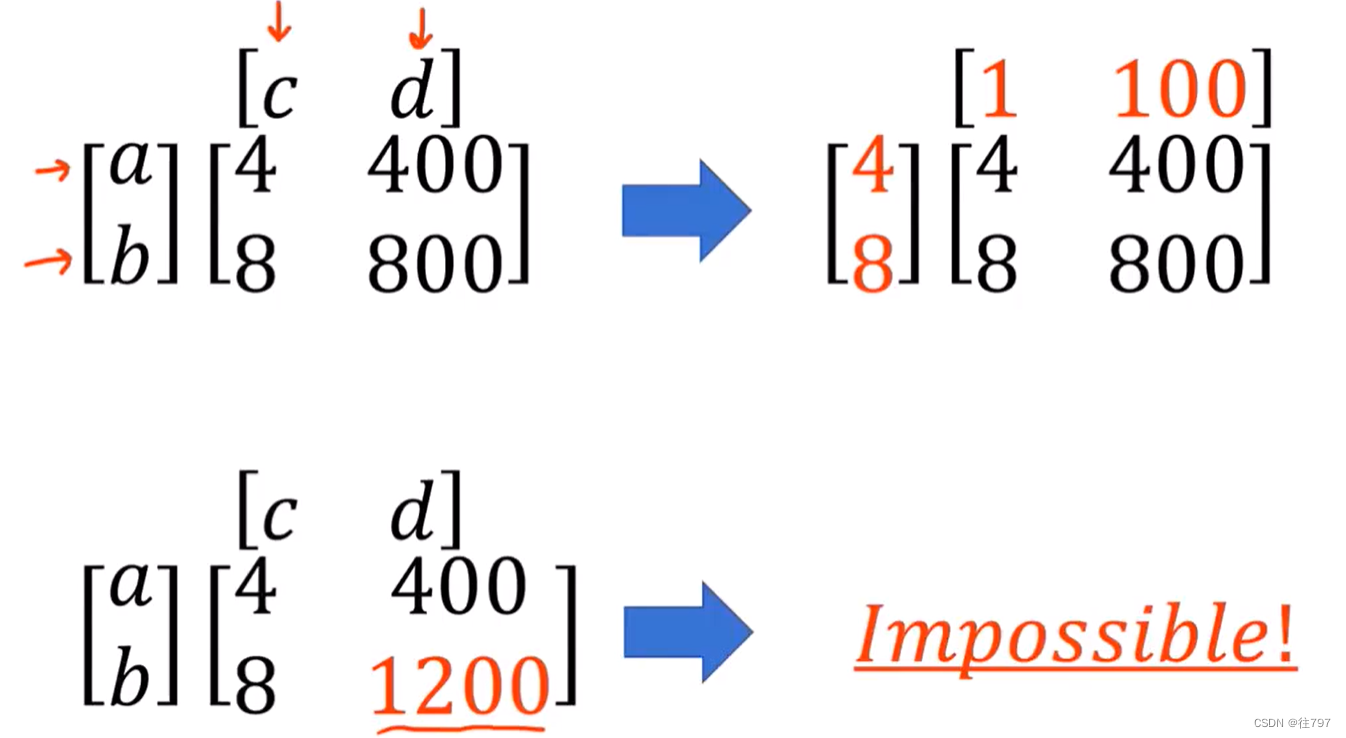
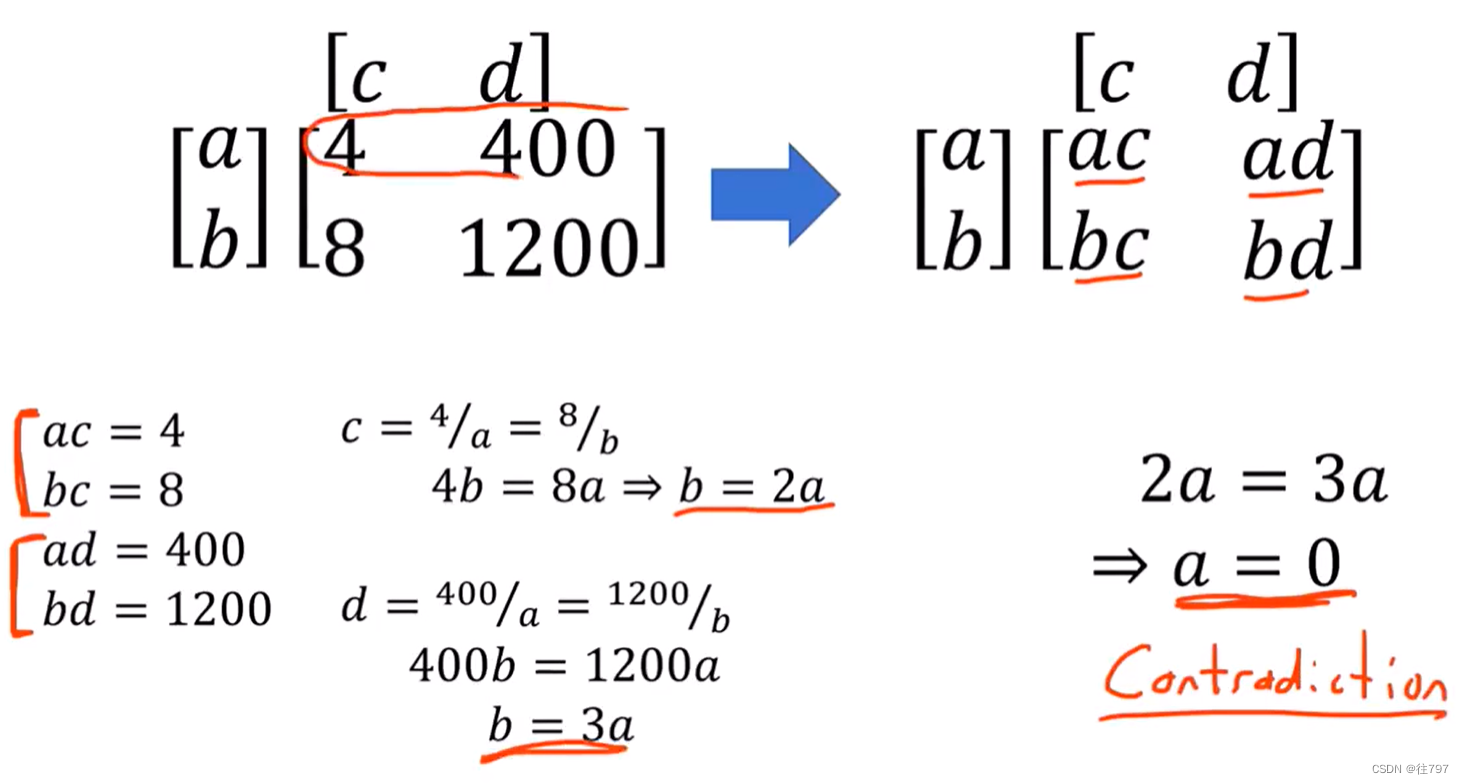
从上面可知， 有些矩阵可分为列*行(纯矩阵) ； 有些不可以（非纯矩阵）。

当纯矩阵用作线性映射时，其实很无聊， 因为所有的输出向量都沿着同一个方向存在。
而究其原因：对于纯矩阵，矩阵的列向量 都是彼此的标量倍数，

  ，  =  * 100 = 

   ,   =  * 2 = 

(矩阵列告诉我们每个基向量副本的去向，当它通过线性映射时，如果所有矩阵列都是彼此的倍数，。意味着，所有基向量都给出指向同一方向的输出。  这意味着通过线性映射的所有可能的矢量输入都被 发送到相同的方向， 这就是纯矩阵不太有趣的原因，它们可以做的转换集有限)

但非纯矩阵是更有趣的矩阵，它们可以将基向量发送到不同的方向，因此我们可以获得更有趣的转换。

不过有个问题， 我们可以用列向量*行向量积 构造出 纯矩阵，但它们是无聊的，
那么，如何使用列*行向量积 来构造 非纯矩阵？？

定义四个特殊的向量-协向量对，使用旧基ei，和旧对偶基εi ， 

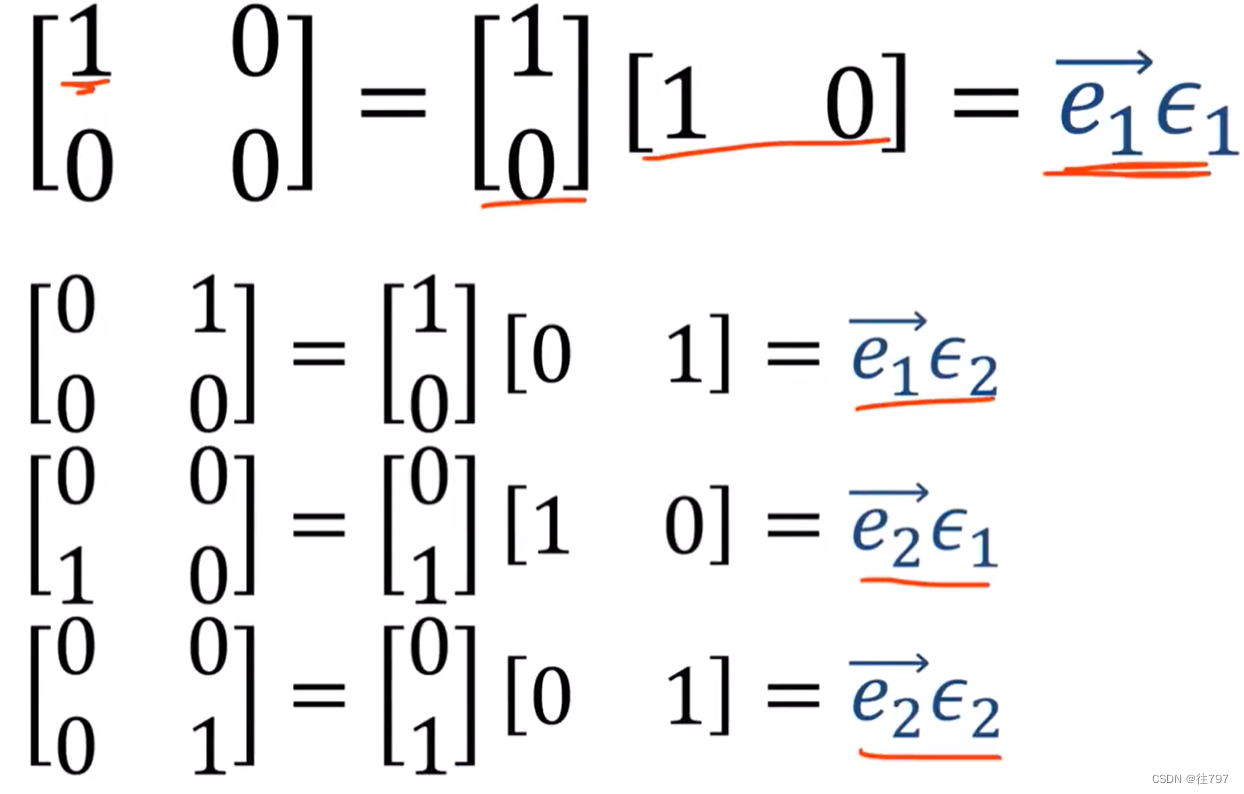
利用上面这四个矩阵进行线性组合，就能够构造出任意的二维矩阵，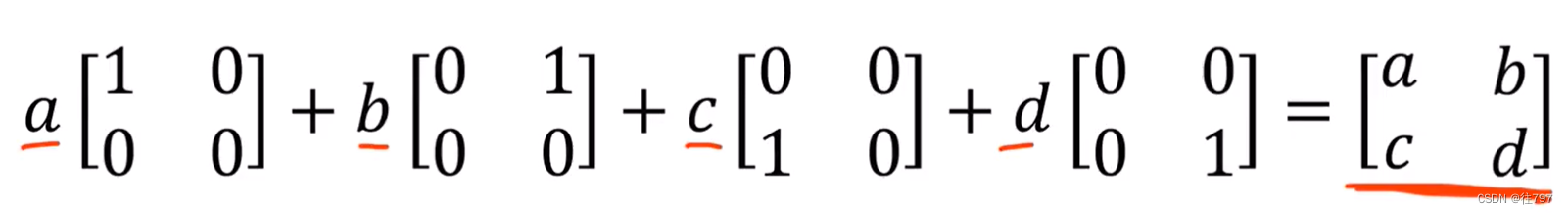

也就是说，可用下图这组四个乘积构成所有矩阵的基础，

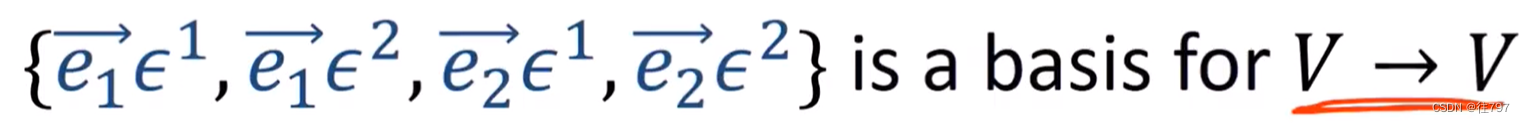
任何一般的线性映射L都可以写成下面这种线性组合

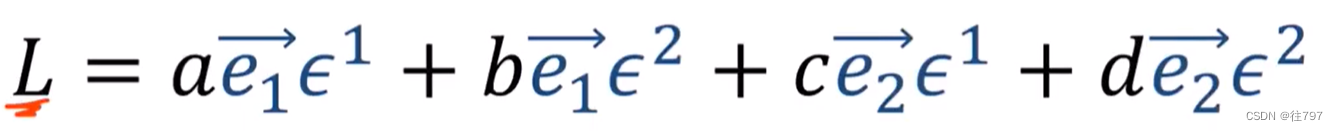
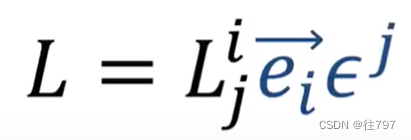
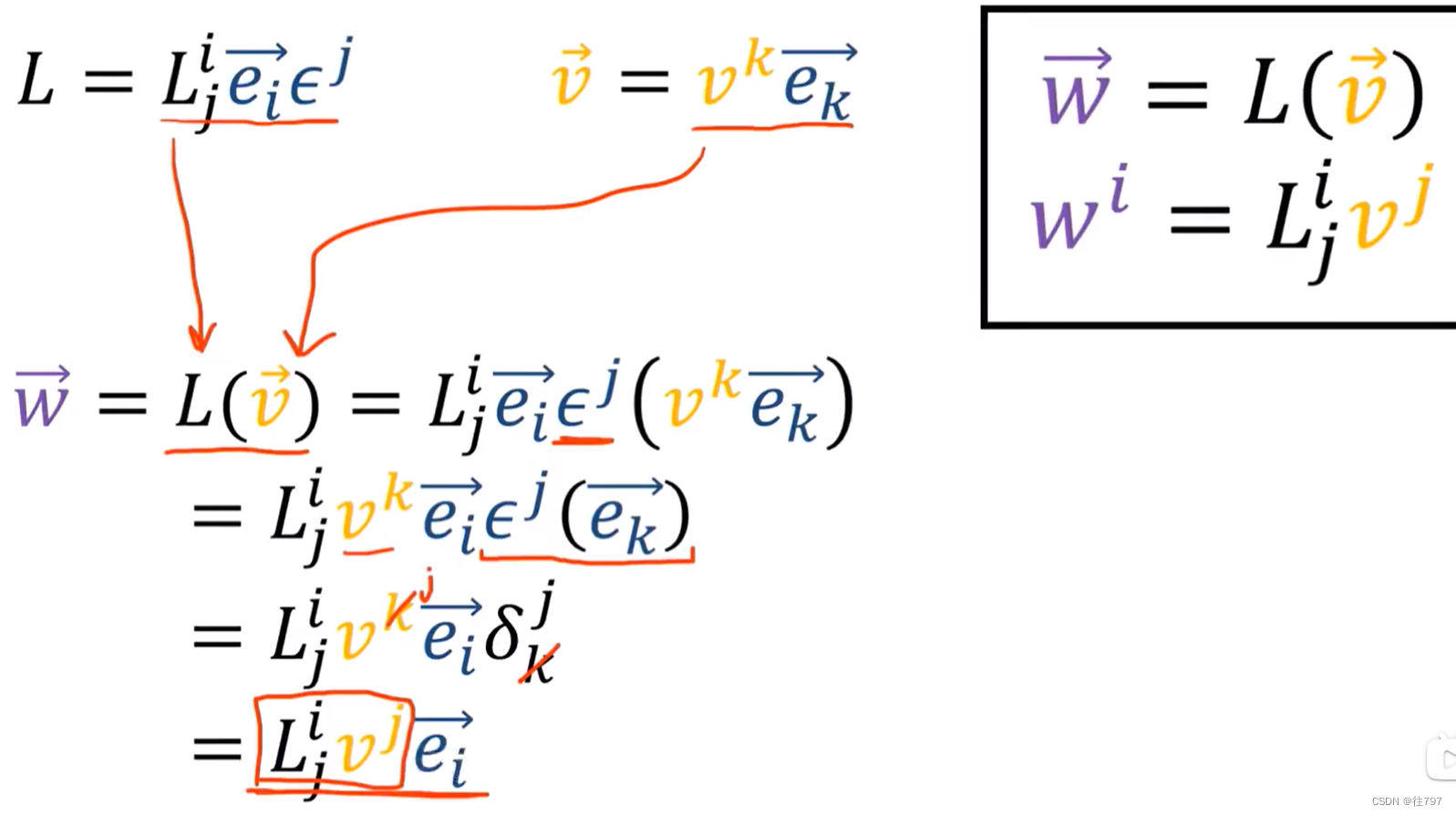
总结：

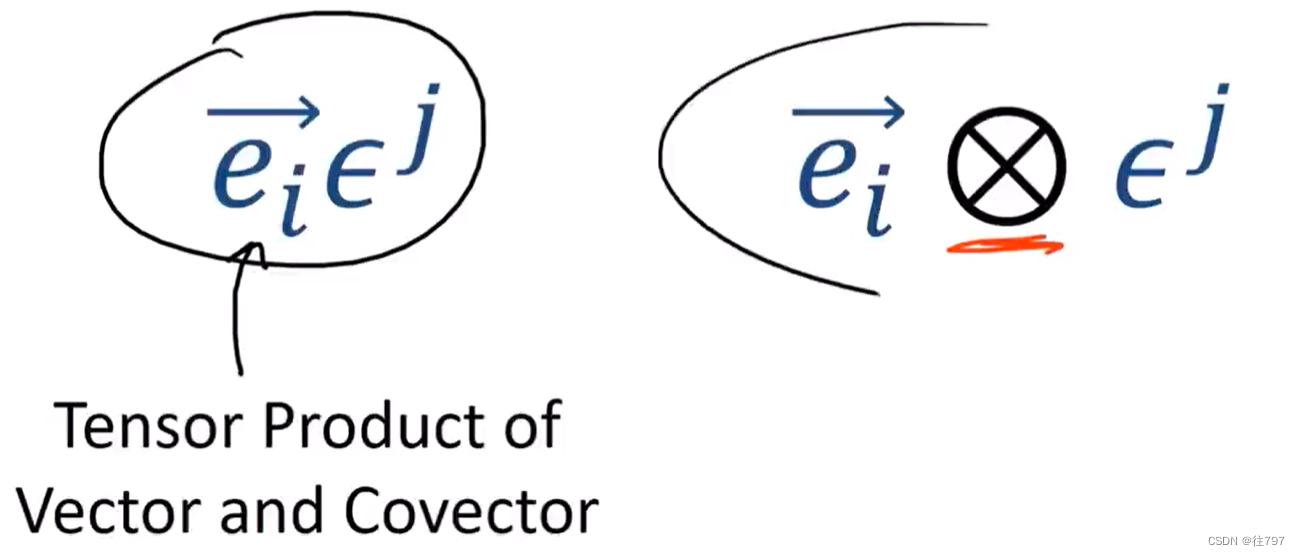
右边这个是标准形式。