Tensorboard
- 1. tensorboard 简单介绍
- 2. 安装必备环境
- 3. Tensorboard安装
- 4. 可视化命令
1. tensorboard 简单介绍
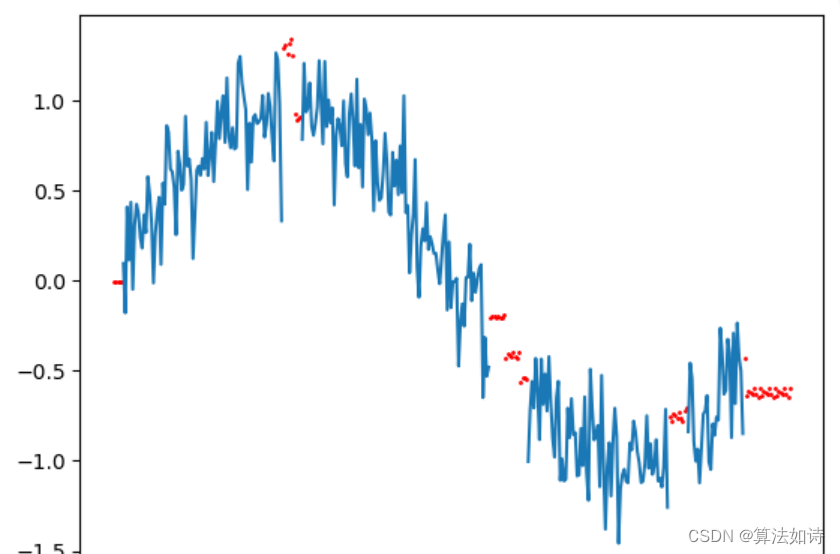
TensorBoard是一个可视化的模块,该模块功能强大,可用于深度学习网络模型训练查看模型结构和训练效果(预测结果、网络模型结构图、准确率、loss曲线、学习率、权重分布等)。
2. 安装必备环境
安装TensorBoard,必须要配一个带GPU的环境,tensorflow-gpu和pytorch的环境选一个就可以。
3. Tensorboard安装
pip install tensorboard
pip install tensorboardX
4. 可视化命令
运行命令后,选中生成的链接(如下图),打开可以看到可视化界面
tensorboard --logdir=<your_log_dir> --port=6007
<your_log_dir>是实验的日志路径
port参数为指定的端口号,可以不加,默认为6006
参考链接:
https://blog.csdn.net/Alexa_/article/details/131818209