提示：努力生活，开心、快乐的一天

---

647. 回文子串

题目链接：647. 回文子串

💡解题思路

1. 动规五部曲

• 确定dp数组以及下标的含义：在定义dp数组的时候 很自然就会想题目求什么，我们就如何定义dp数组。绝大多数题目确实是这样，不过本题如果我们定义，dp[i] 为 下标i结尾的字符串有 dp[i]个回文串的话，我们会发现很难找到递归关系。dp[i] 和 dp[i-1] ，dp[i + 1] 看上去都没啥关系。布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。
• 确定递推公式：主要就是两大情况： 就是s[i]与s[j]相等，s[i]与s[j]不相等这两种
  如果s[i]与s[j]不相等，dp[i][j]一定是false；
  如果s[i]与s[j]相等，这就复杂一些了，有如下三种情况
  情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
  情况二：下标i 与 j相差为1，例如aa，也是回文子串
  情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。result就是统计回文子串的数量

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        result++;
        dp[i][j] = true;
    }
}

• dp数组如何初始化：dp[i][j]初始化为false
• 确定遍历顺序：首先从递推公式中可以看出，情况三是根据dp[i + 1][j - 1]是否为true，在对dp[i][j]进行赋值true的。dp[i + 1][j - 1] 在 dp[i][j]的左下角，如图：
  所以遍历顺序是：要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的
• 举例推导dp数组：按照递推公式推导一下做推导，如果发现结果不对，就把dp数组打印出来
  因为dp[i][j]的定义，所以j一定是大于等于i的，那么在填充dp[i][j]的时候一定是只填充右上半部分。

🤔遇到的问题

1. 遍历顺序是从下到上，从左到右
2. dp[i][j]的定义与原来的不一样

💻代码实现

动态规划

var countSubstrings = function (s) {
    let len = s.length
    let res = 0
    let dp = new Array(len).fill(false).map(x => new Array(len).fill(false))
    for (let j = 0; j<len; j++) {
        for (let i = 0; i <=j; i++) {
            if (s[i] === s[j]) {
                if (j - i <= 1) {
                    dp[i][j] = true
                } else {
                    dp[i][j] = dp[i + 1][j - 1]
                }
                res += dp[i][j] ? 1 : 0
            }
        }
    }
    return res
};

🎯题目总结

动态规划的空间复杂度是偏高的，双指针法：
首先确定回文串，就是找中心然后向两边扩散看是不是对称的就可以了。
在遍历中心点的时候，要注意中心点有两种情况。
一个元素可以作为中心点，两个元素也可以作为中心点。
那么有人同学问了，三个元素还可以做中心点呢。其实三个元素就可以由一个元素左右添加元素得到，四个元素则可以由两个元素左右添加元素得到。
所以我们在计算的时候，要注意一个元素为中心点和两个元素为中心点的情况。

---

516. 最长回文子序列

题目链接：516. 最长回文子序列

💡解题思路

1. 动规五部曲

• 确定dp数组以及下标的含义：dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
• 确定递推公式：主要就是两大情况： s[i] 与 s[j]相同，s[i] 与 s[j]不相同
  如果s[i]与s[j]相同，dp[i][j] = dp[i + 1][j - 1] + 2
  如果s[i] 与 s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。加入s[j]的回文子序列长度为dp[i + 1][j]。加入s[i]的回文子序列长度为dp[i][j - 1]。那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
• dp数组如何初始化：
  首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。其他情况dp[i][j]初始为0就行，这样递推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖。
• 确定遍历顺序：从递归公式中，可以看出，dp[i][j] 依赖于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]
  所以遍历i的时候一定要从下到上遍历，这样才能保证下一行的数据是经过计算的。j的话，可以正常从左向右遍历。
• 举例推导dp数组：按照递推公式推导一下做推导，如果发现结果不对，就把dp数组打印出来
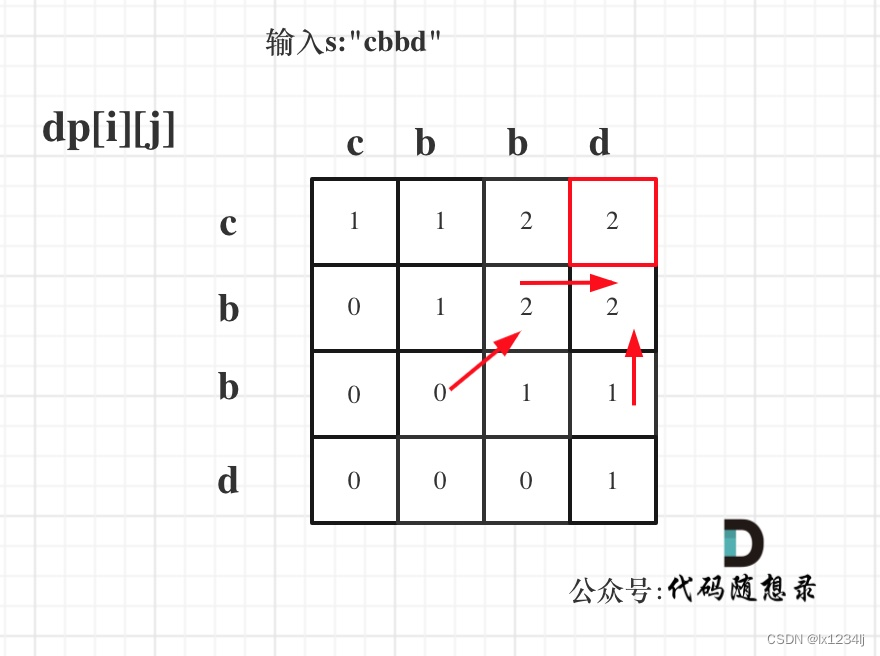
  红色框即：dp[0][s.size() - 1]; 为最终结果。

🤔遇到的问题

1. 别忘记初始化

💻代码实现

动态规划

var longestPalindromeSubseq = function(s) {
    let len = s.length
    let dp = new Array(len).fill(0).map(x => new Array(len).fill(0))
    for (let i = 0; i < len; i++){
        dp[i][i] = 1
    }
    for (let i = len - 1; i >= 0; i--){
        for (let j = i + 1; j < len; j++){
            if (s[i] === s[j]) {
                dp[i][j] = dp[i+1][j-1]+2
            } else {
                dp[i][j] = Math.max(dp[i][j-1],dp[i+1][j])
            }
        }
    }
    return dp[0][len-1]
};

🎯题目总结

时刻牢记dp[i][j]的含义
回文子串是要连续的，回文子序列可不是连续的！

🎈今日心得

动态规划基本完事啦，哈哈哈哈哈