近年来各个行业对超融合(Hyperconverged Infrastructure, 简称 HCI)的关注度越来越高,但各家厂商的超融合架构实现方法各有不同。我们在这里不评判对错,也不去探究这些是不是真正的超融合,而是重新追本溯源,思考为什么超融合现在被关注,什么样的 IT 架构更 “合适” 于当今的商业。
什么是超融合?
首先,关于什么是超融合,我们可以参考维基百科中的如下定义:
超融合基础架构(hyper-converged infrastructure)是一个软件定义的 IT 基础架构,它可虚拟化常见“硬件定义”系统的所有元素。HCI 包含的最小集合是:虚拟化计算(hypervisor),虚拟存储(SDS)和虚拟网络。HCI 通常运行在标准商用服务器之上。
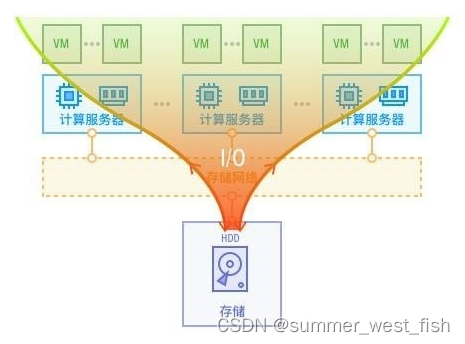
SmartX 选择超融合架构的原因,是传统存储解决不了现在企业数据中心的问题。据麦肯锡研究显示,全球的 IT 数据每年在以 40% 的速度增加中。数据正在逐步影响商业,企业通过数据的分析来做决策与管理。完成快速的分析决策和管理,就需要借助强大的数据中心。下图为传统 SAN 存储:
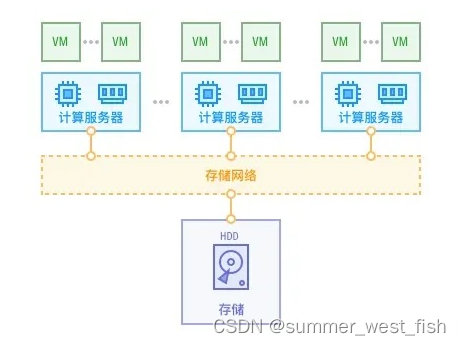
但是,光靠越来越快、核数越来越多的 CPU 是不够的,瓶颈在于传统存储的硬盘太慢了,CPU 大部分计算能力都空闲或者说在等待存储数据传输过来。传统存储容量和性能不具备和计算能力匹配的可扩展性,不能满足企业进行数据访问的需求。
这个问题并不是现在才有。Google 很早遇到这个问题。那么 Google 是如何做的呢?
作为一个给全世界互联网网民提供数据检索的企业,Google 考虑过 EMC、IBM,还有当年的 SUN 存储产品,但是都解决不了它的问题。无论是容量还是性能,这些公司的产品都无法满足 Google 的规模需求。于是 Google 只能自己建立一个适合自己的数据搜索的存储结构了。
Google 优秀的计算机科学家们,打破了传统的存储思维,利用服务器的本地硬盘和软件构建了一个容量和性能不断可扩展的分布式文件系统,并在其上构建了其搜索和分析的计算引擎。
不用把数据从存储端取出来,然后通过网络传输到计算端,而是将计算直接分发到存储上运行,将 “计算” 作为传输单元进行传输,这样大量的存储数据都是本地访问,不需要再跨网络上传输了,自然访问很快。于是乎,自然而然地,“计算” 和 “存储” 运行(“融合”)在了一个服务器上,这里也看到超融合架构的一个优势就是,本地访问数据,不必跨网络。
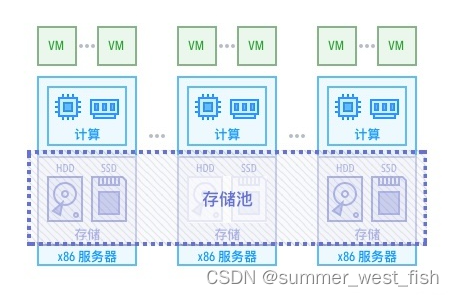
现代企业的数据量越来越大,应用越来越多,他们开始面临当年 Google 遇到的问题,CIO 要考虑怎么更高效的构建自己的计算和存储的基础架构,来满足应用的数据访问需求。
虚拟化为更容易的管理应用而生,它解决了 CPU、内存资源闲置的问题。但随着虚拟化的大规模应用,虚拟机越来越多,虚拟机在传统存储上运行却越来越慢了。“慢” 造成 “体验差”,“体验差” 成为了限制虚拟化应用的最大的瓶颈。这里面的最重要原因自然是,存储的 I/O 性能不够,大量的虚拟机和容器同时运行,I/O 的混合,使得随机读写急剧增加,传统存储的结构无法承受大量的随机 I/O。
超融合恰恰是为了解决这个问题,才被带到了虚拟化和容器领域。同时,业内也存在不同的解决 I/O 问题的方法,我们先尝试分析下其他的解决方法。
- 解决方法一:在存储设备采用 SSD 做 Cache,加速 I/O。这在一定的规模下可能有效,但是存储设备的 SSD Cache 通常比例较小,不足 5% 的容量比的情况下,自然满足不了用户的热数据的缓存需求。另外,仍然无法随需扩展,所有的数据仍然要从集中的存储控制器流出,这个集中的 “收费站” 势必堵塞 “高速公路”。
- 解决方法二:使用服务器侧 SSD 做 Cache,加速 I/O。这种类似的解决方案,通常缺乏高可靠性软件的支撑,服务器端的 Cache 如果用做写 Cache,存在单点失效的问题,需要在多个服务器的 Cache 设备上,做副本来提供可靠性,可以说这是一个阉割版的超融合架构,将 Cache 放到服务器端,仍然使用传统存储,当 Cache 满,需要被写回传统存储的时候,仍然被传统存储的 “控制器” 限制整体性能。
我们看到,上面的两种方案都是受限于传统存储的结构。超融合存储则不一样,通过完全去掉传统存储,利用分布式文件系统来提供 “不可限量” 的性能和容量,在这个基础上,再通过 Cache 进行加速,甚至全部使用闪存(全闪存产品)来构建都是自然而然,不被限制了。
因此,超融合架构不是为了让单台服务器的存储飞快,而是为了让每增加一台服务器,存储的性能就有线性的提升,这样的存储结构才不限制企业业务的运行,并保证业务的可靠性。
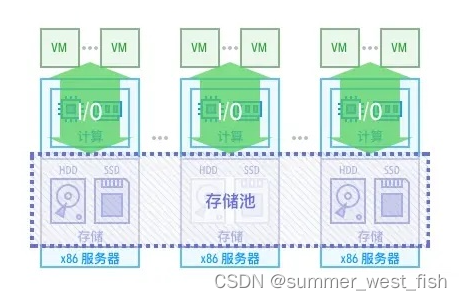
正因为这种扩展性很好的共享存储,使得整个 Google 的业务得以顺畅地运转。SmartX 在做的就是这样的更好的、更稳定的基础服务。
另外,超融合近几年得以快速发展的原因,这要归功于硬件设备。CPU 核数越来越多,服务器的内存容量越来越大,SSD 设备和网络互联网设备越来越快,这意味着:
- 服务器的资源除了运行业务以外,仍然可以预留出来足够的 CPU,内存资源来运行存储软件。将存储软件和业务运行到一块,既减少了设备量,减少了电力使用,本地读取也提高了 I/O 的存取效率。这在几年前是做不到的,因为 CPU 和内存太有限了。
- 网络互联越来越快,无论是万兆,40Gb 以太网,还是 Infiniband(无限宽带技术),使得我们的软件能够将独立的存储设备进行互连,通过分布式文件系统形成共享的存储池,供上层应用使用。
- 如果说 SSD 等硬件厂商让单个存储设备跑的更快,我们的软件的意义在于,让超大量的这些存储设备,一起工作,提供无止境的整体性能和容量。
上面我们阐述了传统存储对现代企业大量数据和随机 I/O 处理的表现乏力、超融合架构因何满足企业需求以及超融合架构得以快速发展的原因。
下面将进一步解释在超融合架构中,层次存储为什么是提升数据的 I/O 性能的最好选择。
首先,让我们追溯到现代计算机体系结构中,解决系统性能瓶颈的关键策略:Cache。
现代计算机体系结构是基于冯·诺依曼体系结构构建的,冯 · 诺依曼体系结构将程序指令当做数据对待,程序和数据存储在相同的存储介质(内存)中,CPU 通过系统总线从内存中加载程序指令和相应的数据,进行程序的执行。
冯 · 诺依曼体系结构解决了计算机的可编程性问题,但是带来了一个缺点,因为程序指令和数据都需要从内存中载入,尽管 CPU 的速度很快,却被系统总线和内存速度的限制,不能快速的执行。为解决这个问题,Cache 的理念被提出,通过在 CPU 和内存之间加入更快速的访问介质(CPU Cache),将 CPU 经常访问的指令和数据,放置到 CPU Cache 中,系统的整体执行速度大幅度提升。
I/O 性能瓶颈问题转移到了存储
如果内存的访问速度相对 CPU 太慢,那么磁盘的 I/O 访问速度相对 CPU 来说就是 “不能忍” 了。下表是不同存储介质的访问延时,在虚拟化环境下或云环境下,由于 I/O 基本都是随机 I/O,每次访问都需要近 10ms 的寻道延时,使得 CPU 基本处于 “等待数据” 的状态,这使得核心业务系统运转效率和核心应用的用户体验都变得很差,直观的感受就是业务系统和桌面应用 “很卡”。

基于 SSD 构建平衡系统
和前人解决内存访问延时问题的思路类似,现在的主流方法是使用内存和 SSD 作为 Cache 来解决 I/O 性能瓶颈。存储系统能够分析出数据块的冷热程度,将经常访问的数据块缓存到内存和 SSD 中,从而加速访问。
不论是全闪存存储,还是混合介质存储,从某种意义上讲都是层次存储,只不过混合阵列多了一层磁盘介质。
学过计算机体系结构的人都听说过著名的 Amdahl 定律,这里我们要介绍一个 Amdahl 提出的 “不那么著名” 的经验法则:
在一个平衡的并行计算环境中,每 1GHz 的计算能力需要 1Gbps 的 I/O 速度与之匹配。
假设一台服务器有 2 颗 E5-4669 v3 的 CPU,每颗 CPU 有 18 个核,36 个超线程,主频是 2.1GHz,那么我们可以计算一下,这样的一台服务器需要 151Gbps (即~19GBps)的带宽。
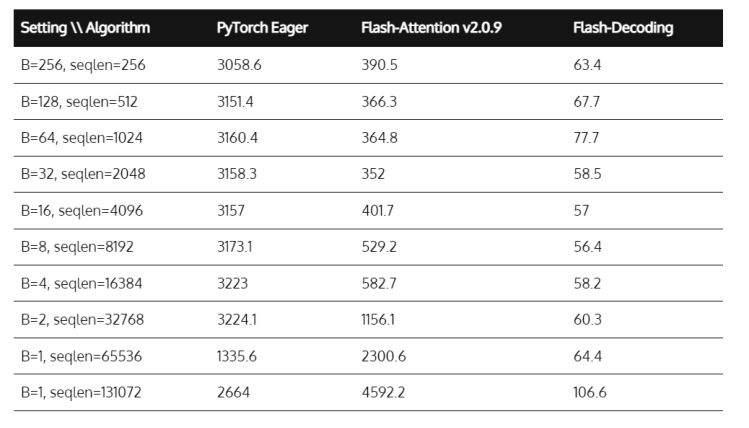
在大规模的云计算(虚拟机算)环境中,极端情况下,大量的 I/O 并发使得存储收到的 I/O 都变成随机 I/O,在这么一个并发环境中,假设我们的访问大部分都是 8KB 的读写,根据上面的计算,我们需要为一台服务器配备近 250 万的 IOPS 读取速度。
在不考虑系统总线的情况下,如果我们用 SAS/SATA 硬盘来提供这个 IOPS,即使每个 SAS/SATA 盘可以提供近 250 的 IOPS(实际数值更小),仅为构建一台平衡的服务器计算存储环境,就需要大概 1 万个 SAS/SATA 硬盘。
在稍大规模的虚拟化环境,想要搭出一个平衡的系统,用传统的 SAS/SATA 硬盘几乎不可能完成任务。但是如果采用能够提 10 万 “写 IOPS” 的 SSD 设备,25 块 SSD 就够了。
层次存储的优势
“层次存储” 是相对 “全闪存” 而言,是指将容量大但是速度较慢的 HDD 和速度快的 SSD 同时构建在系统中,通过数据的访问特性,将经常访问的热数据放置在 SSD 中,而冷数据放置在 HDD 中。
首先,为构建一个平衡的虚拟化环境,需要大量的 SSD 设备来提供足够的 IOPS。但是 SSD 也不是完美的。目前的 SSD 擦写次数有限、价格高。层次存储将热数据放置在 SSD 层中,而大量的冷数据仍然放置在 SATA 硬盘上,热数据周期性的同步到 HDD 硬盘,既为用户热数据提供了高 IOPS 的保障,也通过 SATA 硬盘提供了更大的容量和可靠性。
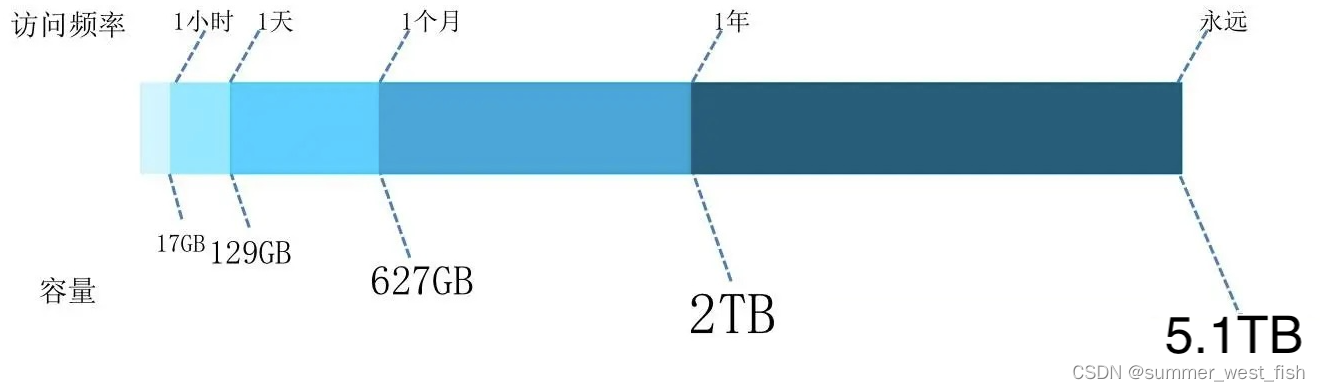
下图是对 11 个开发人员桌面负载的 I/O 统计,包含了对 5.1TB 大小的存储上的 76 亿次 IO 访问和 28TB 的数据传输。首先值得注意的是,有 3.1TB (62%) 的数据,在一年内从来没有被访问过,这意味着这些数据无论是放置在 SSD 上,还是 SATA 上,甚至放到 U 盘上拔走,对系统都没有影响。