问题研究背景
使用遗传模拟退火算法求解如下10个卸货点的VRPTW问题。为了使研究的问题更加有意义,本人将时间限理解为服务点一天的具体可以允许配送的时间。 如果不要求车辆从配送中心出发的时间是统一的并且为0时刻,那么就默认第一个配送节点是一定能赶到的。采取从配送中心出发的时间不为0时刻的策略,默认一定能达到第一个配送点,所以采用最早到达时间推算车辆出发的时间。
假设配送中心营业时间是早上七点至晚上七点,即配送中心也有最早和最晚时间窗要求,车辆配送货物应该满足这个发车即回到配送中心的最晚时间限制。卸货点1-10的时间限制理解如下:卸货点1要求在下午1点至下午4点配送,卸货点1要求的服务时间是半个小时;卸货点2要求在下午4点至下午6点配送,卸货点2要求的服务时间是1个小时,以此类推其他的卸货点的配送及服务时间限制。算法中用到配送及服务时间是下午的情况,例如卸货点1可转成数字表示是[13,16]。
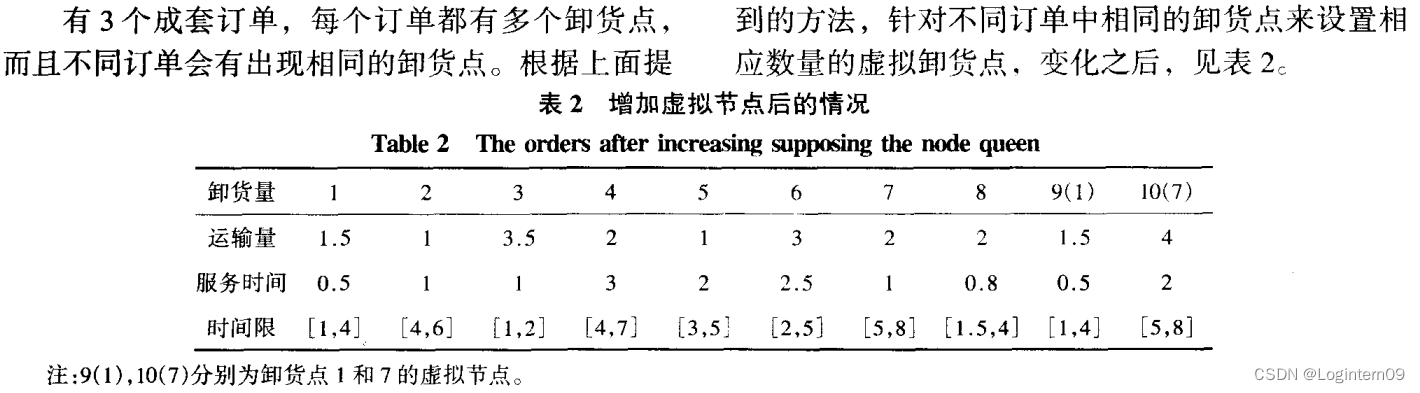
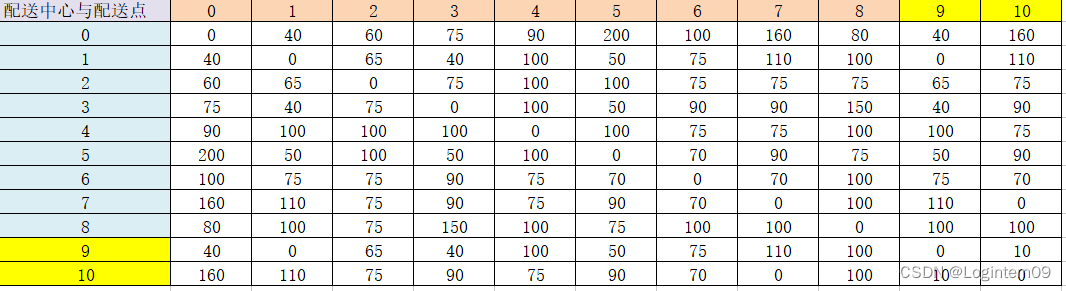
配送点的需求货物量如下:

配送点的达到时间窗及服务时间如下:

代码编码思路
取染色体,依次判断染色体的基因是否满足车辆载重量及时间窗限制条件,染色体基因片段如果不满足两者,则默认为一条路线,在中间插入配送中心节点0.
考虑是否可以写两个独立的函数,先判断车辆的载重量限制,再前面生成的解再次寻优判断是否满足时间窗限制。
编写代码过程中遇到的错误
从配送中心出发立即回到配送中心
chrom [10 1 5 2 3 6 4 9 7 8]
*******000******
*******000******
routes [[0, 0, 0]]
当首次配送的需求点为卸货点10时,最早到达时间要求是下午5点,配送中心开门是上午七点,关门是下午七点,两点之间的路径长度是160公里,车辆每小时的车速是40公里/小时,所以最佳的方案是不考虑先去卸货点10完成配送任务,因为车辆返回时赶不上配送中心的关门时间。
一些其他的错误
opulation [[ 7 6 1 2 9 3 4 5 8 10]
[ 3 2 5 10 7 4 6 8 1 9]
[ 4 6 8 7 1 9 5 3 2 10]
[10 5 7 2 6 4 3 9 8 1]
[ 9 7 10 8 2 1 4 5 3 6]
[ 5 10 9 3 6 1 2 4 8 7]
[ 5 6 2 7 3 10 9 4 8 1]
[ 2 9 1 3 10 8 6 4 5 7]
[ 7 3 1 6 2 10 9 8 4 5]
[10 4 5 9 6 7 3 2 1 8]
[ 2 4 3 5 8 6 7 1 10 9]
[ 9 2 6 8 3 1 5 4 10 7]
[10 2 9 5 1 4 6 3 8 7]
[ 4 9 5 2 6 1 10 3 8 7]
[ 7 4 6 8 9 10 3 2 1 5]
[10 1 4 9 6 2 3 5 7 8]
[10 9 5 4 3 2 8 1 7 6]
[ 7 3 8 1 10 5 4 2 9 6]
[ 3 9 10 4 6 7 5 2 1 8]
[ 5 10 3 6 4 7 9 1 2 8]
[ 5 7 3 6 1 2 4 9 10 8]
[ 3 9 1 10 5 4 2 7 6 8]
[10 7 1 2 5 8 6 9 4 3]
[10 6 8 2 9 7 4 5 1 3]
[ 4 2 7 1 9 3 10 5 8 6]
[ 7 4 5 8 1 3 9 6 10 2]
[ 4 1 7 5 9 2 3 10 8 6]
[ 5 3 1 10 8 9 7 6 4 2]
[ 7 3 4 5 9 6 8 1 10 2]
[ 4 2 5 10 1 9 6 7 8 3]
[ 1 6 4 2 10 7 3 8 9 5]
[ 9 4 3 6 8 10 2 1 7 5]
[ 4 7 2 3 9 10 1 5 6 8]
[ 5 6 10 8 9 7 2 1 3 4]
[ 8 3 9 1 6 5 4 10 7 2]
[ 5 7 4 9 3 8 10 1 2 6]
[ 7 2 9 1 6 5 4 10 3 8]
[ 6 10 4 5 8 7 1 3 9 2]
[ 9 5 10 8 3 6 7 2 1 4]
[ 5 6 3 10 4 9 8 7 1 2]
[ 7 1 8 6 2 3 9 5 10 4]
[ 9 1 8 7 4 3 2 6 10 5]
[ 7 3 2 10 1 6 4 9 8 5]
[ 5 9 6 3 7 2 8 4 1 10]
[ 1 2 4 7 8 5 3 6 9 10]
[ 3 7 2 1 6 10 5 9 4 8]
[ 7 5 9 3 8 4 10 2 1 6]
[ 5 6 8 10 9 3 7 4 1 2]
[ 3 9 7 6 5 2 10 1 4 8]
[ 3 4 2 7 1 9 8 5 10 6]]
chrom [ 7 6 1 2 9 3 4 5 8 10]
*******000******
total_path_list [[0, 7, 6, 0], [0, 1, 2, 9, 0], [0, 3, 0], [0, 4, 5, 8, 0], [0, 10, 0]]
node 2
node 3
new_chrom [2, 3, 0, 9, 0, 0]
*******000******
total_path_list [[0, 0, 9, 0]]
new_chrom [9]
*******000******
total_path_list [[0, 9, 0]]
node 9
new_chrom [9]
routes [9]
cannotbe_firstnode_served [4, 5, 7, 10]
*******000******
total_path_list [[0, 5, 1, 2, 0], [0, 10, 0], [0, 4, 6, 0], [0, 3, 0], [0, 7, 8, 0], [0, 9, 0]]
path_list [0, 5, 1, 2, 0]
path_list [0, 10, 0]
path_list [0, 4, 6, 0]
path_list [0, 3, 0]
path_list [0, 7, 8, 0]
path_list [0, 9, 0]
new_chrom [3, 9, 5, 10, 4, 7]
*******000******
total_path_list [[0, 10, 0], [0, 4, 0], [0, 5, 0], [0, 7, 0]]
total_path_list [[0, 2, 3, 0], [0, 4, 5, 0], [0, 6, 7, 0], [0, 8, 9, 0], [0, 10, 0], [0, 1, 0]]
path_list [0, 2, 3, 0]
path_list [0, 4, 5, 0]
path_list [0, 6, 7, 0]
path_list [0, 8, 9, 0]
path_list [0, 10, 0]
path_list [0, 1, 0]
feasible_node_list [2, 3, 6, 8, 9, 1]
not_feasible_node_list [4, 5, 7, 10]
new_chrom [2, 3, 6, 8, 9, 1, 4, 5, 7, 10]
Process finished with exit code 0
函数代码
修改卸货点的时间窗,增加求得时间窗+车辆载重量约束限制的可行解概率。

车辆容量限制的代码见本博主的博文《【纠错】遗传算法求解VRP计算车辆容量限制的代码有bug》,时间窗要求的函数如下:
def time_window_restraint(total_path_list):
# 先求解车辆容量限制,再计算时间窗限制,硬时间窗限制
# 如果不要求车辆从配送中心出发的时间是统一的并且为0时刻,那么就默认第一个配送节点是一定能赶到的
# 采取从配送中心出发的时间不为0时刻的策略,默认一定能达到第一个配送点,所以采用最早到达时间推算车辆出发的时间
# 假设配送中心营业时间是早上七点至晚上七点
# 先排除算例无解的场景,即配送中心开门时间都不能实现派车辆运输的场景
print("total_path_list", total_path_list)
not_feasible_node_list = []
feasible_node_list = []
feasible_path_list = []
for i in range(len(total_path_list)):
path_list = total_path_list[i]
arrive_time = demand_time_window[0, path_list[1]]
leave_time = arrive_time + demand_service_time[path_list[1]]
if path_list[1] in cannotbe_firstnode_served:
not_feasible_node_list.extend(path_list[1:-1])
else:
# 默认第一个服务点的时间窗一定是满足要求的
if len(path_list) == 3:
# 返回配送中心的时间
back_center_time = leave_time + travel_time_graph[path_list[-2]][0]
if back_center_time > dis_center_open_time[1]:
not_feasible_node_list.append(path_list[-2])
else:
# 只有一个配送节点的场景
feasible_node_list.append(path_list[-2])
else:
feasible_node_list.append(path_list[1])
if len(path_list) == 4:
before_node = path_list[1]
cur_node = path_list[2]
arrive_time = leave_time + travel_time_graph[before_node][cur_node]
if (arrive_time < demand_time_window[0, cur_node]) or (arrive_time > demand_time_window[1, cur_node]):
# 不可行解
# 判断是否加入不可行解集合
if before_node in feasible_node_list:
feasible_node_list.remove(before_node)
not_feasible_node_list.append(before_node)
not_feasible_node_list.append(cur_node)
else:
not_feasible_node_list.append(cur_node)
else:
leave_time = arrive_time + demand_service_time[cur_node]
# 返回配送中心的时间
back_center_time = leave_time + travel_time_graph[cur_node][0]
if back_center_time > dis_center_open_time[1]:
# 判断是否加入不可行解集合
if before_node in feasible_node_list:
feasible_node_list.remove(before_node)
not_feasible_node_list.append(before_node)
not_feasible_node_list.append(cur_node)
else:
not_feasible_node_list.append(cur_node)
else:
# 判断是否加入可行解集合
if before_node in not_feasible_node_list:
not_feasible_node_list.append(cur_node)
else:
feasible_node_list.append(cur_node)
else:
remain_node_list = path_list[2:-1]
for index in range(len(remain_node_list)):
cur_node = remain_node_list[index]
if len(remain_node_list) == 1:
before_node = remain_node_list[0]
else:
before_node = remain_node_list[index-1]
arrive_time = leave_time + travel_time_graph[before_node][cur_node]
if (arrive_time < demand_time_window[0, cur_node]) or (
arrive_time > demand_time_window[1, cur_node]):
# 不可行解
# 判断是否加入不可行解集合
if before_node in feasible_node_list:
feasible_node_list.remove(before_node)
not_feasible_node_list.append(before_node)
not_feasible_node_list.append(cur_node)
else:
not_feasible_node_list.append(cur_node)
else:
leave_time = arrive_time + demand_service_time[cur_node]
if cur_node == path_list[-2]:
# 返回配送中心的时间
back_center_time = leave_time + travel_time_graph[path_list[-2]][0]
if back_center_time > dis_center_open_time[1]:
# 判断是否加入不可行解集合
if before_node in feasible_node_list:
feasible_node_list.remove(before_node)
not_feasible_node_list.append(before_node)
not_feasible_node_list.append(cur_node)
else:
# 判断是否加入可行解集合
not_feasible_node_list.append(cur_node)
else:
# 判断是否加入可行解集合
if before_node in not_feasible_node_list:
not_feasible_node_list.append(cur_node)
else:
feasible_node_list.append(cur_node)
else:
# 判断是否加入可行解集合
if before_node in not_feasible_node_list:
not_feasible_node_list.append(cur_node)
else:
feasible_node_list.append(cur_node)
new_chrom = []
if len(feasible_node_list) > 0:
for node in feasible_node_list:
new_chrom.append(node)
if len(not_feasible_node_list) > 0:
for node in not_feasible_node_list:
new_chrom.append(node)
not_feasible_node_flag = True
else:
not_feasible_node_flag = False
print("new_chrom", new_chrom)
return not_feasible_node_flag, feasible_node_list, new_chrom
def get_feasible_route(chrom):
# 先判断是否满足车辆最大载重量限制
cur_chrom = copy.deepcopy(chrom)
not_feasible_node_flag = True
count = 0
while not_feasible_node_flag:
# 先用得到满足车辆载重量的函数切出可行解路径
print("*******000******")
total_path_list = vehicle_capacity_restraint(cur_chrom)
# 再使用时间窗判断是否路径也是满足时间窗要求的
not_feasible_node_flag, feasible_node_list, new_chrom = time_window_restraint(total_path_list)
print("not_feasible_node_flag", not_feasible_node_flag)
if not_feasible_node_flag:
print("*******001******")
cur_chrom = new_chrom
count += 1
else:
print("*******003******")
return vehicle_capacity_restraint(new_chrom)
if (count > 1) and (cur_chrom == new_chrom):
return vehicle_capacity_restraint(new_chrom) # 使用函数切出路线
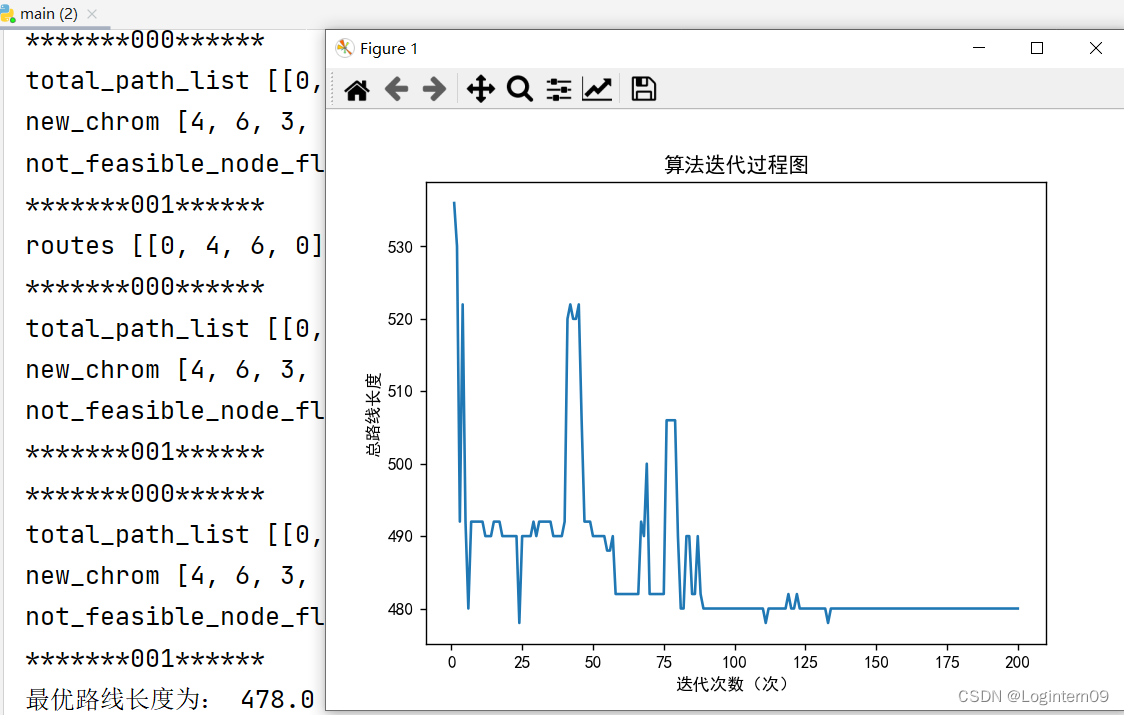
算法迭代示意图
遗传算法迭代图如下:
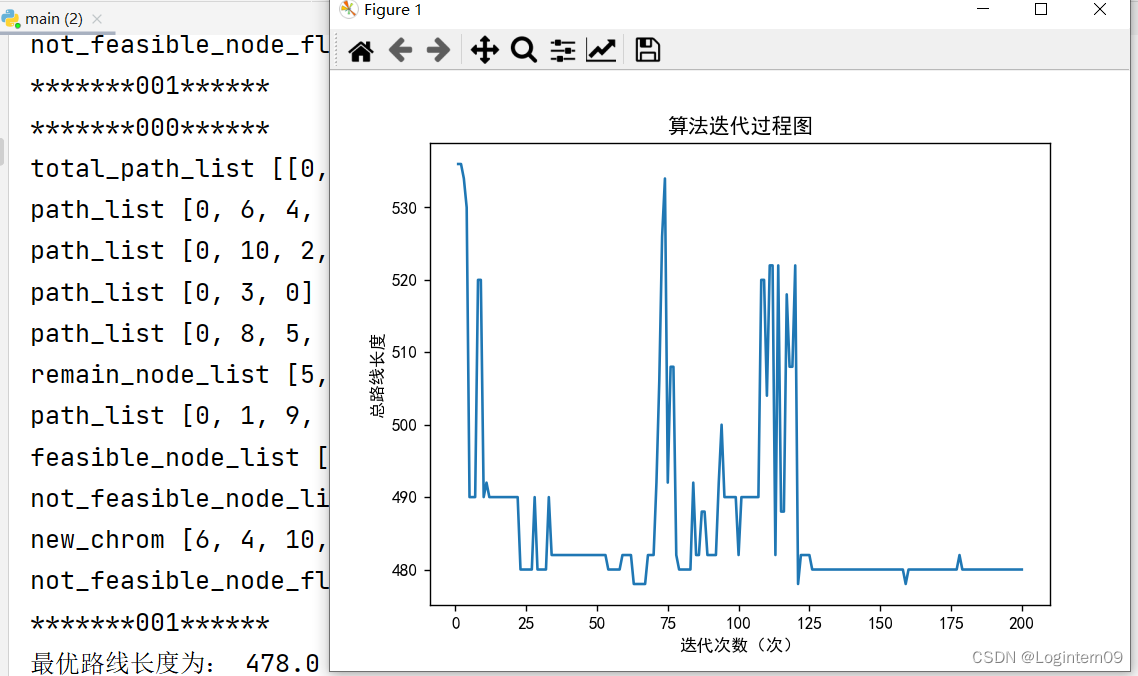
连续两次运行程序,得到的目标值相同,下面图2比上图1在100代左右就寻找到了结果:

事不过三,连续三次,目标值开出来的都是478