目录
1.算法效率
1.1.时间效率(时间复杂度)——衡量算法运行速度
1.2.空间效率(空间复杂度)——衡量算法所需额外空间(如今不再特别关注)
2.时间复杂度
2.1.概念
2.2.大O的渐进表示法
2.2.1.O(F(n))
2.2.2.大O符号
2.2.3.推导大O阶方法
2.3.分类
2.3.1.最坏情况
2.3.2.平均情况
2.3.3.最好情况
2.4.常见计算
2.4.1.O(n)
2.4.2.O(m+n)
2.4.3.O(1)
2.4.4.O(n^2)
2.4.5.O(logN)
2.4.6.计算阶乘递归——O(n)
2.4.7.斐波那契递归——O(2^n)
2.4.8.O(根号n)
2.5.总结
3.空间复杂度
3.1.概念
3.2.大O渐进表示法
3.3.一般分两种
3.4.常见计算
3.4.1.冒泡排序——O(1)
3.4.2.斐波那契(迭代)——O(n)
3.4.3.求阶乘(递归)——O(n)
1.算法效率
1.1.时间效率(时间复杂度)——衡量算法运行速度
1.2.空间效率(空间复杂度)——衡量算法所需额外空间(如今不再特别关注)
2.时间复杂度
2.1.概念
算法中的基本操作的执行次数为算法的时间复杂度。(是一函数,主要看循环)
2.2.大O的渐进表示法
2.2.1.O(F(n))
如果n表示数据规模,那么O(F(n))表示算法所执行的指令数,与F(n)成正比。
2.2.2.大O符号
是用于描述函数渐进行为的数学符号。
2.2.3.推导大O阶方法
1).用常数1取代运行时间中的所有加法常数。
2).在修改后的运行次数函数中,只保留最高阶项。
3).如果最高阶项存在且不是1,则去除与这个项相乘的常数。
得到的结果就是大O阶。
例:F(n)=2n^2+2n+10 -> O(n^2)
2.3.分类
2.3.1.最坏情况
任意输入规模的最大运行次数(上界)(实际上一般都关注最坏情况,其包含了最高阶)
2.3.2.平均情况
任意输入规模的期望运行次数((最好+最坏)/ 2 )
2.3.3.最好情况
任意输入规模的最小运行次数(下界)
2.4.常见计算
2.4.1.O(n)
2n
10
->(2n+10) -> O(n)
2.4.2.O(m+n)
m
n
->m+n -> O(m+n)
2.4.3.O(1)
100 -> O(1)
2.4.4.O(n^2)
n
n
->O(n^2)
2.4.5.O(logN)
若给定算法的数据规模为n,循环不断进行除法操作(与除以几无关),终止条件直到除数==1或==0,其时间复杂度为O(logN)。其逆过程也同理:*几。如:int i = 1; i < n; i = i + i.
注:
1).logN在算法分析中表示底数为2,对数为N。有些地方也写作lgN.
2).log以a为底的n=log以a为底的b(常数) * log以b为底的n
-> log以a为底的n = log以b为底的n
->与底数无关 -> O(logN)
2.4.6.计算阶乘递归——O(n)
long factorial(int n){
return n < 2 ? n : factorial(n - 1) * n;
}2.4.7.斐波那契递归——O(2^n)
int fibonacci(int n){
return n < 2 ? n : fibonacci(n - 1) + fibonacci(n - 2);
}
2.4.8.O(根号n)
//求一个数是否是素数
private static boolean isPrime(int num){
for(int x = 2; x * x <= num; x++){
if(num % x == 0){
return false;
}
return true;
}
}2.5.总结

3.空间复杂度
3.1.概念
是对一个算法在运行过程中临时占用存储空间大小的量度。
即一个算法需要的内存大小,当前算法解决问题开辟的辅助空间大小。
3.2.大O渐进表示法
3.3.一般分两种
O(1)——没开辟额外空间
O(n)——开辟了额外数组空间
很少见O(n^2),O(logn)不存在。
3.4.常见计算
3.4.1.冒泡排序——O(1)
3.4.2.斐波那契(迭代)——O(n)
int[] fibonacci(int n){
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for(int i = 2; i <= n; i++){
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}3.4.3.求阶乘(递归)——O(n)
递归的运行需要额外开辟空间,每进行一次递归,操作系统就在系统栈上开辟一次栈帧空间。
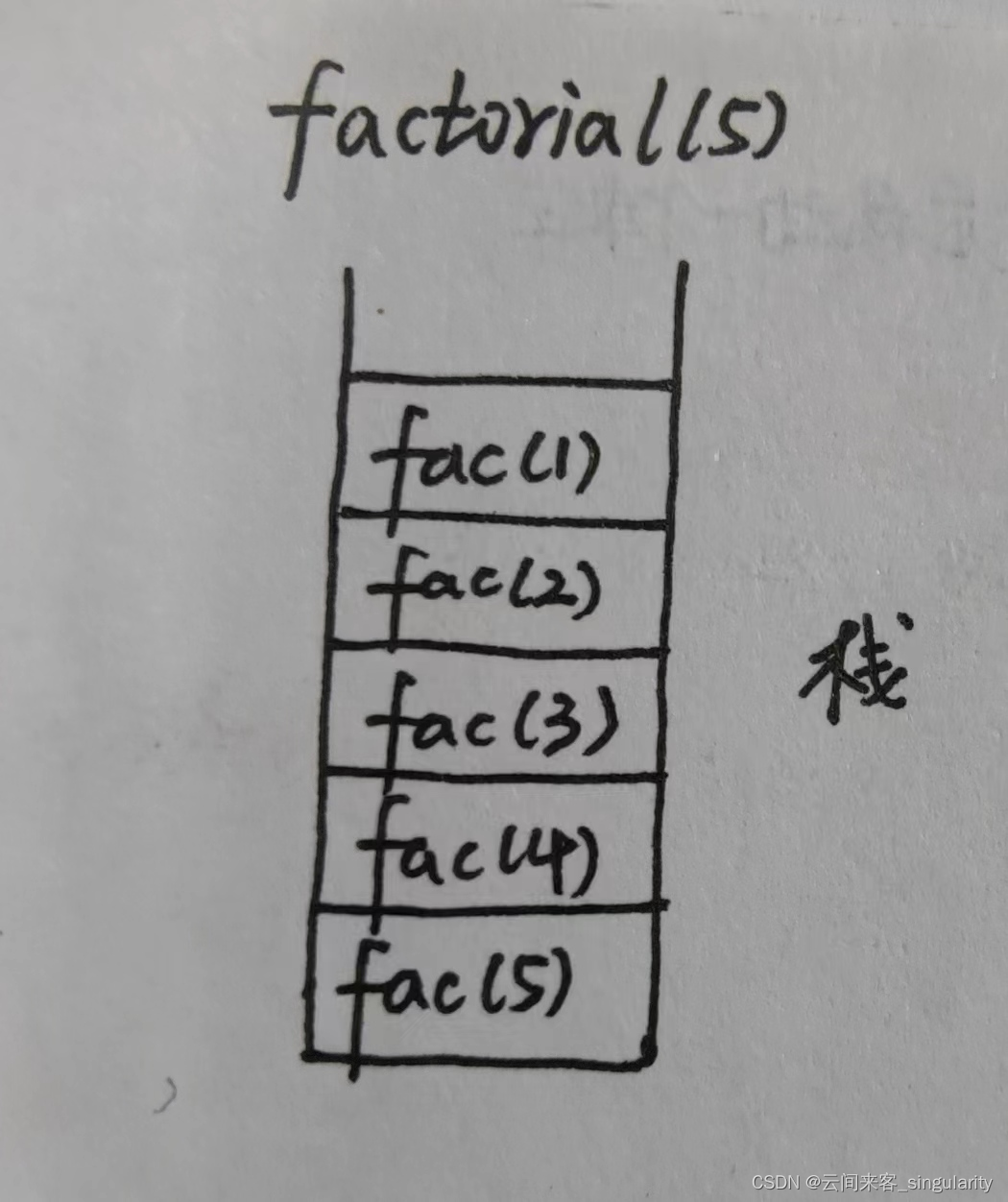
递归函数的空间复杂度取决于递归的深度(调用的次数),基本都是O(n)。
但斐波那契数列除外,递归法的时间/空间复杂度都是O(2^n),迭代法的空间复杂度是O(n)。





![[Java]注解](https://img-blog.csdnimg.cn/8b3b4ad36d1848f08f87dd9db8918be4.png)