目录

语法

说明

示例

连续时间系统的零点、极点和增益

---

        tf2zp函数的功能是将传递函数滤波器参数转换为零极点增益形式。

语法

[z,p,k] = tf2zp(b,a)

说明

        [z, p, k] = tf2zp(b, a) 从传递函数参数 b 和 a 中找到零点矩阵 z，极点向量 p，以及相关的增益向量 k。该函数将多项式传递函数表示转换为零极点增益形式。

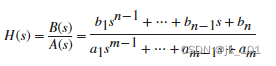
        将单输入/多输出（SIMO）连续时间系统的传递函数转换为分解的传递函数形式。

注意

        在处理正幂（例如连续时间传递函数中的s2 + s + 1）时，使用tf2zp。而在处理以逆幂表示的传递函数（1 + z^(-1) + z^(-2)）时，更适合使用类似的函数tf2zpk。

示例

连续时间系统的零点、极点和增益

        生成一个具有以下传递函数的系统。

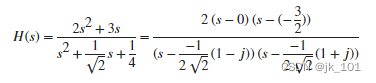
        找到系统的零点、极点和增益。使用 eqtflength 来确保分子和分母具有相同的长度。

b = [2 3];
a = [1 1/sqrt(2) 1/4];

[b,a] = eqtflength(b,a);
[z,p,k] = tf2zp(b,a)
z = 2×1

         0
   -1.5000

p = 2×1 complex

  -0.3536 + 0.3536i
  -0.3536 - 0.3536i

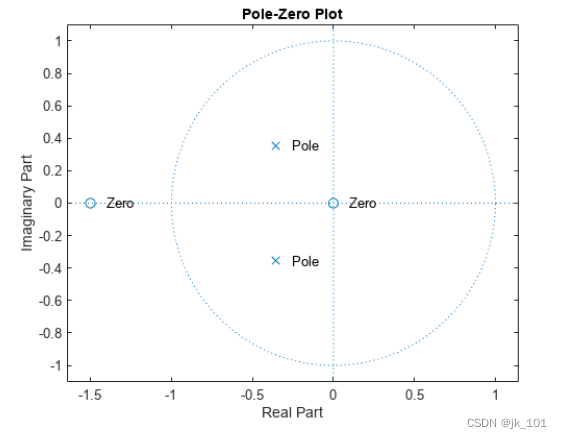
k = 2

绘制极点和零点图，以验证它们是否位于预期的位置。

zplane(b,a)
text(real(z)+0.1,imag(z),"Zero")
text(real(p)+0.1,imag(p),"Pole")

如图所示：

参数说明

b - 传递函数分子的系数

        传递函数的分子系数，指定为向量或矩阵。如果 b 是矩阵，那么 b 的每一行对应系统的一个输出。b 包含按 s 的降幂排列的系数。b 的列数必须小于或等于 a 的长度。

a- 传递函数分母的系数，通常表示为一个向量

        传递函数分母的系数，指定为一个向量。a 包含按 s 的降幂排列的系数。

z-零点

        系统的零点，返回为一个矩阵。z 的各列包含了分子中的零点，列数与系统的输出数量相同。

p-极点

        系统的极点，返回为列向量。p 包含传递函数分母系数的极点位置。

k-增益

        系统的增益，返回为列向量。k 包含每个分子传递函数的增益。