from gurobipy import *
import copy
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']

'''定义了一个线性松弛问题，并用Gurobi求解'''
initial_LP = Model('initial LP') # 定义变量initial_LP，调用Gurobi的Model，选择Initial Programming（整数规划）模型
x = {} # 创建一个空字典来存储决策变量

for i in range(2): # 创建两个决策变量
    # 下界lb为0，上界ub为正无穷，变量类型vtype为连续型，变量名称name为x0和x1
    x[i] = initial_LP.addVar(lb=0,ub=GRB.INFINITY, vtype=GRB.CONTINUOUS,name = 'x_'+str(i))

initial_LP.setObjective(100*x[0]+150*x[1],GRB.MAXIMIZE) # 目标函数，设置为最大化MAXIMIZE
initial_LP.addConstr(2*x[0]+x[1]<=10) # 约束条件1
initial_LP.addConstr(3*x[0]+6*x[1]<=40) # 约束条件2

# initial_LP.optimize() # 调用求解器
# for var in initial_LP.getVars():
#     print(var.Varname,'=',var.x)

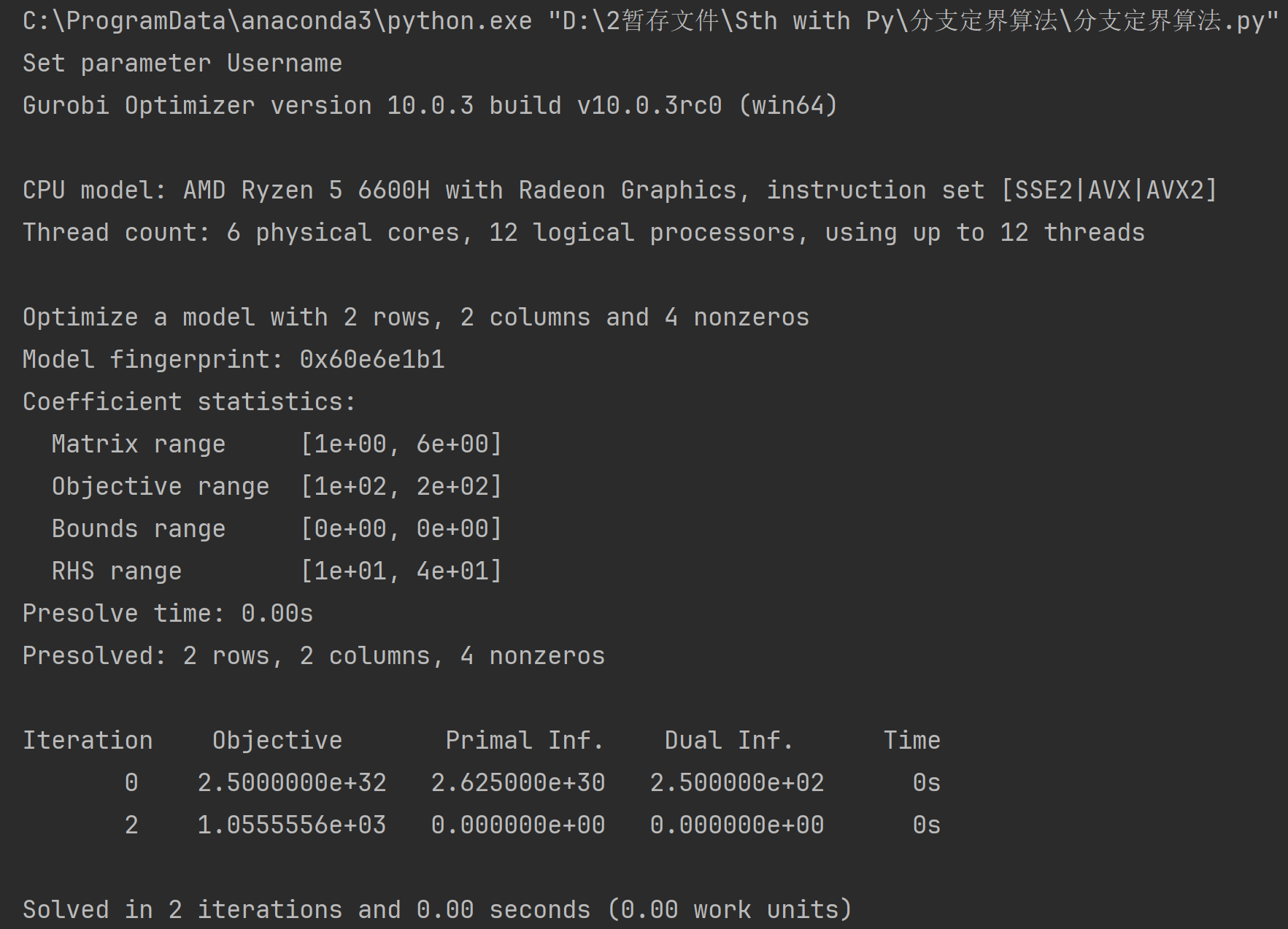
'''输出信息：
    Set parameter Username: 这是一个提示，通常在你的 Gurobi 环境中需要设置用户名
    Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64): 这是 Gurobi 优化器的版本信息，指出你使用的是版本 10.0.3
    CPU model: AMD Ryzen 5 6600H with Radeon Graphics, instruction set [SSE2|AVX|AVX2]: 这部分提供了计算机的 CPU 模型信息，以及支持的指令集
    Thread count: 6 physical cores, 12 logical processors, using up to 12 threads: 这部分提供了有关计算机处理器的信息，包括物理核心数量和逻辑处理器数量，以及正在使用的线程数
    Optimize a model with 2 rows, 2 columns and 4 nonzeros: 这部分提供了线性规划问题的规模信息。问题包含 2 个约束（rows），2 个变量（columns），以及 4 个非零元素
    Model fingerprint: 0x60e6e1b1: 这是问题的唯一标识，可以用于识别不同的问题实例
    Coefficient statistics: 这一部分提供了与问题的系数统计信息，包括矩阵范围、目标函数范围、边界范围以及右侧（约束右手边）范围
    Iteration Objective Primal Inf. Dual Inf. Time: 这一部分是 Gurobi 求解线性规划问题时的迭代信息。其中包括了每次迭代的目标值、主问题不可行度、对偶问题不可行度和用时
    Primal Inf（主问题不可行度）:当 Primal Inf 的值为零时，表示找到了一个可行的解决方案，即问题的所有约束条件都得到满足。如果 Primal Inf 的值大于零，这意味着问题不是可行的，即无法找到满足所有约束条件的解决方案。Primal Inf 的绝对值越大，表示问题的不可行度越高
    Dual Inf（对偶问题不可行度）:当 Dual Inf 的值为零时，表示对偶问题的解是可行的，这通常是好的。如果 Dual Inf 的值大于零，这意味着对偶问题是不可行的，这可能会影响原始问题的最优解'''

'''定义一个名叫Node的类，用于表示分支定界算法中的节点'''
class Node:
    '''初始化对象的属性'''
    def __init__(self):
        self.model = None
        self.x_sol = {} # 用于存储子问题的最优解
        self.x_int_sol = {} # 用于存储子问题的最优整数解
        self.local_LB = 0  # 用于存储子问题的最优下界
        self.local_UB = np.inf # 用于存储子问题的最优上界
        self.is_integer = False # 指示节点的最优解是否为整数
        self.branch_var_list = []  # 用于存储需要进行分支的变量列表

    '''定义深拷贝原始节点的函数'''
    def deepcopy(node): # node就算要深拷贝的节点
        new_node = Node() # 首先创建了一个新的'Node'对象
        new_node.local_LB = 0
        new_node.local_UB = np.inf
        # 确保了新节点的下面两个属性是独立的
        new_node.x_sol = copy.deepcopy(node.x_sol) # 用于存储子问题的最优整数解
        new_node.x_int_sol = copy.deepcopy(node.x_int_sol) # 指示节点的最优解是否为整数
        new_node.branch_var_list = [] # 用于存储需要进行分支的变量列表
        new_node.model = node.model.copy()  # 将原始节点的模型进行深拷贝，以创建新节点的模型
        new_node.is_integer = node.is_integer # 表示新节点的整数性属性与原始节点相同
        return new_node

'''分支定界算法函数'''
def branch_and_bound(initial_LP):
    '''初始化上下界列表'''
    trend_UB = []
    trend_LB =[]
    initial_LP.optimize() # 调用求解器进行求解
    global_LB = 0
    global_UB = initial_LP.ObjVal # 将最优上界存储在global_UB中
    eps = 1e-3 # 阈值，可用来判断是否为整数解。比如2.38取整之后为2，与2.38相差超过eps，则认为不是整数解
    incumbent_node = None # 存储当前最优解的节点
    Gap = np.inf # 当前最优解和全局上界的差距

    '''分支定界的开始'''
    Queue = [] # 用队列实现深度优先搜索

    node = Node() # 创建根节点
    node.local_LB = 0 # 局部下界初始化为0

    node.local_UB = global_UB # 根节点的局部上界初始化为全局上界

    node.model = initial_LP.copy() # 由于是子问题，因此需要拷贝出一个独立的问题
    node.model.setParam('OutputFlag',0) # 子问题求解过程不需要输出详细信息
    Queue.append(node) # 将根节点输入队列

    '''分支定界算法的主循环'''
    cnt = 0 # 计数器
    while(len(Queue)>0 and global_UB - global_LB >eps) : # 当队列为空或者全局上下界之差小于阈值时退出循环
        cnt += 1 # 记录迭代次数
        # 使用深度优先搜索，后进先出
        # pop: 从列表中删除最后一个元素，并返回该元素的值
        current_node = Queue.pop() # 当前节点的线性模型
        current_node.model.optimize()
        Solution_status = current_node.model.status # 获取求解状态

        # 跟踪当前解的性质
        Is_Integer = True # 初始化为整数
        Is_pruned = False # 初始化为不剪枝

        '''若子问题的求解有效'''
        if(Solution_status == 2): # 当求解状态为2时，当前模型成功收敛到最优解
            '''检查解是否为整数'''
            for var in current_node.model.getVars(): # 循环遍历当前节点的所有变量
                current_node.x_sol[var.VarName] = var.x # 提取决策变量
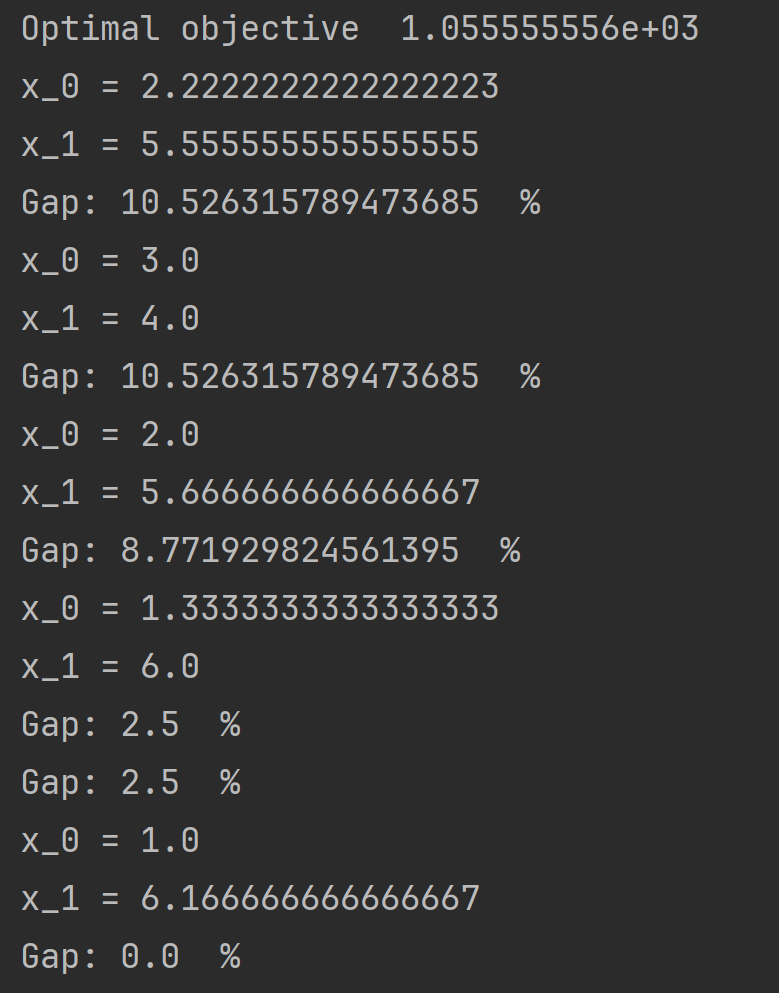
                print(var.VarName,'=',var.x) # 例如输出 x_0 = 2.2222222222222223
                # 把当前解化为整数解
                current_node.x_int_sol[var.VarName] = (int)(var.x) # 取整后储存起来

                if (abs( (int)(var.x)-var.x)>= eps): # 如果取整后和原始解相差超过eps
                    Is_Integer = False # 则认为不是整数解
                    current_node.branch_var_list.append(var.VarName) # 添加到需要分支的列表中

            '''更新局部上界和局部下界'''
            if(Is_Integer == True): # 如果当前解是整数解
                '''当当前节点包含一个整数解时，这是一个非常好的情况，因为找到了一个可行的整数解，它是问题的一个潜在最优解'''
                current_node.local_LB = current_node.model.ObjVal # 将当前节点的局部下界更新为当前节点模型的目标函数值
                current_node.local_UB = current_node.model.ObjVal # 将当前节点的局部下界更新为当前节点模型的目标函数值
                current_node.is_integer = True # 表示当前节点包含整数解
                if(current_node.local_LB > global_LB): # 如果当前节点的局部下界大于全局下界
                    global_LB = current_node.local_LB # 更新全局下界的值
                    incumbent_node = Node.deepcopy(current_node) # 深拷贝以保存当前节点

            else: # 如果不是整数解
                '''当当前节点的解不是整数解时，不能将解视为潜在的整数最优解，因为目标是寻找整数解'''
                Is_Integer = False
                current_node.local_UB = current_node.model.ObjVal # 将当前节点的局部上界更新为当前节点模型的目标函数值
                if current_node.local_UB < global_LB: # 如果局部上界小于全局下界
                    Is_pruned = True # 则剪枝
                    current_node.is_integer = False # 设置为非整数解
                else:
                    Is_pruned = False # 不剪枝
                    current_node.is_integer = False
                    for var_name in current_node.x_int_sol.keys(): # 遍历每个整数解
                        var = current_node.model.getVarByName(var_name) # 获取当前节点的变量名
                        current_node.local_LB += current_node.x_int_sol[var_name]*var.Obj # 一种启发式算法去更新局部下界
                        # 对父节点的解执行向下取整操作，然后计算该整数解对于局部下界的目标函数值贡献
                        # 通过向下取整解得到的解可能仍然是问题的可行解

                    '''更新全局下界'''
                    if (current_node.local_LB > global_LB): # 如果局部下界大于全局下界，那么该节点可以继续分支
                        global_LB = current_node.local_LB
                        incumbent_node = Node.deepcopy(current_node)

                    '''分支'''
                    branch_var_name = current_node.branch_var_list[0] # 获取需要分支节点名称的第一个
                    # 分支的两个节点边界
                    left_var_bound = (int)(current_node.x_sol[branch_var_name])
                    right_var_bound = (int)(current_node.x_sol[branch_var_name])+1

                    '''创建左右节点'''
                    left_node = Node.deepcopy(current_node)
                    right_node = Node.deepcopy(current_node)

                    '''给左节点添加约束'''
                    temp_var = left_node.model.getVarByName(branch_var_name) # 获取要分支的对象
                    left_node.model.addConstr(temp_var <= left_var_bound,name = 'branch_left_'+str(cnt)) # 小于等于的约束
                    left_node.model.update() # 添加条件后更新模型

                    temp_var = right_node.model.getVarByName(branch_var_name)
                    right_node.model.addConstr(temp_var >= right_var_bound,name = 'branch_right_'+str(cnt)) # 大于等于的约束
                    left_node.model.update()

                    '''节点入队'''
                    Queue.append(left_node)
                    Queue.append(right_node)

        elif(Solution_status !=2) : # 如果线性模型求解不成功
            Is_Integer = False
            Is_pruned = True

        '''更新上界'''
        temp_global_UB = 0
        for node in Queue: # 遍历队列的每个节点并进行求解
            node.model.optimize()
            if(node.model.status == 2):
                if(node.model.ObjVal >=temp_global_UB):
                    temp_global_UB = node.model.ObjVal # 更新全局上界
        global_UB = temp_global_UB
        Gap = 100*(global_UB - global_LB)/global_LB
        print('Gap:',Gap,' %')
        trend_UB.append(global_UB)
        trend_LB.append(global_LB) # 下界在前面已经更新了

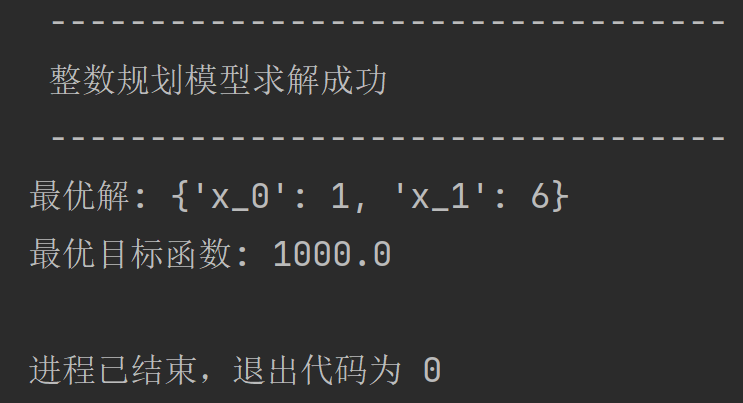
    print(' ---------------------------------- ')
    print(' 整数规划模型求解成功 ')
    print(' ---------------------------------- ')
    print('最优解:', incumbent_node.x_int_sol)
    print('最优目标函数:', global_LB)
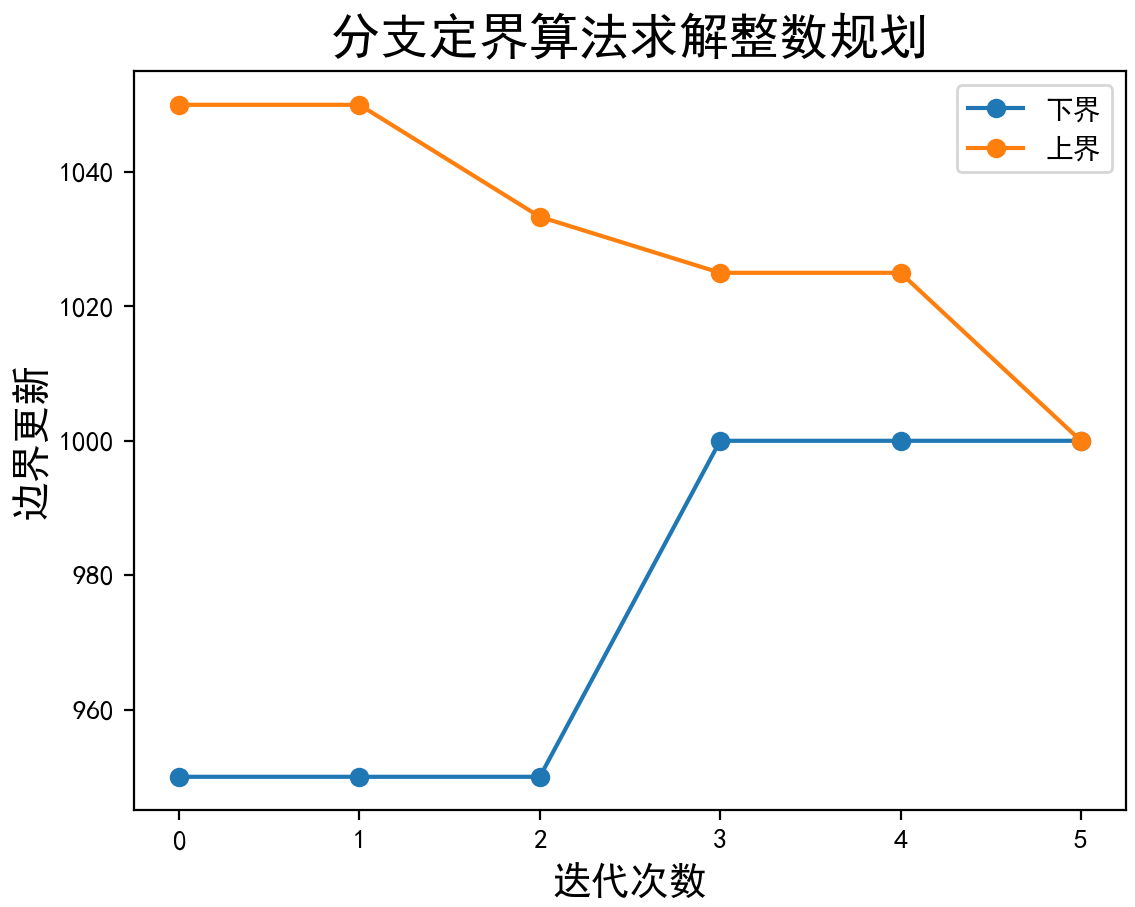
    plt.figure()
    plt.plot( trend_LB , label="下界",marker='o')
    plt.plot( trend_UB, label="上界",marker='o')
    plt.xlabel('迭代次数',fontsize=14)
    plt.ylabel('边界更新',fontsize=14)
    plt.title("分支定界算法求解整数规划",fontsize=18)
    plt.legend()
    plt.show()
    return incumbent_node, Gap

'''调用分支定界算法'''
result, gap = branch_and_bound(initial_LP)