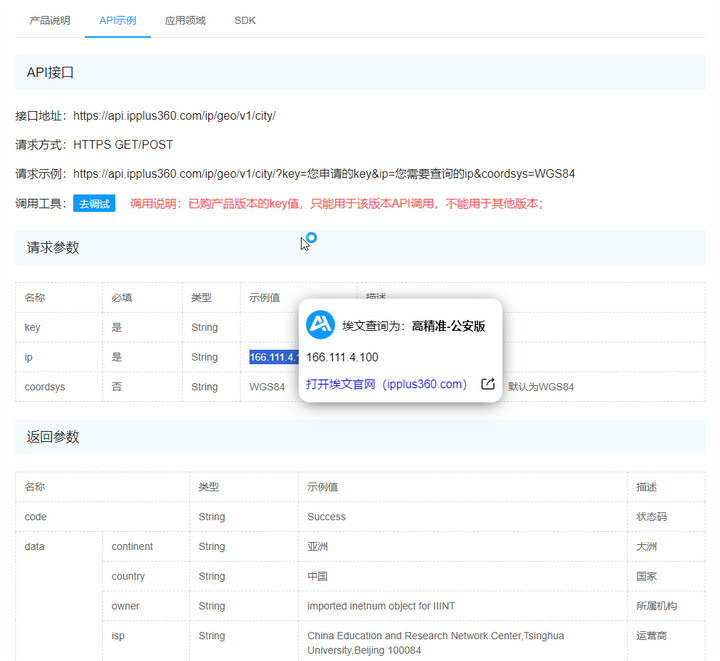
0. 简介

Camera与LiDAR之间的外部标定研究正朝着更精确、更自动、更通用的方向发展，由于很多方法在标定中采用了深度学习，因此大大减少了对场景的限制。然而，数据驱动方法具有传输能力低的缺点。除非进行额外的训练，否则它无法适应数据集的变化。随着基础模型的出现，这个问题可以得到显著缓解，通过使用分割任意模型（Segment Anything Model，SAM），我们这次提出了一种新的激光雷达相机标定方法，该方法不需要额外的训练，并适用于常见场景。相关的代码可以在Github上获得。

1. 主要贡献

首先使用SAM对整个图像进行语义分割，得到一组掩码，在没有在点云和掩模之间建立明确的对应关系，而是计算掩模内点云属性的一致性，包括其强度、法向量和分割类。如图1所示，在正确的外在条件下，汽车mask内点的强度具有更高的一致性。对于法线向量，plane masks上的点应具有一致的法线方向，简单地通过平面拟合和欧氏聚类得到点云的分割类。vehicles和trunks 等目标将聚集在一个类别中，因此mask上也具有一致性！论文计算了具有这三个属性的每个mask的一致性得分，通过给出一个初始的外在值，可以通过最大化所有mask的总分来优化它。

图1. 通过正确的外参(a)和错误的外参(b)投影到车的掩模上的点云。点的颜色表示强度值。

为此，本文主要工作的贡献如下：

1）我们提出了一种新颖的自动LiDAR-相机外参校准方法，使用SAM和点云一致性，不需要额外的训练。

2）外参参数的优化标准是点云在掩模上的强度、法线向量和分割类别的一致性，使我们的方法适用于大多数场景。

3）我们在多个数据集上验证了我们的方法，证明了其通用性和可比性精度。

2. 方法概述

整个过程可以分为三个部分。对于图像分割，我们使用SAM生成整个图像的掩模。对于点云，我们实现了法线估计、简单的分割方法和强度归一化，以生成每个点的对应属性。然后，优化目标是使落在一个掩模上的点具有接近的属性值。我们设计了一个评估一致性的得分函数。进行几轮搜索以获得最终结果。图2显示了我们提出的方法的流程。

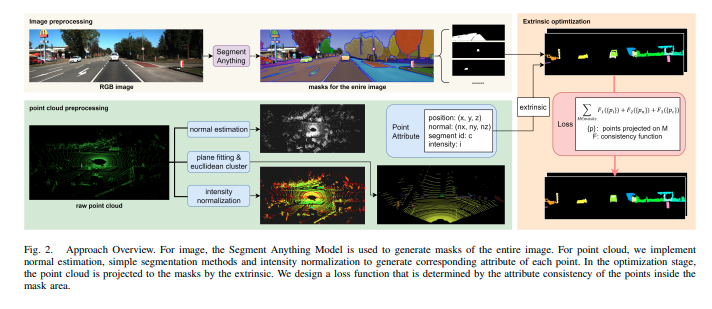
图2. 方法概述。对于图像，使用Segment Anything模型生成整个图像的掩码。对于点云，我们实现了法线估计、简单的分割方法和强度归一化，以生成每个点的相应属性。在优化阶段，通过外参将点云投影到掩码上。我们设计了一个损失函数，该函数由掩码区域内点的属性一致性决定。

3. 数据预处理

3.1 图像分割

首先在整个图像上应用SAM，以获取许多不同对象的掩模。由于我们使用点云的一致性，我们希望分割更加细致和详细。因此，我们调整SAM的超参数以获得更多的掩模，并减少重叠区域。这些掩模被注释为 M = { M i ∣ i = 0 , 1 , … , N } \mathbb{M} = \{M_i | i = 0, 1, …, N\} M={Mi​∣i=0,1,…,N}。每个掩模是一个与图像相同大小的二进制矩阵。值 M i ( u , v ) = { 0 , 1 } M_i(u, v) = \{0, 1\} Mi​(u,v)={0,1}表示像素$(u,v)$是否属于第$i$个分割。

3.2 点云预处理

预处理有三个部分：法线估计、强度归一化和分割。

对于法线估计，有许多方法[32]，[33]可以直接使用。在这里，我们选择了一个简单的方法，足以满足我们的应用需求。表面上的一个点的法线方向被近似为与表面相切的平面的法线。平面法线可以通过分析由查询点的一些最近邻创建的协方差矩阵的特征向量和特征值或主成分分析（PCA）来估计。使用K-d树数据结构进行高效的k最近邻（KNN）搜索。

点云的强度通过比例因子进行归一化，以便在点云的强度根据LiDAR类型不同而不同的情况下进行后续的一致性计算。

除了这两个属性之外，我们对点云进行简单的分割方法。我们首先通过RANSAC算法进行平面拟合，提取场景中的大型平面，如地面和墙壁。然后我们对剩余的点云应用一些欧几里得聚类[32]，并获得个体对象的聚类，如车辆和树木。我们为点分配一个数字$c$，表示它属于哪个类别。 点云中点的最终属性可以表示为：

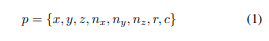
这是点$P$的位置、法线向量、反射率和分割类别。

3.3 外参优化 （重点内容）

1）一致性函数： 点$p$可以通过初始外参$T$投影到图像帧中：

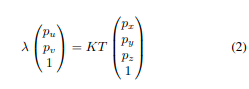
在这里，我们假设内参$K$已知。然后对于每个掩模$M_i$，我们可以得到一组落在其上的点：

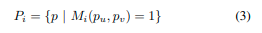
可以通过以下公式计算点集$P_i$的一致性得分：

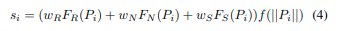
其中，$F_R(\cdot )、F_N(\cdot )、F_S(\cdot )$是反射率、法线向量和分割类别的对应函数，$w_R$、$w_N$、$w_S$是它们的权重。在实践中，我们使用$w_R=w_N=w_S$。$f(\cdot )$是根据Pi中点的数量进行调整的函数。 反射率一致性可以通过所有值的标准差(std)简单计算：

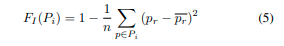
假设大小为(3 × n)的矩阵$A$由$P_i$中的法线向量组成。法线向量的一致性函数$F_N$表示为：

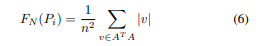
它是所有**向量成对点积的平均值。对于分割类别，首先对每个类别的点进行计数并按从大到小的顺序排序。**这表示为$(c_0，c_1，\dots )$，其中$c_i$是第$i$个最大类别中的点数。一致性是所有类别的加权和：

…详情请参照古月居