归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。

1. 基本思想

归并排序使用分治思想，分治模式下每一层递归有三个步骤：

• 分解（divide)：将n个元素分成两个含n/2个元素的子序列
• 解决（conquer)：用合并排序法对两个子序列递归的排序
• 合并（combine）：直接合并两个已排序好的子序列

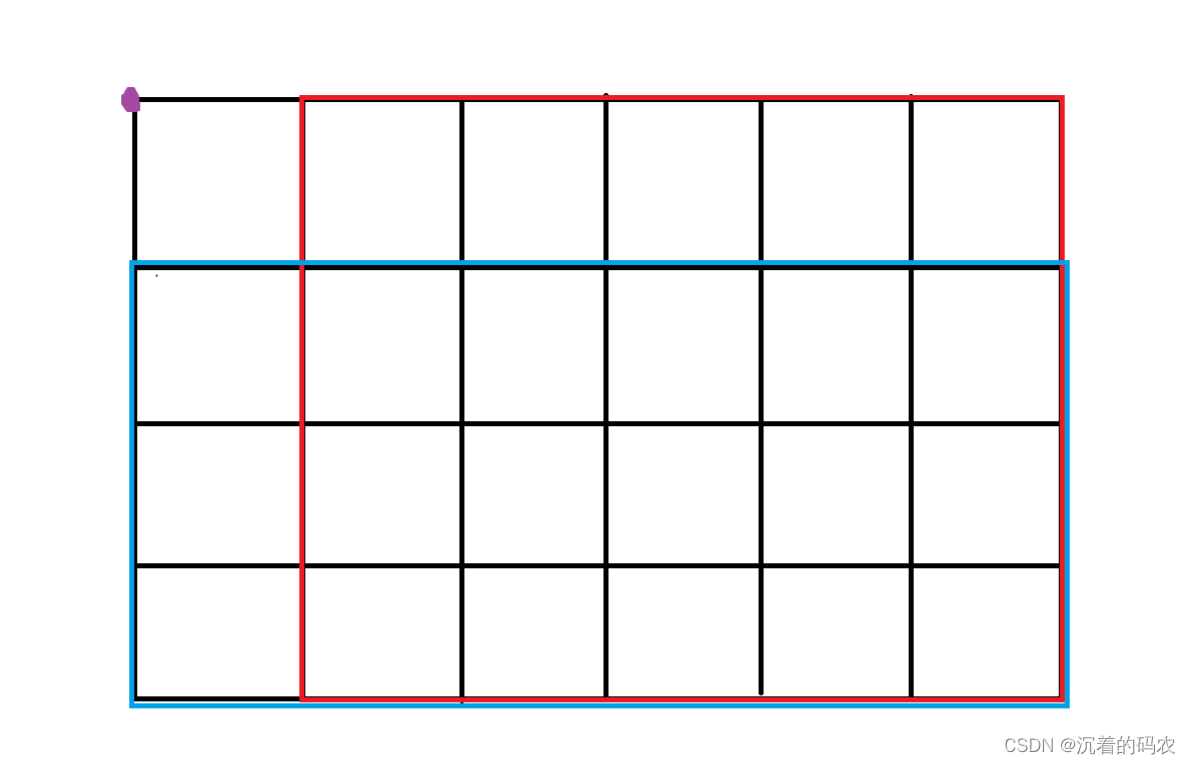
解释：上图中首先把一个未排序的序列从中间分割成2部分，再把2部分分成4部分，依次分割下去，直到分割成一个一个的数据，再把这些数据两两归并到一起，使之有序，不停的归并，最后成为一个排好序的序列。

2. 时间复杂度

归并排序中最主要的操作就是将两个有序序列合并，该操作的算法复杂度对归并排序的算法复杂度影响最大。

算得，时间复杂度为$O(nlo{g}_{2}n)$！

3. 算法实现

它的思路是先将数组分成两个子数组，然后分别对两个子数组进行归并排序，最后将两个有序的子数组合并成一个有序的数组。在合并的过程中，使用一个临时数组reg来存储合并后的结果，最后再将结果复制回原数组arr中。

#define N 100
int arr[N],reg[N];
void merge_sort(int l,int r){
    if(l>=r) return;
    int mid=(l+r)/2;
    int i=l,j=mid+1; //两个指针，分别指向分治后的两个子数列
    int k=l; //用于更新临时数组reg内的值
    //分治
    merge_sort(l,mid);
    merge_sort(mid+1,r);
    //合并
    while(i<=mid && j<=r){
        if(arr[i]<=arr[j]) reg[k++]=arr[i++];
        else reg[k++]=arr[j++] ;
    }
    while(i<=mid) reg[k++]=arr[i++];
    while(j<=r) reg[k++]=arr[j++];
    for(int k=l;k<=r;k++)
        arr[k]=reg[k];

}