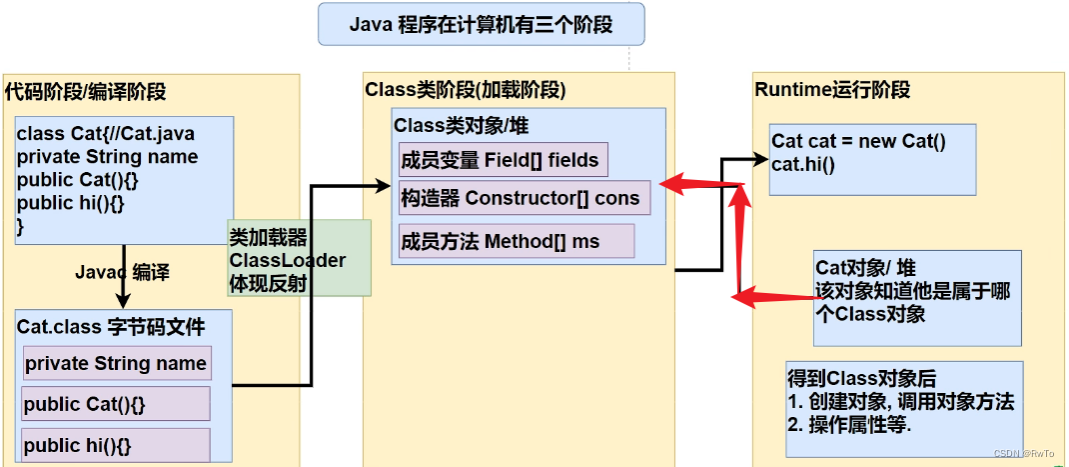
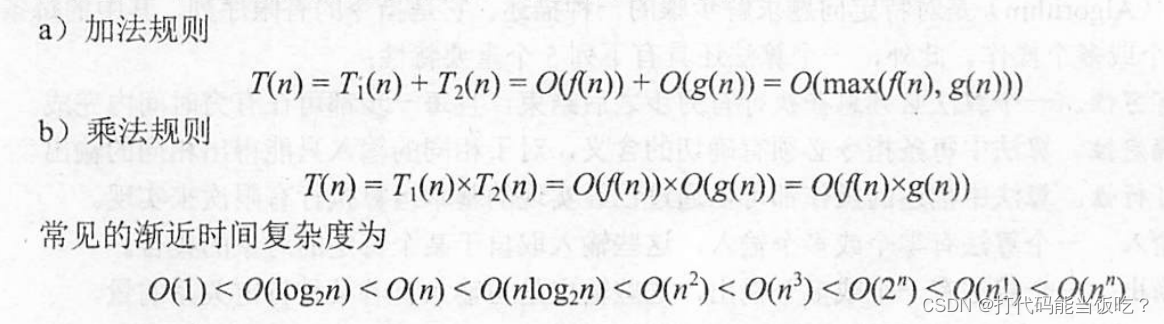图论与网络优化

2.概念与计算

2.1 图的定义

2.1.1 定义

图(graph) $G$ 是一个有序的三元组，记作 $G=<V(G),E(G),\psi (G)>$ 。
$V (G)$ 是顶点集。 $E (G)$ 是边集。 $\psi (G)$ 是关联函数，；例如 $\psi_G (e)=v_iv_j$ 。
$N_G(v)$ 表示点 $v$ 的一阶邻域点。

相邻：与同一个顶点关联的两条边是相邻的。
环：两个端点重合的边称为环。
连杆：端点不重合的边成为连杆。
$k$ 重边：连接同一对顶点的 $k$ 条边。
单边：一对顶点之间只有一条边。
简单图：无环无重边

2.1.2 度

度：与顶点 $v$ 关联的边的数目，记作 $d (v)$ 。
度序列： $d(v_1),d(v_2),...,d(v_v))$
孤立点：度为 $0$ 。
悬挂点：度为 $1$ 。
悬挂边：与悬挂点相关联的边。
偶点：度为偶数的顶点。
奇点：度为奇数的顶点。
最小度 $\delta(G)$ ：图 $G$ 顶点度的最小值。
最大度 $\Delta(G)$ ：图 $G$ 顶点度的最大值。

握手引理： $\sum_{v\in V} = 2 \epsilon$ 。
例题：空间中不存在有奇数个面并且每个面只有奇数个棱的多面体。
思路：将面抽象为点，两面之间的棱为边，则转化成了有奇数个点且每个点都是奇数度的图，与握手引理矛盾，得证。

例题：证明非负整数序列 $d_1,d_2,...,d_v)$ 是某个图的度序列当且仅当 $\sum_{i=1}^{v} d_i$ 是偶数。
思路：先画出 $v$ 个孤立点，然后选序列中度大于 $1$ 的点连环直至将每个点仍需添加的度为 $0$ 或 $1$ 。然后将两两选择度为 $1$ 的点。能连通即可得证。

图序列：简单图的度序列。
判断是否为图序列：非负整数序列 $(d_1,d_2,...,d_v)(d_1 \geq d_2 \geq ... \geq d_v)$ 是图序列当且仅当 $\sum_{i=1}^v d_i$ 是偶数，并且对一切整数 $k(1\leq k\leq v-1$ ，有 $\sum_{i=1}^{k} \leq k(k-1) \leq \sum_{i=k+1}^{v}min \{k,d_i\}$ .
例题：(1,2,2,4,5);(1,2,3,3,4,5);(1,2,3,4,4,5) 三个是否是图序列？
思路：第一个不是图序列，当点数为 $5$ 时，不存在度为 $5$ 的简单图。第二个是图序列。第三个不是图序列，先画出度为 $5$ 的点的连边，然后只有三个点还能连边，需要的度依次为 $2, 3, 3$ ，简单图中的三个点不可能连出度为 $3$ 的连边情况。

2.1.3 同构

同构：若两个图顶点之间建立一一对应的关系，且任意一对顶点的边数对应相同，则称两图是同构的。

2.2 子图和连通分支

2.2.1 子图

子图：设 $H$ 和 $G$ 为两个图。若 $\subseteq V(G)$ 且 $\subseteq E(G)$ ，则 $H$ 为 $G$ 的子图。记作 $\subseteq G$ 。
相等：设 $H$ 和 $G$ 为两个图。若 $V (H) = V (G)$ 且 $E (H) = E (G)$ ，则 $H$ 为 $G$ 相等。记作 $H = G$ 。
真子图：若 $\subseteq G$ 且 $\neq G$ ，则称 $H$ 是 $G$ 的真子图，记作 $\subset G$ 。
支撑(生成)子图：若 $V (H) = V (G)$ 且 $\subseteq E(G)$ ，则称 $H$ 是 $G$ 的支撑子图或生成子图。
基础简单图：对图 $G$ 去除重边和环后的图 $H$ 。

2.2.2 导出子图

导出子图：设 $V^{'}$ 是 $V (G)$ 的非空子集，以 $V^{'}$ 为顶点集，以 $\in E(G) | u,v \in V'}$ 为边集的 $G$ 的子图称为 G 的由 $V^{'}$ 导出的子图，记作 $G [V^{'}]$ ，简称为 $G$ 的导出子图。

2.2.3 连通分支

途径的起点/终点/长度/逆转/衔接/节： $W=v_oe_1v_1e_2...e_kv_k$ ，这里 $v_i\in V(0\leq i \leq k),e_j=v_{j-1}v_j \in E(1 \leq j \leq k)$ ， $v_0$ 称为 $W$ 的起点， $v_k$ 称为 $W$ 的终点，之间的 $v$ 称为 $W$ 的内部点。 $W$ 称为 $G$ 的 $v_0,v_k)$ 途径。 $k$ 为 $W$ 的长度。逆转如字面意思。衔接意味对于两个不同的 $W$ ，其中一条 $W$ 的终点为另一个 $W$ 的起点，则两条 $W$ 可以衔接。节是 $W$ 序列中的子集。

迹：途径 $w$ 的边互不相同，则称 $W$ 为迹。若起点终点相同，则 $W$ 为闭迹。
链：途径 $w$ 的顶点互不相同，则称 $W$ 为链。一个顶点也称为一条链。
圈：起点、内部点互不相同的闭迹称为圈，长为 $k$ 的圈称为 $k$ 圈。根据 $k$ 的奇偶性，相应地称 $k$ 圈为奇圈和偶圈。
连通：若图 $G$ 中存在 $(u, v)$ 链，则顶点 $u$ 和 $v$ 在图 $G$ 中是连通的。
连通分支(数)： $V$ 的非空划分 $(V_1,V_2...,V_\omega)$ ，导出子图 $G[V_1],G[V_2],...,G[V_\omega]$ 称为 $G$ 的连通分支。 $\omega(G)$ 为图 $G$ 的连通分支数。

2.2.4 距离

距离：图 $G$ 中所有 $(u, v)$ 链的最短链，记为 $d (u, v)$ ，被称之为 $u, v$ 之间的距离。
例题：设 $G$ 是连通图，且 $G$ 中至少有一对顶点不相邻，证明存在 $\in V$ ，使 $\in E$ ，但 $\notin E$ 。
思路：设 $\in V$ 且 $\notin E$ 。因 $G$ 连通，故 $G$ 中存在最短 $(x, y)$ 链 $P=xv_1v_2...y$ 。
由 $P$ 的最短性可知 $xv_2 \notin E$ ，于是令 $u=x,v=v_1,w=v_2$ ，则有 $\in E,vw \in E$ 但 $\notin E$ 。

2.3 重要图类

2.3.1 完全图

完全图：含有 $C_{n}^{2}$ 条边，且每对顶点都相邻的简单图，记作 $K_n$ 。
空图：边集为空的图。
平凡图：图中只有一个顶点。
非平凡图：除了平凡图以外的图。
例题：在任意 $6$ 个人聚会上，要么有 $3$ 个人相互认识，要么有 $3$ 个人相互不认识。
思路：先构造 $6$ 阶完全图 $K_6$ ，其中 $V = {v_1,v_2,...,v_6}$ 。 $v_i$ 代表第 $i$ 个人。
若 $v_i$ 与 $v_j$ 互相认识，则染这条边为红色边，否则为蓝色边。于是问题转成了图中必定存在同色三角形问题。因此得证。

2.3.2 正则图

正则图/k正则图：每个顶点的度都相等(都为 $k$ )的图称为( $k$ )正则图。一般指的是简单图。
例题：对于任意的正整数 $n$ , $nk$ 为偶数，当 $\geq k + 1$ ， $n$ 阶 $k$ 正则图存在吗？
思路：
$\gamma_1$ 法则：构造偶数正则图法则。
设 $G$ 是 $v$ 阶 $k$ 正则图，且 $k = 2 m$ ， $\geq 1$ ，按以下步骤生成新图 $G^{'}$ ：
step 1：在图 $G$ 中任取 $m$ 条互不相邻的边： $v_1v_2,v_3v_4,...,v_{2m-1}v_{2m}$ 并删除。
step 2：增加新的顶点 $v$ ，并向所有被删边的点增加一条新边 $vv_i(i=1,2,...,2m)$ ，得到新图 $G^{'}$ 。

$\gamma_2$ 法则：构造奇数正则图法则。
设 $G$ 是 $v$ 阶 $k$ 正则图，且 $k = 2 m + 1$ ， $\geq 1$ ，按以下步骤生成新图 $G^{'}$ ：
step 1：在图 $G$ 中任取 $m$ 条互不相邻的边： $v_1v_2,v_3v_4,...,v_{2m-1}v_{2m}$ 并删除。
step 2：再在图 $G$ 中任取 $m$ 条互不相邻的边： $u_1u_2,u_3u_4,...,u_{2m-1}u_{2m}$ 并删除。
(step 1 和 step 2 中可能会出现重复点)
step 3：增加新的顶点 $w_1$ ，并向 step 1 中所有被删边的点增加一条新边 $w_1v_i(i=1,2,...,2m)$ 。
step 4：再增加新的顶点 $w_2$ ，并向 step 2 中所有被删边的点增加一条新边 $w_2u_i(i=1,2,...,2m)$ 。
step 5：加边 $w_1w_2$ ，得新图 $G^{'}$ 。

定理： $n$ 阶 $k$ 正则简单图存在的充要条件是 $\leq n-1$ 且 $nk$ 为偶数。
证明：设 $G$ 是 $n$ 阶 $k$ 正则简单图，每个顶点最多与其他 $n - 1$ 个顶点相邻，因此 $\leq n-1$ 成立。
设 $k = 2 m$ ，取 $G=K_{k+1}$ ，则 $G$ 为 $k$ 正则图。根据 $\gamma_1$ 法则，顶点每次可以增加 $1$ 而点的度数不变。因此可以得到 $n$ 阶 $k$ 正则图。

2.3.3 二部图

(完全)二部图：若顶点集可以划分为两个子集 $X$ 和 $Y$ ，使得 $G$ 中每条边的一端点在 $X$ 中，另一个端点在 $Y$ 中，则称 $G$ 图为二部图。二部图 $G$ 记作 $G = (X, Y, E)$ 。若集合 $X$ 中的每个点都与 $Y$ 中所有点都恰好有一条边，且 $X 、 Y$ 均不为空集，则该图记作完全二部图，记作 $K_{m,n}$ 。

定理：图 $G$ 的二部图，当且仅当 $G$ 中不含奇圈。
证明：
step 1：
设 $G = (X, Y, E)$ 是二部图， $C=(v_0v_1...v_kv_0)$ 是 $G$ 中的一个圈，长度为 $k + 1$ 。
设 $v_0 \in X$ ，于是后面节点依次属于 $Y$ 和 $X$ 。因此得到 $v_{2i} \in X，v_{2i+1} \in Y$ 。
因此 $k = 2 l + 1$ 。该圈为偶圈。
step 2：
设 $G$ 连通(若不连通则取一个连通分支证明之)。在 $G$ 中任取一个顶点 $u$ ，令 $X=\{x|d(u,x)为偶数\}$ ， $Y=\{y|d(u,y)为奇数\}$ 。显然 $X 、 Y$ 是图 $G$ 的一个划分。
为了证明 $G$ 是二部图，只需证明 $X$ 或 $Y$ 中任何两个顶点都不相邻。
设 $v, w$ 是 $X$ 中任意两个顶点，令 $P$ 是 $G$ 中最短 $(u, v)$ 链，Q 是 $G$ 中最短 $(u, w)$ 链。
设 $P$ 与 $Q$ 的最后一个公共顶点是 $u_1$ 。因为 $P$ 和 $Q$ 都是最短链，因此 $P$ 的 $u,u_1)$ 节和 $Q$ 的 $u,u_1)$ 节都是最短 $u,u_1)$ 链，从而长度相等。如下图：
例题示意图
又因 $P$ 和 $Q$ 的长度都为偶数，故 $P$ 的 $u_1,v)$ 节 $P_1$ 和 $Q$ 的 $u_1,w)$ 节 $Q_1$ 有相同奇偶性，于是 $(v, w)$ 链 $P_1^{-1}Q_1$ 的长是偶数。因此若 $v$ 与 $w$ 相邻，则 $P_1^{-1}Q_1wv$ 就是 $G$ 中的一个奇圈，与假设矛盾。

2.4 有向图

2.4.1 定义

有向图：有向图 $D$ 指一个有序三元组 $(V(D),A(D),\psi_D)$ ，其中 $\neq \varnothing$ ， $\cap A(D) = \varnothing$ 。 $V (D)$ 是顶点集。 $A (D)$ 是弧集。 $\psi_D$ 称为 $D$ 的关联函数，使得 $D$ 每条弧对应于 $D$ 的有序定点对。 $\psi_D(a)=(u,v)$ 中 $u$ 是弧 $a$ 的尾， $v$ 称为 $a$ 的头。

2.4.2 基础图

基础图：在有向图中去掉弧上箭头的图。
定向图：对图 $G$ 的每条边规定方向后的图。
相邻、连通、圈、子图 的概念和含义不变。

2.4.3 出度和入度

入弧：有向图 $D$ 中以顶点 $v$ 为头的弧。
出弧：有向图 $D$ 中以顶点 $v$ 为尾的弧。
入度：记作 $d_D^-(v)$ ，称为 $v$ 的入度。
出度：记作 $d_D^+(v)$ ，称为 $v$ 的出度。
对于任何有向图D，有： $\sum_{v \in V}d_D^-(v) = \sum_{v \in V}d_D^+(v) = \varepsilon(D)$

2.4.4 回路

有向途径： $W=v_0a_1v_1a_2...v_{k-1}a_kv_k$ ，其中交替项为顶点和弧。那么 $W$ 就是有向途径。 $v_0$ 称为 $W$ 的起点， $v_k$ 称为 $W$ 的终点。 $k$ 称为 $W$ 的长。 $W$ 称为有向 $v_0,v_k)$ 途径。
有向闭途径：起点与终点相同的有向途径。
有向迹：弧各不相同的有向途径。
有向链(路)：顶点各不相同的有向途径。

2.4.5 强连通分支

强连通： $u, v$ 是有向图 $D$ 中的两个顶点，若存在 $(u, v)$ 路和 $(v, u)$ 路使得两点可以相互到达，则称 $u$ 和 $v$ 在图 $D$ 中是强连通的。
强连通分支/强连通有向图： $V (D)$ 的非空划分 $V_1V_2...V_\omega$ 在 $D$ 中所导出的子图 $D[V_1],D[V_2],...,D[D_\omega]$ 称为 $D$ 的强连通分支。若 $D$ 中只有一个强连通分支，则 $D$ 是强连通有向图。