前言：个人实验记录，仅供学习参考，实验报告别用我图

一、基础知识

1，为什么要进行插值：

有的时候我们要对图像进行放大，当然这里的放大是指放大图像的尺寸，例如把一个100x100大小的图像放大成200x200大小。其实在计算机里面，这个也就相当于把一个100x100的二维矩阵放大成一个200x200的矩阵。而插值，就是将矩阵上的这些位置填上数。缩小同理。

2，双线性插值原理：

我举例说明，如下图，我们要将下面的3x3矩阵放大成4x4的矩阵，这里算放大后矩阵的（2，2）出值应该是多少。

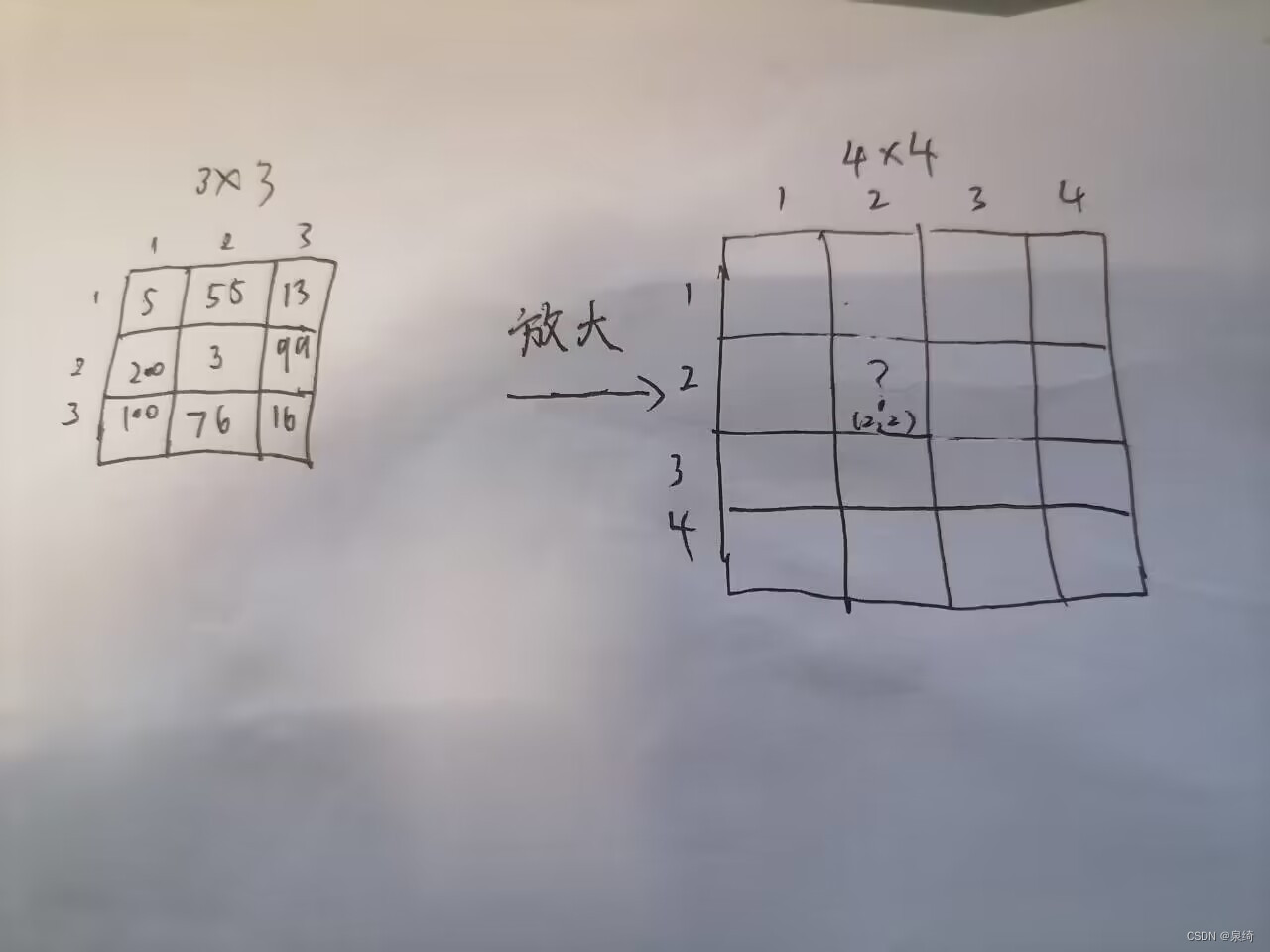
1）求出放大后图对应原图的位置：
我们不难得知：缩放图像素位置/对应原图上像素位置 = 缩放图尺寸/原图尺寸 = 缩放比例
于是可以求得：对应原图像素位置 = 缩放图像素位置x(原图尺寸/缩放图尺寸)

2)公式计算：
这里的i+u,j+v是上面通过计算后的原图的对应像素的横纵坐标。一般这个坐标都不是整数，我们通过matlab中的fix()函数（向下取整）来获取i,j的数据，再带入公式计算

像上图中的(2,2)位置，通过计算后可以得到它对应原图的下标是(1.5,1.5)。1.5向下取整是1，1.5-1=0.5，u,v都是0.5所以也就变成了：

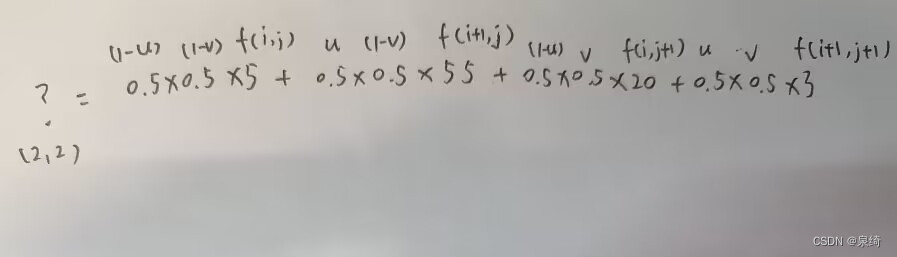
等于20.75，也就是我们在缩放图的(2,2)位置插入20.75，由于是图像，我们就要将其转为uint8数据
对图像的缩放就是从它的缩放图上遍历每个像素来插值。

3，最邻近插值：

这个就简单了，先求出缩放图像素的原图对应像素下标，对下标四舍五入，然后将四舍五入后的下标带入原图，插入缩放图像素就行了。

二、实验要求：

1．分别编程实现最近邻插值和双线性插值。

2．任意读入一幅图像，通过上诉两种插值方法，将图像放大2及2.5倍。

3. 显示结果，并进行比较。

三、实验记录：

1，双线性：

双线性插值函数double_line_value():

function [value] = double_line_value(S,i,j,k,maxi,maxj)
%此函数用于算双线性插值
%i,j表示坐标
u = i-fix(i);
i = fix(i);
%这里判断下标是否越界
if i < 1
    i = 1;
elseif i>maxi-1
    i = maxi-1;
end
v = j-fix(j);
j = fix(j);

if j < 1
    j = 1;
elseif j>maxj-1
    j = maxj-1;
end
%公式计算
%这里要注意，S图像里的值都是无符号数，
%要先转变数据类型再算
a = double(S(i,j,k));
b = double(S(i+1,j,k));
c = double(S(i,j+1,k));
d = double(S(i+1,j+1,k));

value = (1-u)*(1-v)*a+u*(1-v)*b+(1-u)*v*c+u*v*d;

end

对整个图像进行双线性插值函数img_to_double_line():

function [S1] = img_to_double_line(S,aim_height,aim_width)
% 这个函数用于对图像进行双线性插值
% 输入 图像S,目标高度，目标宽度
% 输出 图像Sd
[src_height,src_width,src_z] = size(S)
aim_z = src_z;

S1 = -1*ones(aim_height,aim_width,aim_z); %初始化结果图，将其中数据全变为-1
%遍历结果图，进行插值
for z = 1:aim_z
    for aimy = 1:aim_height
        for aimx=1:aim_width
            % 计算原图对应像素下标
            srcx = aimx*(src_width/aim_width);
            srcy = aimy*(src_height/aim_height);
            
            S1(aimy,aimx,z) = double_line_value(S,srcy,srcx,z,src_height,src_width);
        end
    end
end

[h,w,z]=size(S1);
S1 = uint8(S1);% 将其中数据转为uint8类型

end

2、最邻近：

最邻近插值函数recently_value():

function [value] = recently_value(S,i,j,k,maxi,maxj)
%最邻近插值法
%以下为先四舍五入，再插值
i = round(i);
if i < 1
    i = 1;
elseif i>maxi-1
    i = maxi-1;
end
j = round(j);
if j < 1
    j = 1;
elseif j>maxj-1
    j = maxj-1;
end
value = S(i,j,k);

end

对图像进行最邻近插值函数img_to_recently_value():

function [S2] = img_to_recently_value(S,aim_height,aim_width)
% 这个函数用于对图像进行最邻近插值
% 输入 原图片，目标高度，目标宽度
% 输出 图片S2
[src_height,src_width,src_z] = size(S)
aim_z = src_z;
S2 = -1*ones(aim_height,aim_width,aim_z);%初始化矩阵S2
for z = 1:aim_z
    for aimy = 1:aim_height
        for aimx=1:aim_width
            srcx = aimx*(src_width/aim_width);
            srcy = aimy*(src_height/aim_height);
            S2(aimy,aimx,z) = recently_value(S,srcy,srcx,z,src_height,src_width);
        end
    end
end
S2 = uint8(S2);
end

3，主程序：

clc;
clear;
% 实验四，双向线性插值和最邻近插值
S = imread('stone.jpg');
% S = rgb2gray(S);
[src_height,src_width,src_z] = size(S);%获得原图尺寸
figure;
imshow(S);title('原图');
for i=0:0.5:0.5
    c = 2+i;%放大比例
    %对放大后的尺寸四舍五入化为整数
    aim_height = round(c*src_height);
    aim_width = round(c*src_width);
    aim_z = src_z;

    S1 = img_to_double_line(S,aim_height,aim_width);
    S2 = img_to_recently_value(S,aim_height,aim_width);

    figure;
    imshow(S1);title(['双线性插值后图,放大',num2str(c),'倍']);

    figure;
    imshow(S2);title(['最近邻插值后图，放大',num2str(c),'倍']);
end

四、结果展示

1，原图：

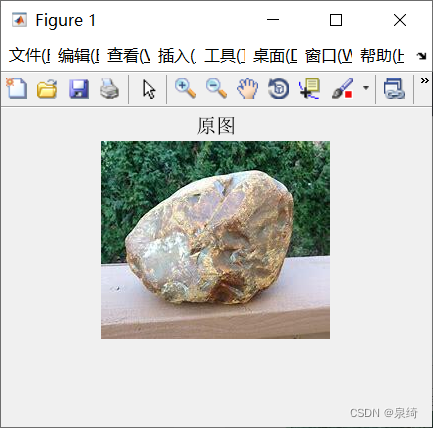
2，长宽各放大2倍：

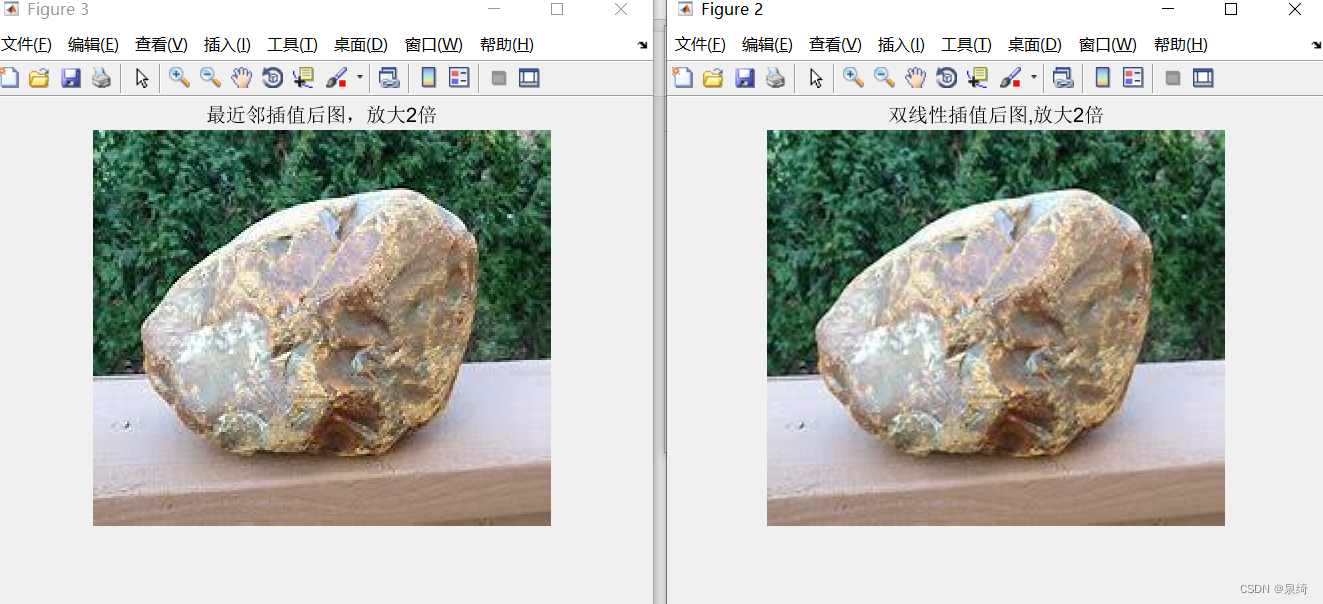
3，长宽各放大2.5倍：

五、反思总结与收获

1，注意数据类型

uint8还是很坑的,当我们进行有小数的运算时，最好将其数据转为double类型，最后再转回来。

2，比较双线性插值与最邻近插值

很明显，最邻近插值实现起来很简单，但是在图像上有边缘锯齿化表现，效果不佳。
双线性插值效果相对来说很好，生成的图像给人一种很圆润，很平滑的感觉。