215. 破译密码 - AcWing题库

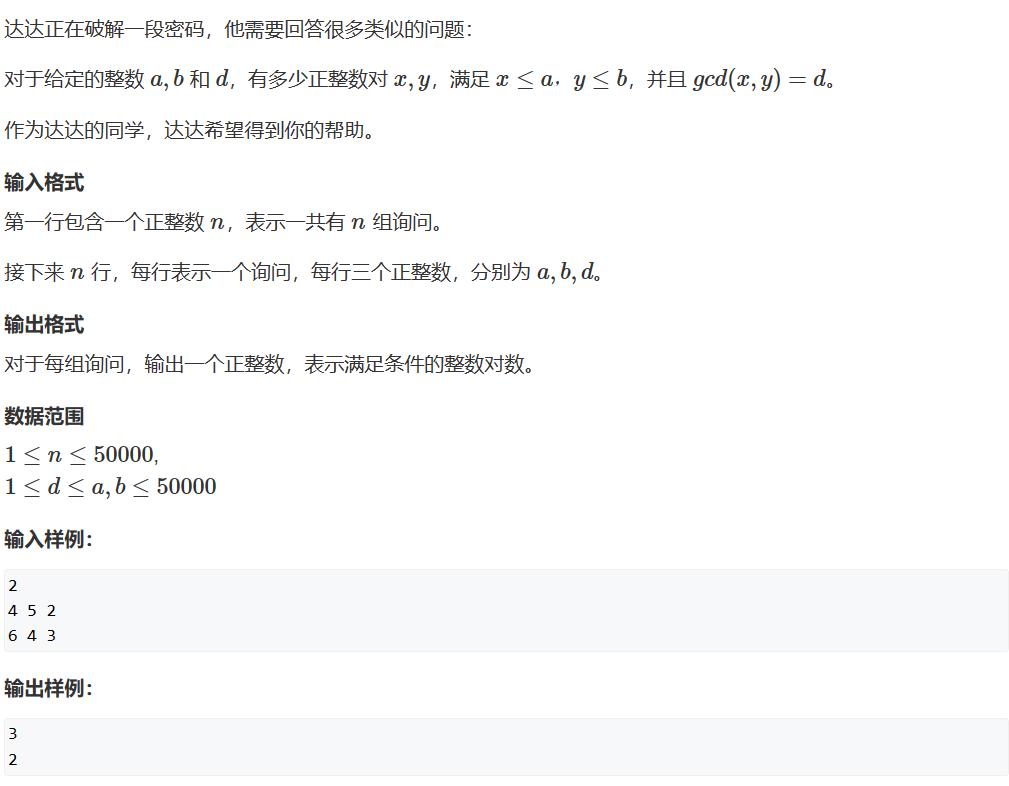
mobius函数：

一个数的分解质因数形式，某一个指数>1为0，质因数为奇数个为-1，偶数个为1 

mobius函数可以与容斥结合起来，比如mobius[2] = -1, mobius[3] = -1, mobius[2 * 3] = 1。对应容斥里面的加奇减偶。

如果a、b相同的话可以用欧拉函数做，不同的话就要另寻他法。

题目可以转化为,满足的对数

用容斥的思想：全部的组合-gcd为（2、3、5...）的+gcd为(6、10、15...)的...

设A = a / d, B = b / d

答案就为，因为质因子形式某一项指数>1的mobius函数为0，所以等同于之前的容斥

然后用整数分块的思想降低时间复杂度，在一个区间内(A/i) * (B/i)的值是固定的，可以看成一个常数，此时mobius函数可以用前缀和来降低时间复杂度。

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'
 
using namespace std;
 
typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;

const int N = 50010;

int a, b, d;
int primes[N], cnt;
bool st[N];
int mobius[N];

void init(int n)
{
	mobius[1] = 1;
	for(int i = 2; i <= n; i ++)
	{
		if(!st[i])
		{
			primes[cnt ++] = i;
			mobius[i] = -1;
		}
		for(int j = 0; primes[j] * i <= n; j ++)
		{
			st[primes[j] * i] = true;
			if(i % primes[j] == 0)
			{
				mobius[primes[j] * i] = 0;
				break;
			}
			mobius[primes[j] * i] = mobius[i] * -1;
		}
	}
	
	for(int i = 2; i <= n; i ++)mobius[i] += mobius[i - 1];
}

void solve()
{
	cin >> a >> b >> d;
	a /= d, b /= d;
	
	ll ans = 0;
	int n = min(a, b);
	for(int l = 1, r; l <= n; l = r + 1)
	{
		r = min(n, min(a / (a / l), b / (b / l)));
		ans += (ll)(mobius[r] - mobius[l - 1]) * (a / l) * (b / l);
	}
	cout << ans << endl;
}

int main()
{
	IOS
	init(N - 1);
	
	int _;
	cin >> _;
	while(_ --)
	{
		solve();
	}
	
	return 0;
}