ZKP学习笔记
ZK-Learning MOOC课程笔记
Lecture 4: SNARKs via Interactive Proofs (Justin Thaler)
4.3 Interactive proof design: Technical Preliminaries
-
SZDL Lemma
- Equal test (in multivariate polynomials)

- Equal test (in multivariate polynomials)
-
Low-Defree and Multilinear Extensions
-
Extensions

-
Multilinear Extensions

-
Examples

-

- f(0,0) = 1; f(0,1) = 2; f(1,0) = 8; f(1,1) = 10
-
f
~
(
0
,
0
)
=
1
;
f
~
(
0
,
1
)
=
2
;
f
~
(
1
,
0
)
=
8
;
f
~
(
1
,
1
)
=
10
\tilde{f}(0,0) = 1; \tilde{f}(0,1) = 2; \tilde{f}(1,0) = 8; \tilde{f}(1,1) = 10
f~(0,0)=1;f~(0,1)=2;f~(1,0)=8;f~(1,1)=10
-
f
~
(
x
1
,
x
2
)
=
(
1
−
x
1
)
(
1
−
x
2
)
+
2
(
1
−
x
1
)
x
2
+
8
x
1
(
1
−
x
2
)
+
10
x
1
x
2
\tilde{f}(x_1,x_2) = (1-x_1)(1-x_2)+2(1-x_1)x_2+8x_1(1-x_2)+10x_1x_2
f~(x1,x2)=(1−x1)(1−x2)+2(1−x1)x2+8x1(1−x2)+10x1x2: unique!
- (1-x_1)(1-x_2) term maps inputs (0,0) to 1
- 2(1-x_1)x_2 term maps inputs (0,1) to 2
- …
- Evaluating multilinear extensions quickly
- Use Lagrange Interpolation

-
δ
~
w
(
r
)
\tilde{\delta}_w(r)
δ~w(r) maps (0,0) to 1; others to 0
4.4 The Sum-check Protocol [LFKN90]
-
Input: V given oracle access to a l-variate polynomial g over filed F.
- Prover负责计算,并把计算结果和proof给Verifier。
- Verifier验证计算结果的正确性
-
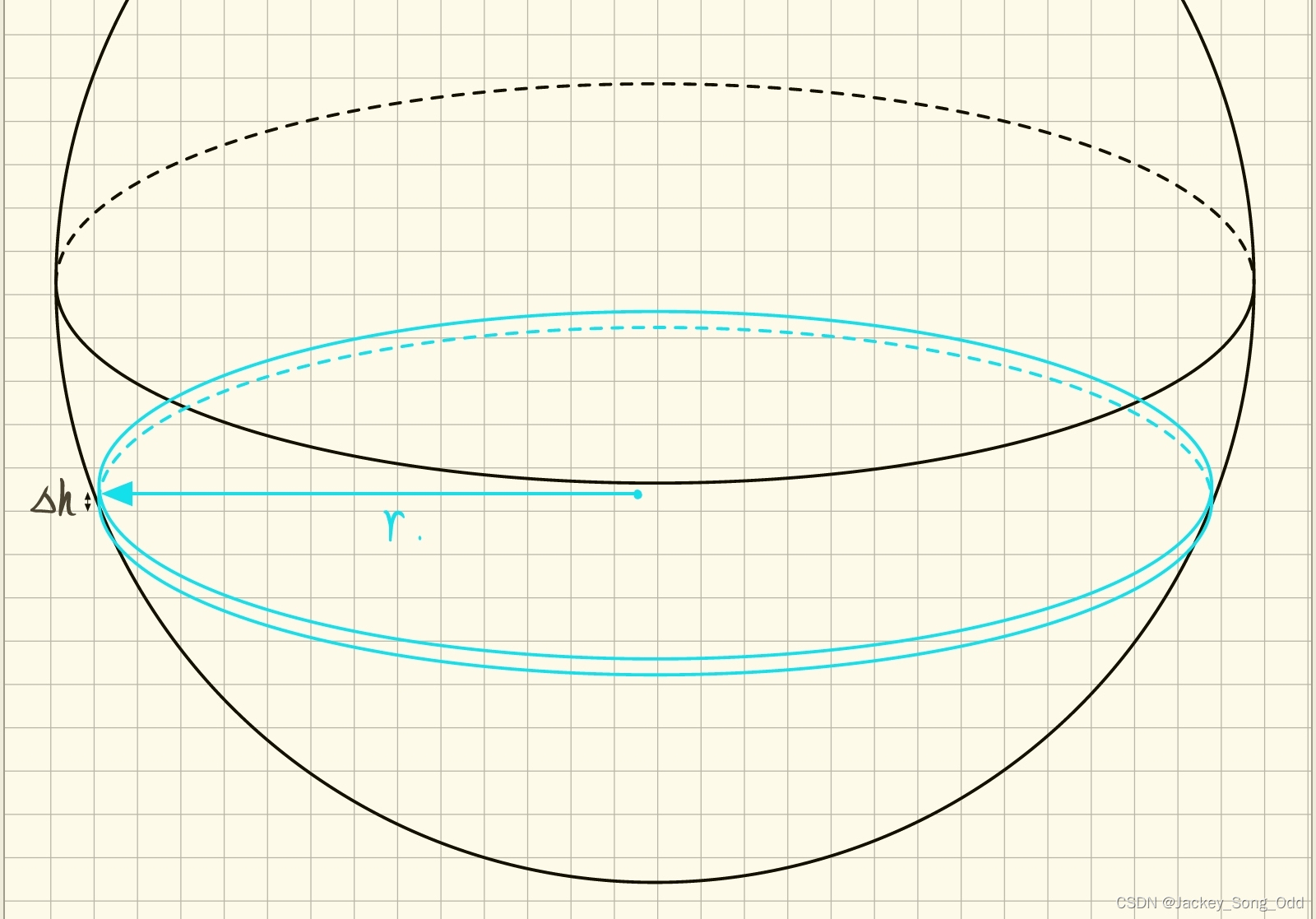
Goal: compute the quantity
- Σ b 1 ∈ { 0 , 1 } Σ b 2 ∈ { 0 , 1 } … Σ b l ∈ { 0 , 1 } g ( b 1 , … , b l ) \Sigma_{b1\in\{0,1\}} \Sigma_{b2\in\{0,1\}} \dots \Sigma_{bl\in\{0,1\}} g(b_1,\dots,b_l) Σb1∈{0,1}Σb2∈{0,1}…Σbl∈{0,1}g(b1,…,bl)
-
最简单的方法,verifier问prover每个点的值然后加起来,需要 2 l 2^l 2l次
-
Sum-check Protocol

- s1 is the prover actually sent and H1 is what the prover would send if the prover is honest
- H1 is equal to the true answer except it have been cut off the first sum
- H1 is a univariate polynomial


- s1 is the prover actually sent and H1 is what the prover would send if the prover is honest
-
Analysis of the sum-check protocol
-
Completeness
-
Soundness

-
Costs of the sum-check protocol

-
-
Application: Counting Triangles
- Input A ∈ 0 , 1 n × n A \in {0,1}^{n \times n} A∈0,1n×n, representing the adjacency matrix of a graph
- Output:
Σ
i
,
j
,
k
∈
[
n
]
3
A
i
j
A
j
k
A
i
k
\Sigma_{i,j,k \in[n]^3} A_{ij}A_{jk}A_{ik}
Σi,j,k∈[n]3AijAjkAik
- Time cost in matrix-multiplication: n 2.37 n^{2.37} n2.37
- The Protocol:
- View A as a function mapping
{
0
,
1
}
log
n
×
{
0
,
1
}
log
n
\{0,1\}^{\log n} \times \{0,1\}^{\log n}
{0,1}logn×{0,1}logn to F

- View A as a function mapping
{
0
,
1
}
log
n
×
{
0
,
1
}
log
n
\{0,1\}^{\log n} \times \{0,1\}^{\log n}
{0,1}logn×{0,1}logn to F

- Cost
- Communication: O ( log n ) O(\log n) O(logn)
- V runtime is O ( n 2 ) O(n^2) O(n2)
- P runtime is O ( n 3 ) O(n^3) O(n3)
- A SNARK for circuit-satisfiability
-
SNARKs for circuit-satisfiability

-
Viewing a transcript T as a function with domain { 0 , 1 } log S \{0,1\}^{\log S} {0,1}logS

-
4.5 The polynomial IOP underlying the SNARK
-
The start of the polynomial IOP

- Intuition for why h is a useful object for P to send
- Think of h as a distance-amplified encoding of the transcript T
- the domain of T is 0 , 1 log S {0,1}^{\log S} 0,1logS. The domain of h is F log S F^{\log S} FlogS
- Even tiny differences in transcripts can get blown up by the extension polynomials into easily detectable differences, in particular that are detectable even by a verifier that is only allowed to evaluate those extension polynomials at a single point.
- Think of h as a distance-amplified encoding of the transcript T
- Intuition for why h is a useful object for P to send
-
Two-step plan of attack (这部分没听懂QAQ)




- The polynomial IOP for circuit-satisfiability