文章目录
- 统计学习方法 隐马尔可夫模型
- 基本概念
- 概率计算问题
- 直接计算法
- 前向算法
- 后向算法
- 前向概率和后向概率
- 学习问题
- 监督学习算法
- Baum-Welch 算法
- E 步
- M 步
- 参数估计公式
- 算法描述
- 解码问题
- 近似算法
- Viterbi 算法
统计学习方法 隐马尔可夫模型
读李航的《统计学习方法》时,关于隐马尔可夫模型的笔记
隐马尔可夫模型(hidden Markov model, HMM)是可用于标注问题的统计学习模型,属于生成模型。
基本概念
隐马尔可夫模型:在 Markov 链的基础上,随机生成不可观测的状态序列,再由每个状态生成一个观测,产生观测序列,序列的每个位置可看成一个时刻。
隐马尔可夫模型由初始概率分布 π \pi π 、状态转移概率分布 A A A 以及观测概率分布 B B B 确定,符号定义如下:
设
Q
Q
Q 是所有可能状态的集合,
V
V
V 是所有可能观测的集合:
Q
=
{
q
1
,
q
2
,
⋯
,
q
N
}
,
V
=
{
v
1
,
v
2
,
⋯
,
v
M
}
Q=\set{q_1,\,q_2,\,\cdots,\,q_N},\quad V=\set{v_1,\,v_2,\,\cdots,\,v_M}
Q={q1,q2,⋯,qN},V={v1,v2,⋯,vM}
N
N
N 是可能的状态数,
M
M
M 是可能的观测数。
I
I
I 是长度为
T
T
T 的状态序列,
O
O
O 是对应的观测序列:
I
=
{
i
1
,
i
2
,
⋯
,
i
T
}
,
O
=
(
o
1
,
o
2
,
⋯
,
o
T
)
I=\set{i_1,\,i_2,\,\cdots,\,i_T},\quad O=(o_1,\,o_2,\,\cdots,\,o_T)
I={i1,i2,⋯,iT},O=(o1,o2,⋯,oT)
A
A
A 是状态转移概率矩阵,跟 Markov 链的定义是一样的:
A
=
[
a
i
j
]
N
×
N
A=[a_{ij}]_{N\times N}
A=[aij]N×N
其中
a
i
j
a_{ij}
aij 代表从状态
q
i
q_i
qi 转移到状态
q
j
q_j
qj 的概率:
a
i
j
=
P
(
i
t
+
1
=
q
j
∣
i
t
=
q
i
)
,
i
=
1
,
2
,
⋯
,
N
;
j
=
1
,
2
,
⋯
,
N
a_{ij}=P(i_{t+1}=q_j|i_{t}=q_i),\quad i=1,\,2,\,\cdots,\,N;\quad j=1,\,2,\,\cdots,\,N
aij=P(it+1=qj∣it=qi),i=1,2,⋯,N;j=1,2,⋯,N
B
B
B 是观测概率矩阵:
B
=
[
b
j
(
k
)
]
N
×
M
B=[b_j(k)]_{N\times M}
B=[bj(k)]N×M
其中
b
j
(
k
)
b_j(k)
bj(k) 代表状态
q
j
q_j
qj 产生观测结果
v
k
v_k
vk 的概率:
b
j
(
k
)
=
P
(
o
t
=
v
k
∣
i
t
=
q
j
)
,
k
=
1
,
2
,
⋯
,
M
;
j
=
1
,
2
,
⋯
,
N
;
b_j(k)=P(o_t=v_k|i_t=q_j),\quad k=1,\,2,\,\cdots,\,M; \quad j=1,\,2,\,\cdots,\,N;
bj(k)=P(ot=vk∣it=qj),k=1,2,⋯,M;j=1,2,⋯,N;
π
\pi
π 是初始概率向量:
π
=
(
π
i
)
\pi=(\pi_i)
π=(πi)
其中
π
i
\pi_i
πi 代表初始时刻(
t
=
1
t=1
t=1)处于状态
q
i
q_i
qi 的概率:
π
i
=
P
(
i
1
=
q
i
)
,
i
=
1
,
2
,
⋯
,
N
\pi_i=P(i_1=q_i),\quad i=1,\,2,\,\cdots,\,N
πi=P(i1=qi),i=1,2,⋯,N
即隐马尔可夫模型
λ
\lambda
λ 可以表示为三元组:
λ
=
(
π
,
A
,
B
)
\lambda=(\pi,\,A,\,B)
λ=(π,A,B)
隐马尔可夫模型的基本假设:有两个基本假设
- 齐次 Markov 性:任意时刻 t t t 的状态只依赖于前一时刻状态,而与其他时刻的状态及观测无关,与时刻 t t t 也无关:
P ( i t ∣ i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , i = 1 , 2 , ⋯ , T P(i_{t}|i_{t-1},\,o_{t-1},\,\cdots,\,i_1,\,o_1)=P(i_t|i_{t-1}),\quad i=1,\,2,\,\cdots,\,T P(it∣it−1,ot−1,⋯,i1,o1)=P(it∣it−1),i=1,2,⋯,T
- 观测独立性:任意时刻的观测只依赖于该时刻所处的 Markov 链上的状态,与其他任何观测及状态无关:
P ( o t ∣ i T , o T , ⋯ , i t + 1 , o t + 1 , i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( o t ∣ i t ) P(o_t|i_T,\,o_T,\,\cdots,\,i_{t+1},\,o_{t+1},\,i_{t-1},\,o_{t-1},\,\cdots,\,i_1,\,o_1)=P(o_t|i_t) P(ot∣iT,oT,⋯,it+1,ot+1,it−1,ot−1,⋯,i1,o1)=P(ot∣it)
标注问题:对于标注问题,我们可以认为标注问题的数据是由 HMM 生成的,并且状态对应着标记,只要通过学习和预测算法就可以进行标注。
例(盒子和球模型):有四个盒子,每个盒子里装有若干红、白两种颜色的球:
box
1
box
2
box
3
box
4
red ball
5
3
6
8
white ball
5
7
4
2
\begin{array}{ccccc} \hline & \text{box}1 & \text{box}2 & \text{box}3 & \text{box}4 \\ \hline \text{red ball} & 5 & 3 & 6 & 8\\ \hline \text{white ball} & 5 & 7 & 4 & 2\\ \hline \end{array}
red ballwhite ballbox155box237box364box482
按照以下抽球方式,产生一个颜色的观测序列:
- 开始时,从四个盒子中等概率地选择一个,有放回地取出一个球并记录颜色;
- 然后转移到下一个盒子:如果是盒子 1,则必转移到盒子 2;如果是盒子 2 或盒子 3,则分别以 0.4 和 0.6 的概率转移到左边和右边的盒子;如果是盒子 4,则各以 0.5 的概率留在盒子 4 或转移到盒子 3;
- 重复,比如进行 5 次,得到一个观测序列:
O = { r , r , w , w , r } O=\set{r,\,r,\,w,\,w,\,r} O={r,r,w,w,r}
这个过程中,观察者只能观测到球的颜色,而并不知道球是从哪个盒子里取出的。因此盒子对应状态,即:
Q
=
{
1
,
2
,
3
,
4
}
,
N
=
4
Q=\set{1,\,2,\,3,\,4},\quad N=4
Q={1,2,3,4},N=4
球的颜色为观测集合:
V
=
{
r
,
w
}
,
M
=
2
V=\set{r,\,w},\quad M=2
V={r,w},M=2
初始概率分布为:
π
=
(
0.25
,
0.25
,
0.25
,
0.25
)
T
\pi=(0.25,\,0.25,\,0.25,\,0.25)^T
π=(0.25,0.25,0.25,0.25)T
状态转移概率分布为:
A
=
[
0
1
0
0
0.4
0
0.6
0
0
0.4
0
0.6
0
0
0.5
0.5
]
A=\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0.4 & 0 & 0.6 & 0 \\ 0 & 0.4 & 0 & 0.6 \\ 0 & 0 & 0.5 & 0.5 \\ \end{bmatrix}
A=
00.400100.4000.600.5000.60.5
观测概率分布为:
B
=
[
0.5
0.5
0.3
0.7
0.6
0.4
0.8
0.2
]
B=\begin{bmatrix} 0.5 & 0.5 \\ 0.3 & 0.7\\ 0.6 & 0.4\\ 0.8 & 0.2 \\ \end{bmatrix}
B=
0.50.30.60.80.50.70.40.2
三个基本问题:给定 HMM,随机生成一个观测序列是很容易的。但还有以下三个不那么明显的问题:
- 概率计算问题:给定模型和观测序列,计算该模型产生该观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) ;
- 学习问题:给定观测序列,估计模型参数,使得 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) 最大,即用极大似然估计的方法估计参数;
- 预测问题:也称解码问题,已知模型参数和观测序列,求使得条件概率 P ( I ∣ O ) P(I|O) P(I∣O) 最大的状态序列 I = ( i 1 , i 2 , ⋯ , i T ) I=(i_1,\,i_2,\,\cdots,\,i_T) I=(i1,i2,⋯,iT) ,即给定观测序列,求出最有可能的对应的状态序列。
概率计算问题
概率计算问题是指,给定模型和观测序列,计算该模型产生该观测序列的概率。
直接计算法
算法:直接枚举所有可能的长度为 T T T 的状态序列,然后求出各状态序列产生该观测序列的概率,最后求和。
出现状态序列
I
=
(
i
1
,
i
2
,
⋯
,
i
T
)
I=(i_1,\,i_2,\,\cdots,\,i_T)
I=(i1,i2,⋯,iT) 的概率为:
P
(
I
∣
λ
)
=
π
i
1
a
i
1
i
2
a
i
2
i
3
⋯
a
i
T
−
1
i
T
P(I|\lambda)=\pi_{i_1}a_{i_1i_2}a_{i_2i_3}\cdots a_{i_{T-1}i_T}
P(I∣λ)=πi1ai1i2ai2i3⋯aiT−1iT
对于该状态序列,产生观测
O
=
(
o
1
,
o
2
,
⋯
o
T
)
O=(o_1,\,o_2,\,\cdots o_T)
O=(o1,o2,⋯oT) 的概率为:
P
(
O
∣
I
,
λ
)
=
b
i
1
(
o
1
)
b
i
2
(
o
2
)
⋯
b
i
T
(
o
T
)
P(O|I,\,\lambda)=b_{i_1}(o_1)b_{i_2}(o_2)\cdots b_{i_T}(o_T)
P(O∣I,λ)=bi1(o1)bi2(o2)⋯biT(oT)
则该观测序列出现的总的概率为:
P
(
O
∣
λ
)
=
∑
I
P
(
O
∣
I
,
λ
)
P
(
I
∣
λ
)
=
∑
i
1
,
i
2
,
⋯
,
i
T
π
i
1
b
i
1
(
o
1
)
a
i
1
i
2
b
i
2
(
o
2
)
a
i
2
i
3
⋯
a
i
T
−
1
i
T
b
i
T
(
o
T
)
\begin{aligned} P(O|\lambda)=&\, \sum_I P(O|I,\,\lambda)P(I|\lambda) \\ =&\, \sum_{i_1,\,i_2,\,\cdots,\,i_T}\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)a_{i_2i_3}\cdots a_{i_{T-1}i_T}b_{i_T}(o_T) \end{aligned}
P(O∣λ)==I∑P(O∣I,λ)P(I∣λ)i1,i2,⋯,iT∑πi1bi1(o1)ai1i2bi2(o2)ai2i3⋯aiT−1iTbiT(oT)
但是这个算法的时间复杂度为
O
(
T
N
T
)
O(TN^T)
O(TNT) ,是指数级别的。
前向算法
前向概率:给定模型
λ
\lambda
λ ,定义前向概率为,到时刻
t
t
t 时,前面出现的观测序列为
O
[
0
,
t
]
=
(
0
1
,
o
2
,
⋯
,
o
t
)
O[0,\,t]=(0_1,\,o_2,\,\cdots,\,o_t)
O[0,t]=(01,o2,⋯,ot) ,而此时状态正好为
q
i
q_i
qi 的概率,记为:
α
t
(
i
)
=
P
(
o
1
,
o
2
,
⋯
,
o
t
,
i
t
=
q
t
∣
λ
)
\alpha_t(i)=P(o_1,\,o_2,\,\cdots,\,o_t,\,i_t=q_t|\lambda)
αt(i)=P(o1,o2,⋯,ot,it=qt∣λ)
可以想到,如果知道了前一时刻
t
−
1
t-1
t−1 所有状态的前向概率,则可以得到下一时刻
t
t
t 任一状态
q
i
q_i
qi 的前向概率,只需要前向概率乘以状态转移概率,再乘以产生
o
t
o_t
ot 的概率,最后求和即可:
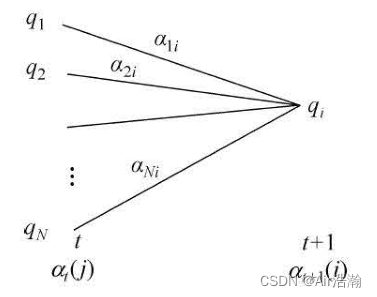
并且,知道了 T T T 时刻所有状态的前向概率以后,将所有状态的前向概率求和即可得到
算法:观测序列概率的前向算法
- 输入:HMM λ \lambda λ ,观测序列 O O O ;
- 输出:产生该观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) ;
- 初值:
α 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , ⋯ , N \alpha_1(i)=\pi_ib_i(o_1),\quad i=1,\,2,\,\cdots,\,N α1(i)=πibi(o1),i=1,2,⋯,N
- 递推:对于 t = 1 , 2 , ⋯ , T − 1 t=1,\,2,\,\cdots,\,T-1 t=1,2,⋯,T−1 ,递推地计算后一时刻的前向概率:
α t + 1 ( i ) = b i ( o t + 1 ) ∑ j = 1 N α t ( j ) a j i \alpha_{t+1}(i)=b_i(o_{t+1})\sum_{j=1}^{N}\alpha_t(j)a_{ji} αt+1(i)=bi(ot+1)j=1∑Nαt(j)aji
- 终止:求 T T T 时刻所有状态的前向概率的和:
P ( O ∣ λ ) = ∑ 1 N α T ( i ) P(O|\lambda)= \sum_{1}^{N} \alpha_T(i) P(O∣λ)=1∑NαT(i)
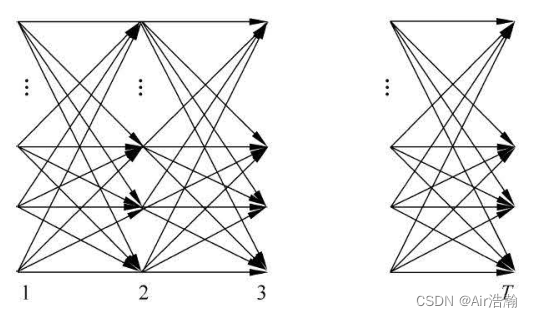
整个计算过程即如下的 DAG(有点像 Bellman-Ford 的计算路径),想象一下,其实直接算法的计算路径就如同一颗以状态数 N N N 为子节点数的 N N N 叉树,而前向算法则是将每一层重复节点进行了合并(就如同 DP 优化暴力算法一样),因此得到的时间复杂度为 O ( N 2 T ) O(N^2T) O(N2T) :
例(盒子和球模型):状态集合为
Q
=
{
1
,
2
,
3
}
Q=\set{1,\,2,\,3}
Q={1,2,3},观测集合为
V
=
{
r
,
w
}
V=\set{r,\,w}
V={r,w} ,
A
=
[
0.5
0.2
0.3
0.3
0.5
0.2
0.2
0.3
0.5
]
B
=
[
0.5
0.5
0.4
0.6
0.7
0.3
]
π
=
[
0.2
0.4
0.4
]
A=\begin{bmatrix} 0.5 & 0.2 & 0.3\\ 0.3 & 0.5 & 0.2\\ 0.2 & 0.3 & 0.5\\ \end{bmatrix} \quad B=\begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6\\ 0.7 & 0.3\\ \end{bmatrix} \quad \pi=\begin{bmatrix} 0.2\\ 0.4\\ 0.4\\ \end{bmatrix}
A=
0.50.30.20.20.50.30.30.20.5
B=
0.50.40.70.50.60.3
π=
0.20.40.4
假设得到的观测序列为
O
=
(
r
,
w
,
r
)
O=(r,\,w,\,r)
O=(r,w,r) ,则前向概率为:
T
1
2
3
box
1
0.10
0.077
0.04187
box
2
0.16
0.1104
0.03551
box
3
0.28
0.0606
0.05284
\begin{array}{cccc} \hline T & 1 & 2 & 3 \\ \hline \text{box}1 & 0.10 & 0.077 & 0.04187 \\ \hline \text{box}2 & 0.16 & 0.1104 & 0.03551\\ \hline \text{box}3 & 0.28 & 0.0606 & 0.05284 \\ \hline \end{array}
Tbox1box2box310.100.160.2820.0770.11040.060630.041870.035510.05284
这个表格的计算顺序是一列一列计算的,最后一列的和即为所求结果:
P
(
O
∣
λ
)
=
0.13022
P(O|\lambda)=0.13022
P(O∣λ)=0.13022
后向算法
后向概率:给定模型
λ
\lambda
λ ,后向概率定义为,时刻
t
t
t 为状态
q
i
q_i
qi 的条件下,后续的观测序列正好是
O
[
t
+
1
,
T
]
=
(
o
t
+
1
,
o
t
+
2
,
⋯
,
o
T
)
O[t+1,\,T]=(o_{t+1},\,o_{t+2},\,\cdots,\,o_{T})
O[t+1,T]=(ot+1,ot+2,⋯,oT) 的概率:
β
t
(
i
)
=
P
(
o
t
+
1
,
o
t
+
1
,
⋯
,
o
T
∣
i
t
=
q
i
,
λ
)
\beta_t(i)=P(o_{t+1},\,o_{t+1},\,\cdots,\,o_T|i_t=q_i,\,\lambda)
βt(i)=P(ot+1,ot+1,⋯,oT∣it=qi,λ)
可以想到,如果知道
t
+
1
t+1
t+1 时刻所有状态的后向概率,那么就可以求得
t
t
t 时刻任一状态的后向概率,只需要将后向概率乘以状态转移概率,再乘上产生观测为
o
t
+
1
o_{t+1}
ot+1 的概率,最后求和即可:
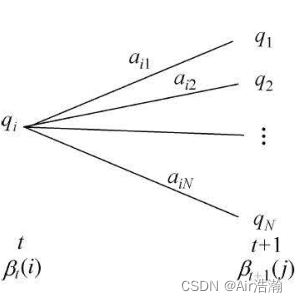
注意:后向概率 β t ( i ) \beta_t(i) βt(i) 中并没有包含 t t t 时刻的观测 o t o_t ot 出现的概率。
算法:观测序列概率的后向算法
- 输入:HMM λ \lambda λ ,观测序列 O O O ;
- 输出:产生该观测序列的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) ;
- 初值:时刻 T T T 以后没有观测了,所以可以认为处于每个状态的后向概率是 1:
β T ( i ) = 1 , i = 1 , 2 , ⋯ , N \beta_T(i)=1,\quad i=1,\,2,\,\cdots,\,N βT(i)=1,i=1,2,⋯,N
- 递归:对于 t = T − 1 , T − 2 , ⋯ , 1 t=T-1,\,T-2,\,\cdots,\,1 t=T−1,T−2,⋯,1 递归地计算前一时刻的后向概率:
β t ( i ) = ∑ j = 1 N a i j b j ( o t + 1 ) β t + 1 ( j ) , i = 1 , 2 , ⋯ , N \beta_t(i)=\sum_{j=1}^{N}a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j),\quad i=1,\,2,\,\cdots,\,N βt(i)=j=1∑Naijbj(ot+1)βt+1(j),i=1,2,⋯,N
- 求和:最后时刻 t = 1 t=1 t=1 时,后向概率要乘以初始分布位于该状态的概率,以及产生第一个观测的概率,并求和:
P ( O ∣ λ ) = ∑ i = 1 N π i b i β 1 ( i ) P(O|\lambda)=\sum_{i=1}^{N}\pi_ib_i\beta_{1}(i) P(O∣λ)=i=1∑Nπibiβ1(i)
前向概率和后向概率
状态转移的过程可以看成是如下图的某条路径:

经过某个点的概率:利用前向和后向概率的定义,可以将观测序列概率
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ) 统一写成:
P
(
O
∣
λ
)
=
∑
j
=
1
N
α
t
(
j
)
β
t
(
j
)
,
t
=
1
,
2
,
⋯
,
T
−
1
P(O|\lambda)=\sum\limits_{j=1}^N \alpha_t(j)\beta_t(j),\quad t=1,\,2,\,\cdots,\,T-1
P(O∣λ)=j=1∑Nαt(j)βt(j),t=1,2,⋯,T−1
可以理解成,我们任意选择其中一层,其中共有
N
N
N 个节点。对于每个节点,
a
t
(
i
)
a_t(i)
at(i) 代表产生前面的观测序列后到达该节点的概率,
β
t
(
j
)
\beta_{t}(j)
βt(j) 代表从该节点出发得到剩余的观测序列的概率。所有这些乘在一起则代表:给定模型
λ
\lambda
λ ,在
t
t
t 时刻正好经过该节点并且最终也正好得到
O
O
O 的概率
即:
P
(
i
t
=
q
i
,
O
∣
λ
)
=
α
t
(
j
)
β
t
(
j
)
P(i_t=q_i,\,O|\lambda)=\alpha_t(j)\beta_t(j)
P(it=qi,O∣λ)=αt(j)βt(j)
而给定模型
λ
\lambda
λ 和观测序列
O
O
O ,在时刻
t
t
t 处于状态
q
i
q_i
qi 的概率,记为:
γ
t
(
i
)
=
P
(
i
t
=
q
i
∣
O
,
λ
)
=
P
(
i
t
=
q
i
,
O
∣
λ
)
P
(
O
∣
λ
)
=
α
t
(
j
)
β
t
(
j
)
∑
j
=
1
N
α
t
(
j
)
β
t
(
j
)
\begin{aligned} \gamma_t(i)=&\, P(i_t=q_i|O,\,\lambda) \\ =&\ \frac{P(i_t=q_i,\,O|\lambda)}{P(O|\lambda)} \\ =&\, \frac{\alpha_t(j)\beta_t(j)}{\sum\limits_{j=1}^N \alpha_t(j)\beta_t(j)} \end{aligned}
γt(i)===P(it=qi∣O,λ) P(O∣λ)P(it=qi,O∣λ)j=1∑Nαt(j)βt(j)αt(j)βt(j)
经过某条边的概率:利用前向和后向概率的定义,可以将观测序列概率
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ) 统一写成:
P
(
O
∣
λ
)
=
∑
i
=
1
N
∑
j
=
1
N
a
t
(
i
)
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
,
t
=
1
,
2
,
⋯
,
T
−
1
P(O|\lambda)=\sum_{i=1}^{N}\sum_{j=1}^{N} a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j),\quad t=1,\,2,\,\cdots,\,T-1
P(O∣λ)=i=1∑Nj=1∑Nat(i)aijbj(ot+1)βt+1(j),t=1,2,⋯,T−1
可以理解成,我们任意选择相邻的某两层节点,其中共有
N
2
N^2
N2 条边。对于每条边,
a
t
(
i
)
a_t(i)
at(i) 代表产生前面的观测序列后到达左节点的概率,
a
i
j
a_{ij}
aij 代表从左节点转移到右节点的概率,
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
b_{j}(o_{t+1})\beta_{t+1}(j)
bj(ot+1)βt+1(j) 代表从右节点出发得到剩余的观测序列的概率。所有这些乘在一起则代表:给定模型
λ
\lambda
λ ,在
t
→
t
+
1
t\to t+1
t→t+1 时刻正好经过这条边并且最终也正好得到
O
O
O 的概率,即:
P
(
i
t
=
q
i
,
i
t
+
1
=
q
j
,
O
∣
λ
)
=
a
t
(
i
)
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
P(i_t=q_i,\,i_{t+1}=q_{j},\,O|\lambda)=a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)
P(it=qi,it+1=qj,O∣λ)=at(i)aijbj(ot+1)βt+1(j)
对相邻的某两层节点之间所有边,将经过每条边的概率求和,即得到
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ) 。
而给定模型
λ
\lambda
λ 和观测序列
O
O
O , 在
t
→
t
+
1
t\to t+1
t→t+1 时刻正好经过某条边的概率为:
ξ
t
(
i
,
j
)
=
P
(
i
t
=
q
i
,
i
t
+
1
=
q
j
∣
O
,
λ
)
=
P
(
i
t
=
q
i
,
i
t
+
1
=
q
j
,
O
∣
λ
)
P
(
O
∣
λ
)
=
a
t
(
i
)
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
∑
i
=
1
N
∑
j
=
1
N
a
t
(
i
)
a
i
j
b
j
(
o
t
+
1
)
β
t
+
1
(
j
)
\begin{aligned} \xi_t(i,\,j)=&\, P(i_t=q_i,\,i_{t+1}=q_j|O,\,\lambda) \\ =&\, \frac{P(i_t=q_i,\,i_{t+1}=q_j,\,O|\lambda)}{P(O|\lambda)} \\ =&\, \frac{a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)}{\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N} a_t(i)a_{ij}b_{j}(o_{t+1})\beta_{t+1}(j)} \end{aligned}
ξt(i,j)===P(it=qi,it+1=qj∣O,λ)P(O∣λ)P(it=qi,it+1=qj,O∣λ)i=1∑Nj=1∑Nat(i)aijbj(ot+1)βt+1(j)at(i)aijbj(ot+1)βt+1(j)
学习问题
学习问题是指,给定观测序列,估计模型参数,使得 P ( O ∣ λ ) P(O|\lambda) P(O∣λ) 最大,即用极大似然估计的方法估计参数。
监督学习算法
就是使用完全数据,假设训练数据包含
S
S
S 个长度相同的观测序列和对应的状态序列,那么可以使用极大似然估计法来估计 HMM 的参数:
train_data
=
{
(
O
1
,
I
1
)
,
(
O
1
,
I
2
)
,
⋯
,
(
O
S
,
I
S
)
}
\text{train\_data}=\set{(O_1,\,I_1),\,(O_1,\,I_2),\,\cdots,\,(O_S,\,I_S)}
train_data={(O1,I1),(O1,I2),⋯,(OS,IS)}
- 转移概率 a i j a_{ij} aij 的估计:就是从状态 q i q_i qi 出发的转移中,转移到 q j q_j qj 的频率;设样本中从状态 q i q_i qi 转移到状态 q j q_j qj 的频数为 A i j A_{ij} Aij ,则状态转移概率 a i j a_{ij} aij 的估计是:
a ^ i j = A i j ∑ j = 1 N A i j , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , N \hat{a}_{ij}=\frac{A_{ij}}{\sum\limits_{j=1}^N A_{ij}},\quad i=1,\,2,\,\cdots,\,N;\quad j=1,\,2,\,\cdots,\,N a^ij=j=1∑NAijAij,i=1,2,⋯,N;j=1,2,⋯,N
- 观测概率 b j ( k ) b_j(k) bj(k) 的估计:就是处于状态 q j q_j qj 时,产生观测 v k v_k vk 的频率;设样本中处于状态 q j q_j qj 时,产生观测 v k v_k vk 的频数为 B j k B_{jk} Bjk ,则观测概率 b j ( k ) b_j(k) bj(k) 的估计为:
b ^ j ( k ) = B j k ∑ k = 1 M B j k , j = 1 , 2 , ⋯ , N ; k = 1 , 2 , ⋯ , M \hat{b}_j(k)=\frac{B_{jk}}{\sum\limits_{k=1}^{M}B_{jk}},\quad j=1,\,2,\,\cdots,\,N; \quad k=1,\,2,\,\cdots,\,M b^j(k)=k=1∑MBjkBjk,j=1,2,⋯,N;k=1,2,⋯,M
- 初始状态概率 π i \pi_i πi 的估计:就是 S S S 个样本中初始状态为 q i q_i qi 的频率;
Baum-Welch 算法
Baum-Welch 算法是 EM 算法在 HMM 的参数估计中的具体实现。
E 步
这里
O
=
(
o
1
,
o
2
,
⋯
,
o
T
)
O=(o_1,\,o_2,\,\cdots,\,o_T)
O=(o1,o2,⋯,oT) 相当于 EM 算法中的
Y
Y
Y ,
I
=
(
i
1
,
i
2
,
⋯
,
i
T
)
I=(i_1,\,i_2,\,\cdots,\,i_T)
I=(i1,i2,⋯,iT) 相当于 EM 算法中的
Z
Z
Z ,而
λ
=
(
π
,
A
,
B
)
\lambda=(\pi,\,A,\,B)
λ=(π,A,B) 相当于 EM 算法中的
θ
\theta
θ 。因此,完全数据的对数似然函数为:
log
P
(
O
,
I
∣
λ
)
\log P(O,\,I|\lambda)
logP(O,I∣λ)
Q
Q
Q 函数为:
Q
(
λ
∣
λ
^
)
=
E
I
[
log
P
(
O
,
I
∣
λ
)
∣
O
,
λ
^
]
=
∑
I
log
P
(
O
,
I
∣
λ
)
P
(
I
∣
λ
^
)
=
∑
I
log
P
(
O
,
I
∣
λ
)
P
(
O
,
I
∣
λ
^
)
P
(
O
∣
λ
^
)
\begin{aligned} Q(\lambda|\hat\lambda) =&\, E_I[\log P(O,\,I|\lambda)|O,\,\hat\lambda]\\ =&\, \sum_I \log P(O,\,I|\lambda)P(I|\hat\lambda) \\ =&\, \sum_I \log P(O,\,I|\lambda)\frac{P(O,\,I|\hat\lambda)}{P(O|\hat\lambda)} \end{aligned}
Q(λ∣λ^)===EI[logP(O,I∣λ)∣O,λ^]I∑logP(O,I∣λ)P(I∣λ^)I∑logP(O,I∣λ)P(O∣λ^)P(O,I∣λ^)
因为
Q
Q
Q 函数的变量为
λ
\lambda
λ ,
1
P
(
O
∣
λ
^
)
\frac{1}{P(O|\hat\lambda)}
P(O∣λ^)1 对于
Q
Q
Q 函数来说是个常数,不影响极值的求解,因此我们将其省去,得到:
Q
(
λ
∣
λ
^
)
=
∑
I
log
P
(
O
,
I
∣
λ
)
P
(
O
,
I
∣
λ
^
)
Q(\lambda|\hat\lambda)=\sum_I \log P(O,\,I|\lambda)P(O,\,I|\hat\lambda)
Q(λ∣λ^)=I∑logP(O,I∣λ)P(O,I∣λ^)
而:
P
(
O
,
I
∣
λ
)
=
π
i
1
b
i
1
(
o
1
)
a
i
1
i
2
⋯
a
i
T
−
1
i
T
b
i
T
(
o
T
)
P(O,\,I|\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}\cdots a_{i_{T-1}i_T}b_{i_T}(o_T)
P(O,I∣λ)=πi1bi1(o1)ai1i2⋯aiT−1iTbiT(oT)
因此
Q
Q
Q 函数可以写成:
Q
(
λ
∣
λ
^
)
=
∑
I
log
π
i
1
P
(
O
,
I
∣
λ
^
)
+
∑
I
(
∑
t
=
1
T
−
1
log
a
i
t
i
t
+
1
)
P
(
O
,
I
∣
λ
^
)
+
∑
I
(
∑
t
=
1
T
log
b
i
t
(
o
t
)
)
P
(
O
,
I
∣
λ
^
)
\begin{aligned} Q(\lambda|\hat\lambda) =&\, \sum_I\log\pi_{i_1}P(O,I|\hat\lambda) \\ +&\, \sum_I\left( \sum_{t=1}^{T-1} \log a_{i_ti_{t+1}} \right)P(O,I|\hat\lambda) \\ +&\, \sum_I\left( \sum_{t=1}^{T} \log b_{i_t}(o_t) \right)P(O,I|\hat\lambda) \end{aligned}
Q(λ∣λ^)=++I∑logπi1P(O,I∣λ^)I∑(t=1∑T−1logaitit+1)P(O,I∣λ^)I∑(t=1∑Tlogbit(ot))P(O,I∣λ^)
M 步
由于 π i \pi_i πi 、 a i j a_{ij} aij 和 b j ( k ) b_j(k) bj(k) 分别出现在 Q Q Q 函数的三项中,因此只需要对各项分别极大化:
- 求 π i \pi_i πi 极值点:可以进行一些变换,使用了类似于导出三硬币的 EM 算法时的技巧:
∑ I log π i 1 P ( O , I ∣ λ ^ ) = ∑ i 1 ∑ i t , t ≠ 1 log π i 1 P ( O , I ∣ λ ^ ) \begin{aligned} \sum_I\log\pi_{i_1}P(O,I|\hat\lambda) =&\, \sum_{i_1}\sum_{i_t,\,t\not=1}\log \pi_{i_1}P(O,I|\hat\lambda) \end{aligned} I∑logπi1P(O,I∣λ^)=i1∑it,t=1∑logπi1P(O,I∣λ^)
注意到在固定
i
1
i_1
i1 的取值时,有:
∑
i
t
,
t
≠
1
log
π
i
1
P
(
O
,
I
∣
λ
^
)
=
log
π
i
1
∑
i
t
,
t
≠
1
P
(
O
,
I
∣
λ
^
)
=
log
π
i
1
P
(
O
,
i
1
=
i
1
∣
λ
^
)
\sum_{i_t,\,t\not=1}\log \pi_{i_1}P(O,I|\hat\lambda)=\log \pi_{i_1}\sum_{i_t,\,t\not=1}P(O,I|\hat\lambda)=\log \pi_{i_1}P(O,i_1=i_1|\hat\lambda)
it,t=1∑logπi1P(O,I∣λ^)=logπi1it,t=1∑P(O,I∣λ^)=logπi1P(O,i1=i1∣λ^)
P
(
O
,
i
1
=
i
1
∣
λ
^
)
P(O,i_1=i_1|\hat\lambda)
P(O,i1=i1∣λ^) 这个记号写得不好。。。其实就是代表给定参数
λ
^
\hat\lambda
λ^ 的情况下,得到观测
O
O
O 并且第一个状态正好是刚刚固定的
i
1
i_1
i1 的概率。因此:
∑
I
log
π
i
1
P
(
O
,
I
∣
λ
^
)
=
∑
i
=
1
N
log
π
i
P
(
O
,
i
1
=
q
i
∣
λ
^
)
\sum_I\log\pi_{i_1}P(O,I|\hat\lambda)=\sum_{i=1}^{N}\log\pi_{i}P(O,i_1=q_i|\hat\lambda)
I∑logπi1P(O,I∣λ^)=i=1∑NlogπiP(O,i1=qi∣λ^)
这里
π
i
\pi_i
πi 满足约束条件
∑
i
=
1
N
π
i
=
1
\sum\limits_{i=1}^{N}\pi_i=1
i=1∑Nπi=1 ,使用 Lagrange 乘子法,Lagrangian 为:
L
(
π
)
=
∑
i
=
1
N
log
π
i
P
(
O
,
i
1
=
q
i
∣
λ
^
)
−
γ
(
1
−
∑
i
=
1
N
π
i
)
L(\pi)=\sum_{i=1}^{N}\log\pi_{i}P(O,i_1=q_i|\hat\lambda)-\gamma(1-\sum\limits_{i=1}^{N}\pi_i)
L(π)=i=1∑NlogπiP(O,i1=qi∣λ^)−γ(1−i=1∑Nπi)
FOC 为:
∂
L
(
π
)
∂
π
i
=
P
(
O
,
i
1
=
q
i
∣
λ
^
)
π
i
+
γ
=
0
⇒
P
(
O
,
i
1
=
q
i
∣
λ
^
)
+
π
i
γ
=
0
\begin{aligned} \frac{\partial L(\pi)}{\partial \pi_i} =&\,\frac{P(O,i_1=q_i|\hat\lambda)}{\pi_i}+\gamma=0 \\ \Rightarrow&\, P(O,i_1=q_i|\hat\lambda)+\pi_i\gamma=0 \end{aligned}
∂πi∂L(π)=⇒πiP(O,i1=qi∣λ^)+γ=0P(O,i1=qi∣λ^)+πiγ=0
对所有 FOC 求和,解得
γ
\gamma
γ 为:
γ
=
−
∑
i
=
1
N
P
(
O
,
i
1
=
q
i
∣
λ
^
)
=
−
P
(
O
∣
λ
^
)
\gamma=-\sum_{i=1}^{N}P(O,i_1=q_i|\hat\lambda)=-P(O|\hat\lambda)
γ=−i=1∑NP(O,i1=qi∣λ^)=−P(O∣λ^)
代回解得:
π
i
=
P
(
O
,
i
1
=
q
i
∣
λ
^
)
P
(
O
∣
λ
^
)
\pi_i=\frac{P(O,i_1=q_i|\hat\lambda)}{P(O|\hat\lambda)}
πi=P(O∣λ^)P(O,i1=qi∣λ^)
这实际上就是给定参数
λ
^
\hat\lambda
λ^ 和观测
O
O
O ,1 时刻经过状态
q
i
q_i
qi 的概率。
- 求 a i j a_{ij} aij 极值点:同样地,对目标函数进行一些变换:
∑ I ( ∑ t = 1 T − 1 log a i t i t + 1 ) P ( O , I ∣ λ ^ ) = ∑ I ∑ t = 1 T − 1 log a i t i t + 1 P ( O , I ∣ λ ^ ) (因为 P ( O , I ∣ λ ^ ) 与 t 无关) = ∑ t = 1 T − 1 ∑ I log a i t i t + 1 P ( O , I ∣ λ ^ ) (可以交换求和顺序) = ∑ t = 1 T − 1 ∑ i t ∑ i t + 1 ∑ i else log a i t i t + 1 P ( O , I ∣ λ ^ ) = ∑ t = 1 T − 1 ∑ i t ∑ i t + 1 log a i t i t + 1 ∑ i else P ( O , I ∣ λ ^ ) (因为 log a i t i t + 1 与 i else 无关) = ∑ t = 1 T − 1 ∑ i = 1 N ∑ j = 1 N log a i j P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) = ∑ i = 1 N ∑ j = 1 N ∑ t = 1 T − 1 log a i j P ( O , i t = q i , i t + 1 = q j ∣ λ ^ ) (可以交换求和顺序) \begin{aligned} &\, \sum_I\left( \sum_{t=1}^{T-1} \log a_{i_ti_{t+1}} \right)P(O,I|\hat\lambda) \\ =&\, \sum_I \sum_{t=1}^{T-1} \log a_{i_ti_{t+1}} P(O,I|\hat\lambda) \quad\text{(因为$P(O,I|\hat\lambda)$与$t$无关)} \\ =&\, \sum_{t=1}^{T-1}\sum_I \log a_{i_ti_{t+1}} P(O,I|\hat\lambda) \quad\text{(可以交换求和顺序)} \\ =&\, \sum_{t=1}^{T-1}\sum_{i_t}\sum_{i_{t+1}}\sum_{i_\text{else}}\log a_{i_ti_{t+1}} P(O,I|\hat\lambda) \\ =&\, \sum_{t=1}^{T-1}\sum_{i_t}\sum_{i_{t+1}}\log a_{i_ti_{t+1}}\sum_{i_\text{else}} P(O,I|\hat\lambda) \quad\text{(因为$\log a_{i_ti_{t+1}}$与$i_\text{else}$无关)} \\ =&\, \sum_{t=1}^{T-1}\sum_{i=1}^{N}\sum_{j=1}^{N}\log a_{ij} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda) \\ =&\, \sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{t=1}^{T-1}\log a_{ij} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda) \quad\text{(可以交换求和顺序)} \\ \end{aligned} ======I∑(t=1∑T−1logaitit+1)P(O,I∣λ^)I∑t=1∑T−1logaitit+1P(O,I∣λ^)(因为P(O,I∣λ^)与t无关)t=1∑T−1I∑logaitit+1P(O,I∣λ^)(可以交换求和顺序)t=1∑T−1it∑it+1∑ielse∑logaitit+1P(O,I∣λ^)t=1∑T−1it∑it+1∑logaitit+1ielse∑P(O,I∣λ^)(因为logaitit+1与ielse无关)t=1∑T−1i=1∑Nj=1∑NlogaijP(O,it=qi,it+1=qj∣λ^)i=1∑Nj=1∑Nt=1∑T−1logaijP(O,it=qi,it+1=qj∣λ^)(可以交换求和顺序)
约束条件同样是
∑
j
=
1
N
a
i
j
=
1
\sum\limits_{j=1}^{N}a_{ij}=1
j=1∑Naij=1 ,Lagrangian 为:
L
(
a
)
=
∑
i
=
1
N
∑
j
=
1
N
∑
t
=
1
T
−
1
log
a
i
j
P
(
O
,
i
t
=
q
i
,
i
t
+
1
=
q
j
∣
λ
^
)
−
∑
i
=
1
N
γ
i
(
1
−
∑
j
=
1
N
a
i
j
)
L(a)=\sum_{i=1}^{N}\sum_{j=1}^{N}\sum_{t=1}^{T-1}\log a_{ij} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)-\sum\limits_{i=1}^{N}\gamma_i(1-\sum\limits_{j=1}^{N}a_{ij})
L(a)=i=1∑Nj=1∑Nt=1∑T−1logaijP(O,it=qi,it+1=qj∣λ^)−i=1∑Nγi(1−j=1∑Naij)
FOC 为:
∂
L
(
a
)
∂
a
i
j
=
∑
t
=
1
T
−
1
P
(
O
,
i
t
=
q
i
,
i
t
+
1
=
q
j
∣
λ
^
)
a
i
j
+
γ
i
=
0
⇒
∑
t
=
1
T
−
1
P
(
O
,
i
t
=
q
i
,
i
t
+
1
=
q
j
∣
λ
^
)
+
a
i
j
γ
i
=
0
\begin{aligned} \frac{\partial L(a)}{\partial a_{ij}} =&\, \frac{\sum\limits_{t=1}^{T-1} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)}{a_{ij}}+\gamma_i=0 \\ \Rightarrow &\, \sum\limits_{t=1}^{T-1} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)+a_{ij}\gamma_i=0 \end{aligned}
∂aij∂L(a)=⇒aijt=1∑T−1P(O,it=qi,it+1=qj∣λ^)+γi=0t=1∑T−1P(O,it=qi,it+1=qj∣λ^)+aijγi=0
将所有
i
i
i 相同的 FOC 相加,得到:
γ
i
=
−
∑
t
=
1
T
−
1
P
(
O
,
i
t
=
q
i
∣
λ
^
)
\gamma_i=-\sum\limits_{t=1}^{T-1}P(O,i_t=q_i|\hat\lambda)
γi=−t=1∑T−1P(O,it=qi∣λ^)
代回解得:
a
i
j
=
∑
t
=
1
T
−
1
P
(
O
,
i
t
=
q
i
,
i
t
+
1
=
q
j
∣
λ
^
)
∑
t
=
1
T
−
1
P
(
O
,
i
t
=
q
i
∣
λ
^
)
a_{ij}=\frac{\sum\limits_{t=1}^{T-1} P(O,i_t=q_i,i_{t+1}=q_{j}|\hat\lambda)}{\sum\limits_{t=1}^{T-1}P(O,i_t=q_i|\hat\lambda)}
aij=t=1∑T−1P(O,it=qi∣λ^)t=1∑T−1P(O,it=qi,it+1=qj∣λ^)
- 求 b j ( k ) b_{j}(k) bj(k) 极值点:同样地,对目标函数进行一些变换:
∑ I ( ∑ t = 1 T log b i t ( o t ) ) P ( O , I ∣ λ ^ ) = ∑ I ∑ t = 1 T log b i t ( o t ) P ( O , I ∣ λ ^ ) (因为 P ( O , I ∣ λ ^ ) 与 t 无关) = ∑ t = 1 T ∑ I log b i t ( o t ) P ( O , I ∣ λ ^ ) (可以交换求和顺序) = ∑ t = 1 T ∑ i t ∑ i else log b i t ( o t ) P ( O , I ∣ λ ^ ) = ∑ t = 1 T ∑ i t log b i t ( o t ) ∑ i else P ( O , I ∣ λ ^ ) (因为 log b i t ( o t ) 与 i else 无关) = ∑ t = 1 T ∑ j = 1 N log b j ( o t ) P ( O , i t = q j ∣ λ ^ ) = ∑ j = 1 N ∑ t = 1 T log b j ( o t ) P ( O , i t = q j ∣ λ ^ ) \begin{aligned} &\, \sum_I\left( \sum_{t=1}^{T} \log b_{i_t}(o_t) \right)P(O,I|\hat\lambda) \\ =&\, \sum_I \sum_{t=1}^{T} \log b_{i_t}(o_t)P(O,I|\hat\lambda)\quad\text{(因为$P(O,I|\hat\lambda)$与$t$无关)} \\ =&\, \sum_{t=1}^{T}\sum_I \log b_{i_t}(o_t)P(O,I|\hat\lambda)\quad\text{(可以交换求和顺序)} \\ =&\, \sum_{t=1}^{T}\sum_{i_t}\sum_{i_\text{else}}\log b_{i_t}(o_t)P(O,I|\hat\lambda) \\ =&\, \sum_{t=1}^{T}\sum_{i_t}\log b_{i_t}(o_t)\sum_{i_\text{else}}P(O,I|\hat\lambda)\quad\text{(因为$\log b_{i_t}(o_t)$与$i_\text{else}$无关)} \\ =&\, \sum_{t=1}^{T}\sum\limits_{j=1}^{N}\log b_j(o_t)P(O,i_t=q_j|\hat\lambda) \\ =&\, \sum\limits_{j=1}^{N}\sum_{t=1}^{T}\log b_j(o_t)P(O,i_t=q_j|\hat\lambda) \end{aligned} ======I∑(t=1∑Tlogbit(ot))P(O,I∣λ^)I∑t=1∑Tlogbit(ot)P(O,I∣λ^)(因为P(O,I∣λ^)与t无关)t=1∑TI∑logbit(ot)P(O,I∣λ^)(可以交换求和顺序)t=1∑Tit∑ielse∑logbit(ot)P(O,I∣λ^)t=1∑Tit∑logbit(ot)ielse∑P(O,I∣λ^)(因为logbit(ot)与ielse无关)t=1∑Tj=1∑Nlogbj(ot)P(O,it=qj∣λ^)j=1∑Nt=1∑Tlogbj(ot)P(O,it=qj∣λ^)
约束条件为
∑
k
=
1
M
b
i
(
k
)
=
1
\sum\limits_{k=1}^{M}b_{i}(k)=1
k=1∑Mbi(k)=1 ,Lagrangian 为:
L
(
b
)
=
∑
j
=
1
N
∑
t
=
1
T
log
b
j
(
o
t
)
P
(
O
,
i
t
=
q
j
∣
λ
^
)
−
∑
j
=
1
N
γ
j
(
1
−
∑
k
=
1
M
b
i
(
k
)
)
L(b)=\sum\limits_{j=1}^{N}\sum_{t=1}^{T}\log b_j(o_t)P(O,i_t=q_j|\hat\lambda)-\sum_{j=1}^{N}\gamma_j(1-\sum\limits_{k=1}^{M}b_{i}(k))
L(b)=j=1∑Nt=1∑Tlogbj(ot)P(O,it=qj∣λ^)−j=1∑Nγj(1−k=1∑Mbi(k))
FOC 为(注意,只有
o
t
=
v
k
o_t=v_k
ot=vk 时
b
j
(
o
t
)
b_j(o_t)
bj(ot) 对
b
j
(
k
)
b_j(k)
bj(k) 的偏导数才不为 0,这里用指示函数来表示):
∂
L
(
b
)
∂
b
j
(
k
)
=
∑
t
=
1
T
P
(
O
,
i
t
=
q
j
∣
λ
^
)
I
(
o
t
=
v
k
)
b
j
(
k
)
+
γ
j
=
0
⇒
∑
t
=
1
T
P
(
O
,
i
t
=
q
j
∣
λ
^
)
I
(
o
t
=
v
k
)
+
b
j
(
k
)
γ
j
=
0
\begin{aligned} \frac{\partial L(b)}{\partial b_{j}(k)} =&\, \frac{\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)I(o_t=v_k)}{b_{j}(k)}+\gamma_j=0 \\ \Rightarrow &\, \sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)I(o_t=v_k)+b_{j}(k)\gamma_j=0 \end{aligned}
∂bj(k)∂L(b)=⇒bj(k)t=1∑TP(O,it=qj∣λ^)I(ot=vk)+γj=0t=1∑TP(O,it=qj∣λ^)I(ot=vk)+bj(k)γj=0
将所有
j
j
j 相同的 FOC 相加,得到(因为有且仅有一个
k
k
k 使得
I
(
o
t
=
v
k
)
=
1
I(o_t=v_k)=1
I(ot=vk)=1):
γ
j
=
−
∑
t
=
1
T
P
(
O
,
i
t
=
q
j
∣
λ
^
)
\gamma_j=-\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)
γj=−t=1∑TP(O,it=qj∣λ^)
代回解得:
b
j
(
k
)
=
∑
t
=
1
T
P
(
O
,
i
t
=
q
j
∣
λ
^
)
I
(
o
t
=
v
k
)
∑
t
=
1
T
P
(
O
,
i
t
=
q
j
∣
λ
^
)
b_j(k)=\frac{\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)I(o_t=v_k)}{\sum\limits_{t=1}^{T} P(O,i_t=q_{j}|\hat\lambda)}
bj(k)=t=1∑TP(O,it=qj∣λ^)t=1∑TP(O,it=qj∣λ^)I(ot=vk)
参数估计公式
以上参数估计的公式可以使用前向概率和后向概率表示,即:
a
i
j
=
∑
t
=
1
T
−
1
ξ
t
(
i
,
j
)
∑
t
=
1
T
−
1
γ
t
(
i
)
,
b
j
(
k
)
=
∑
t
=
1
,
o
t
=
v
k
T
γ
t
(
i
)
∑
t
=
1
T
γ
t
(
i
)
,
π
i
=
γ
1
(
i
)
a_{ij}=\frac{\sum\limits_{t=1}^{T-1}\xi_{t}(i,j)}{\sum\limits_{t=1}^{T-1}\gamma_t(i)} ,\quad\quad b_j(k)=\frac{\sum\limits_{t=1,o_t=v_k}^{T}\gamma_t(i)}{\sum\limits_{t=1}^{T}\gamma_t(i)} ,\quad\quad \pi_i=\gamma_1(i)
aij=t=1∑T−1γt(i)t=1∑T−1ξt(i,j),bj(k)=t=1∑Tγt(i)t=1,ot=vk∑Tγt(i),πi=γ1(i)
算法描述
输入:观测数据 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,\,o_2,\,\cdots,\,o_T) O=(o1,o2,⋯,oT) ;
输出:HMM 参数
- 初始化,对 n = 0 n=0 n=0 ,选取模型参数初始值 a i j ( 0 ) a_{ij}^{(0)} aij(0) , b j ( k ) ( 0 ) b_{j}(k)^{(0)} bj(k)(0) , π i ( 0 ) \pi_i^{(0)} πi(0) ;
- 递推,对于 n = 1 , 2 , ⋯ n=1,\,2,\,\cdots n=1,2,⋯ ,使用前一次递推得到的参数计算前向概率和后向概率,并更新参数:
a i j = ∑ t = 1 T − 1 ξ t ( i , j ) ∑ t = 1 T − 1 γ t ( i ) , b j ( k ) = ∑ t = 1 , o t = v k T γ t ( i ) ∑ t = 1 T γ t ( i ) , π i = γ 1 ( i ) a_{ij}=\frac{\sum\limits_{t=1}^{T-1}\xi_{t}(i,j)}{\sum\limits_{t=1}^{T-1}\gamma_t(i)} ,\quad\quad b_j(k)=\frac{\sum\limits_{t=1,o_t=v_k}^{T}\gamma_t(i)}{\sum\limits_{t=1}^{T}\gamma_t(i)} ,\quad\quad \pi_i=\gamma_1(i) aij=t=1∑T−1γt(i)t=1∑T−1ξt(i,j),bj(k)=t=1∑Tγt(i)t=1,ot=vk∑Tγt(i),πi=γ1(i)
- 中止,得到模型参数 λ ( n + 1 ) = ( A ( n + 1 ) , B ( n + 1 ) , π ( n + 1 ) ) \lambda^{(n+1)}=(A^{(n+1)},\,B^{(n+1)},\,\pi^{(n+1)}) λ(n+1)=(A(n+1),B(n+1),π(n+1)) ;
解码问题
解码问题是指,已知模型参数,给定观测序列,求出最有可能的对应的状态序列。
近似算法
回忆一下前面 γ t ( i ) \gamma_{t}(i) γt(i) 的定义是:给定模型 λ \lambda λ 和观测序列 O O O ,在时刻 t t t 处于状态 q i q_i qi 的概率。
近似算法是直接使用每一个时刻出现概率最大的状态作为输出,即:
i
t
∗
=
arg
max
1
≤
i
≤
N
[
γ
t
(
i
)
]
,
t
=
1
,
2
,
⋯
,
T
i_t^\ast=\arg \max_{1\leq i\leq N}[\gamma_t(i)],\quad t=1,2,\cdots,T
it∗=arg1≤i≤Nmax[γt(i)],t=1,2,⋯,T
从而得到状态序列
I
∗
=
(
i
1
∗
,
i
2
∗
,
⋯
,
i
T
∗
)
I^\ast=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast)
I∗=(i1∗,i2∗,⋯,iT∗) 。
近似算法顾名思义,就是近似的,没有更多地考虑到状态转移概率 a i j a_{ij} aij ,但是它计算简单。
Viterbi 算法
维特比算法实际上是动态规划,属于精确算法。原理为:最优路径的子路径一定是最优的(这里的最优指的是概率最大)。例如,若最优路径在 t t t 时刻经过节点 i t ∗ i_t^\ast it∗ ,则从 i t ∗ i_t^\ast it∗ 到 i T ∗ i_T^\ast iT∗ 的子路径一定是所有从 i t ∗ i_t^\ast it∗ 到 i T ∗ i_T^\ast iT∗ 的路径中最优的。否则我们可以选择更优的从 i t ∗ i_t^\ast it∗ 到 i T ∗ i_T^\ast iT∗ 的路径去替换原来的子路径,得到更优的总的路径。因此,我们从 t = 1 t=1 t=1 开始,递推地计算时刻 t t t 状态为 i i i 的各部分路径的最大概率,直至时刻 t = T t=T t=T 。
我们定义变量
δ
\delta
δ ,代表时刻
t
t
t 状态为
i
i
i 的所有单个路径
(
i
1
,
i
2
,
⋯
,
i
t
)
(i_1,i_2,\cdots,i_t)
(i1,i2,⋯,it) 中概率的最大值:
δ
t
(
i
)
=
max
(
i
1
,
i
2
,
⋯
,
i
t
)
P
(
i
t
=
i
,
o
t
,
⋯
,
o
1
∣
λ
)
,
i
=
1
,
2
,
⋯
,
N
\delta_t(i)=\max_{(i_1,i_2,\cdots,i_t)} P(i_t=i,o_t,\,\cdots,o_1|\lambda),\quad i=1,2,\cdots,N
δt(i)=(i1,i2,⋯,it)maxP(it=i,ot,⋯,o1∣λ),i=1,2,⋯,N
假设一个共同的起始节点为
q
0
q_0
q0 ,其到每个状态的转移概率为每个状态对应的初始概率,即
a
0
i
=
π
i
a_{0i}=\pi_i
a0i=πi 。
假设我们前面已经计算了时刻 [ 0 , t ] [0,\,t] [0,t] ,得到了 0 0 0 时刻从 i 0 = q 0 i_0=q_0 i0=q0 节点出发, t t t 时刻到达各个节点的最优路径和对应的概率 δ t ( j ) \delta_{t}(j) δt(j) 。则计算 t + 1 t+1 t+1 时刻时,对于某个状态 q i q_i qi ,我们只需求得 j = arg max j δ t ( j ) a j i b j ( o t + 1 ) j=\arg\max\limits_j \delta_{t}(j)a_{ji}b_{j}(o_{t+1}) j=argjmaxδt(j)ajibj(ot+1) ,则说明 δ t + 1 ( i ) = δ t ( j ) a j i b j ( o t + 1 ) \delta_{t+1}(i)=\delta_{t}(j)a_{ji}b_{j}(o_{t+1}) δt+1(i)=δt(j)ajibj(ot+1) ,并且 0 0 0 时刻从 i 0 i_0 i0 节点出发, t + 1 t+1 t+1 时刻到达状态 q i q_i qi 的最优路径中,前一个节点的状态就是 q j q_j qj 。
相应的递推公式为:
δ
t
+
1
(
i
)
=
max
1
≤
j
≤
N
δ
t
(
j
)
a
j
i
b
j
(
o
t
+
1
)
,
i
=
1
,
2
,
⋯
,
N
;
t
=
1
,
2
,
⋯
,
T
−
1
\delta_{t+1}(i)=\max_{1\leq j\leq N}\delta_{t}(j)a_{ji}b_{j}(o_{t+1}), \quad i=1,2,\cdots,N;\quad t=1,2,\cdots,T-1
δt+1(i)=1≤j≤Nmaxδt(j)ajibj(ot+1),i=1,2,⋯,N;t=1,2,⋯,T−1
算法中需要记录这个
q
j
q_j
qj ,我们定义变量
Ψ
t
(
i
)
\Psi_t(i)
Ψt(i) ,代表时刻
t
t
t 状态为
q
i
q_i
qi 的所有单个路径
(
i
1
,
i
2
,
⋯
,
i
t
−
1
,
i
t
)
(i_1,i_2,\cdots,i_{t-1},i_t)
(i1,i2,⋯,it−1,it) 中概率最大的路径的第
t
−
1
t-1
t−1 个节点为:
Ψ
t
(
i
)
=
arg
max
1
≤
j
≤
N
δ
t
(
j
)
a
j
i
b
j
(
o
t
+
1
)
,
i
=
1
,
2
,
⋯
,
N
\Psi_{t}(i)=\arg\max_{1\leq j\leq N}\delta_{t}(j)a_{ji}b_{j}(o_{t+1}),\quad i=1,2,\cdots,N
Ψt(i)=arg1≤j≤Nmaxδt(j)ajibj(ot+1),i=1,2,⋯,N
(我觉得算法中计算的东西可以叫做最优前缀子路径)
最后,当计算完所有最优前缀子路径后,我们取 i = arg max i δ t ( i ) i=\arg\max\limits_i \delta_t(i) i=argimaxδt(i) ,则说明我们所要求的总的最优路径的最后一个节点的状态是 q i q_i qi ,此时只需按照所记录的前一个节点的状态递推回去,就能得到整个最优路径。
算法:维比特算法
- 输入:模型 λ = ( A , B , π ) \lambda=(A,\,B,\,\pi) λ=(A,B,π) 和观测 O = ( o 1 , o 2 , ⋯ , o T ) O=(o_1,\,o_2,\,\cdots,o_T) O=(o1,o2,⋯,oT) ;
- 输出:最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^\ast=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast) I∗=(i1∗,i2∗,⋯,iT∗) ;
- 初始化:
δ 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , ⋯ , N Ψ 1 ( i ) = 0 , i = 1 , 2 , ⋯ , N \begin{array}{c} \delta_1(i)=\pi_i b_i(o_1),\quad i=1,2,\cdots ,N \\ \Psi_1(i)=0, \quad i=1,2,\cdots,N \end{array} δ1(i)=πibi(o1),i=1,2,⋯,NΨ1(i)=0,i=1,2,⋯,N
- 递推,对于 t = 2 , 3 , ⋯ , T t=2,3,\cdots,T t=2,3,⋯,T :
δ t ( i ) = max 1 ≤ j ≤ N δ t − 1 ( j ) a j i b i ( o t ) , i = 1 , 2 , ⋯ , N Ψ t ( i ) = arg max 1 ≤ j ≤ N δ t − 1 ( j ) a j i b i ( o t ) , i = 1 , 2 , ⋯ , N \begin{array}{c} \delta_{t}(i)=\max\limits_{1\leq j\leq N}\delta_{t-1}(j)a_{ji}b_{i}(o_{t}), \quad i=1,2,\cdots,N \\ \Psi_{t}(i)=\arg\max_{1\leq j\leq N}\delta_{t-1}(j)a_{ji}b_{i}(o_{t}),\quad i=1,2,\cdots,N \end{array} δt(i)=1≤j≤Nmaxδt−1(j)ajibi(ot),i=1,2,⋯,NΨt(i)=argmax1≤j≤Nδt−1(j)ajibi(ot),i=1,2,⋯,N
注意,这里
Ψ
t
(
i
)
\Psi_t(i)
Ψt(i) 的表达式也可以写成以下形式,因为
b
i
(
o
t
)
b_i(o_t)
bi(ot) 对于第
t
−
1
t-1
t−1 层而言是个常数,乘不乘进去都可以,反正对大家来说都是一样的效果:
Ψ
t
(
i
)
=
arg
max
1
≤
j
≤
N
δ
t
−
1
(
j
)
a
j
i
,
i
=
1
,
2
,
⋯
,
N
\Psi_{t}(i)=\arg\max_{1\leq j\leq N}\delta_{t-1}(j)a_{ji},\quad i=1,2,\cdots,N
Ψt(i)=arg1≤j≤Nmaxδt−1(j)aji,i=1,2,⋯,N
- 中止:
P ∗ = max 1 ≤ i ≤ N δ T ( i ) i T ∗ = arg max 1 ≤ i ≤ N δ T ( i ) \begin{array}{c} P^\ast=\max\limits_{1\leq i\leq N}\delta_T(i) \\ i^\ast_T=\arg \max\limits_{1\leq i\leq N}\delta_T(i) \end{array} P∗=1≤i≤NmaxδT(i)iT∗=arg1≤i≤NmaxδT(i)
- 最优路径回溯:对于 t = T − 1 , T − 2 , ⋯ , 1 t=T-1,T-2,\cdots,1 t=T−1,T−2,⋯,1 :
i t ∗ = Ψ t + 1 ( i t + 1 ∗ ) i^\ast_t=\Psi_{t+1}(i_{t+1}^\ast) it∗=Ψt+1(it+1∗)
即得到最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , ⋯ , i T ∗ ) I^\ast=(i_1^\ast,i_2^\ast,\cdots,i_T^\ast) I∗=(i1∗,i2∗,⋯,iT∗) ;
例(盒子和球模型):状态集合为
Q
=
{
1
,
2
,
3
}
Q=\set{1,\,2,\,3}
Q={1,2,3},观测集合为
V
=
{
r
,
w
}
V=\set{r,\,w}
V={r,w} ,
A
=
[
0.5
0.2
0.3
0.3
0.5
0.2
0.2
0.3
0.5
]
B
=
[
0.5
0.5
0.4
0.6
0.7
0.3
]
π
=
[
0.2
0.4
0.4
]
A=\begin{bmatrix} 0.5 & 0.2 & 0.3\\ 0.3 & 0.5 & 0.2\\ 0.2 & 0.3 & 0.5\\ \end{bmatrix} \quad B=\begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6\\ 0.7 & 0.3\\ \end{bmatrix} \quad \pi=\begin{bmatrix} 0.2\\ 0.4\\ 0.4\\ \end{bmatrix}
A=
0.50.30.20.20.50.30.30.20.5
B=
0.50.40.70.50.60.3
π=
0.20.40.4
假设得到的观测序列为
O
=
(
r
,
w
,
r
)
O=(r,\,w,\,r)
O=(r,w,r) ,则计算过程为:
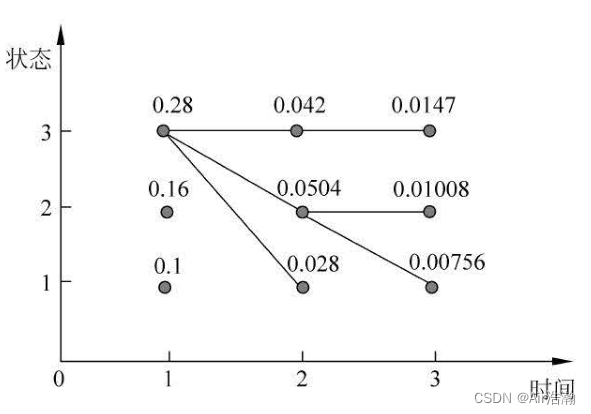
最优路径为 I ∗ = ( 3 , 3 , 3 ) I^\ast=(3,\,3,\,3) I∗=(3,3,3) ;