一、说明

        右退出是一项机器学习任务，其目标是根据一组特征向量预测真实值。存在多种回归算法：线性回归、逻辑回归、梯度提升或神经网络。在训练期间，这些算法中的每一个都会根据用于优化的损失函数来调整模型的权重。

        损失函数的选择取决于特定任务和需要实现的特定指标值。许多损失函数（如 MSE、MAE、RMSLE 等）专注于预测给定特征向量的变量的期望值。

        在本文中，我们将了解一种称为分位数损失的特殊损失函数，用于预测特定变量分位数。在深入研究分位数损失的细节之前，让我们简要回顾一下分位数这一术语。

二、分位数概念

分位数qₐ 是一个以 α * 100%的数字小于该值且(1 — α ) * 100%的数字大于该值的方式划分给定数字集的值。

α = 0.25、α = 0.5和α = 0.75的分位数qₐ经常在统计中使用，称为四分位数。这些四分位数分别表示为Q1、Q2和Q3。三个四分位数将数据分成 4 个相等的部分。

类似地，也存在将一组给定数字除以 100 个等份的百分位数p。百分位数表示为 pₐ，其中 α 是小于相应值的数字的百分比。

四分位数 Q1、Q2 和 Q3 分别对应于百分位数 p25、p50 和 p75。

        在下面的示例中，对于给定的一组数字，找到了所有三个四分位数。

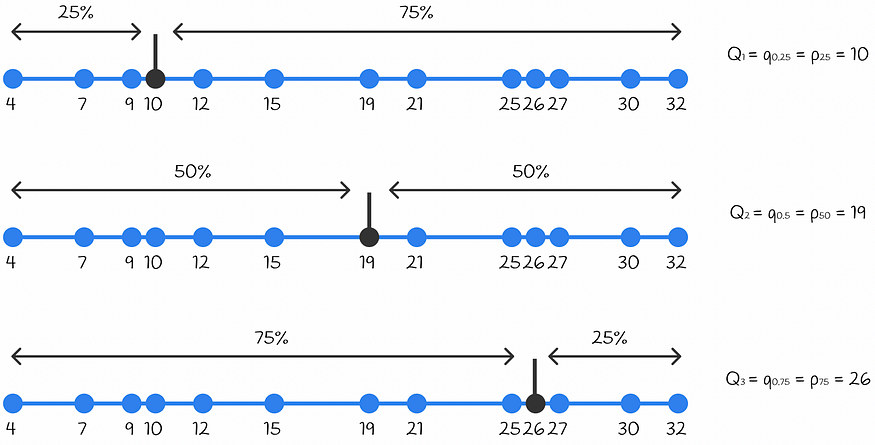
        显示给定数字集的所有三个四分位数的示例。第一个四分位数 Q1 等于 10，因为 25% 的值小于 10，75% 的值大于 10。以此类推到其他四分位数。

三、分位数损失函数

        旨在预测特定变量分位数的机器学习算法使用分位数损失作为损失函数。在讨论公式之前，让我们考虑一个简单的例子。

        想象一个问题，目标是预测变量的第 75 个百分位数。事实上，这一说法相当于预测误差在 75% 的情况下必须为负，而在另外 25% 的情况下必须为正。这就是分位数损失背后的实际直觉。

3.1 公式

分位数损失公式如下所示。α参数是指需要预测的分位数。

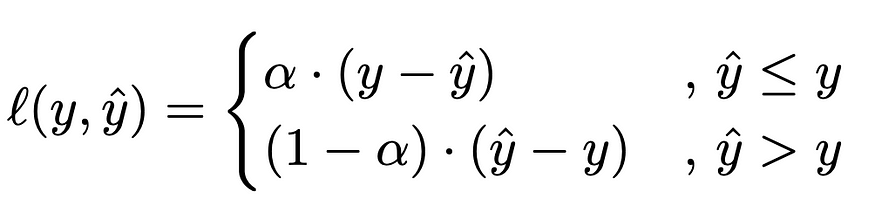
分位数损失公式

分位数损失的值取决于预测是小于还是大于真实值。为了更好地理解其背后的逻辑，我们假设我们的目标是预测第 80 个分位数，因此将α = 0.8的值代入方程中。结果，公式如下所示：

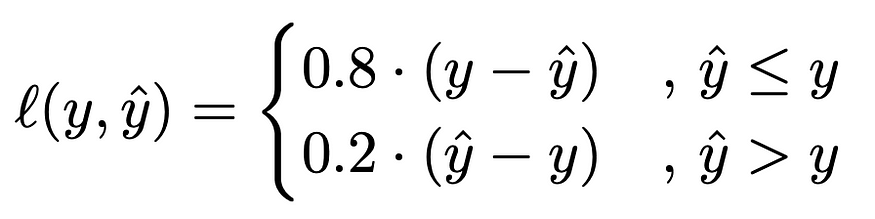
基本上，在这种情况下，分位数损失对低估预测的惩罚是高估预测的 4 倍。这样，模型对于低估的错误将更加关键，并且会更频繁地预测更高的值。因此，拟合模型平均在大约 80% 的情况下会高估结果，在 20% 的情况下会产生低估结果。

现在假设获得了对同一目标的两个预测。目标值为 40，而预测值为 30 和 50。让我们计算这两种情况下的分位数损失。尽管两种情况下的绝对误差 10 相同，但损失值不同：

• 对于 30，损失值为l = 0.8 * 10 = 8
• 对于 50，损失值为l = 0.2 * 10 = 2。

该损失函数如下图所示，显示了当真实值为 40 时α的不同参数的损失值。

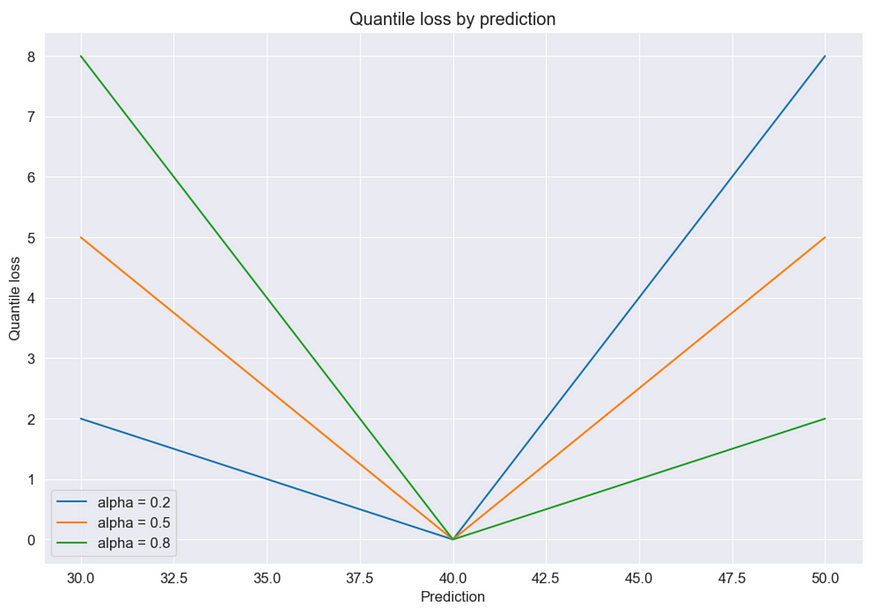
相反，如果α的值为 0.2，那么高估的预测将受到比低估的预测多 4 倍的惩罚。

预测某个变量分位数的问题称为分位数回归。

3.2 分位数损失例子

        让我们创建一个包含 10 000 个样本的综合数据集，其中视频游戏玩家的评分将根据玩游戏的小时数进行估计。

数据集生成

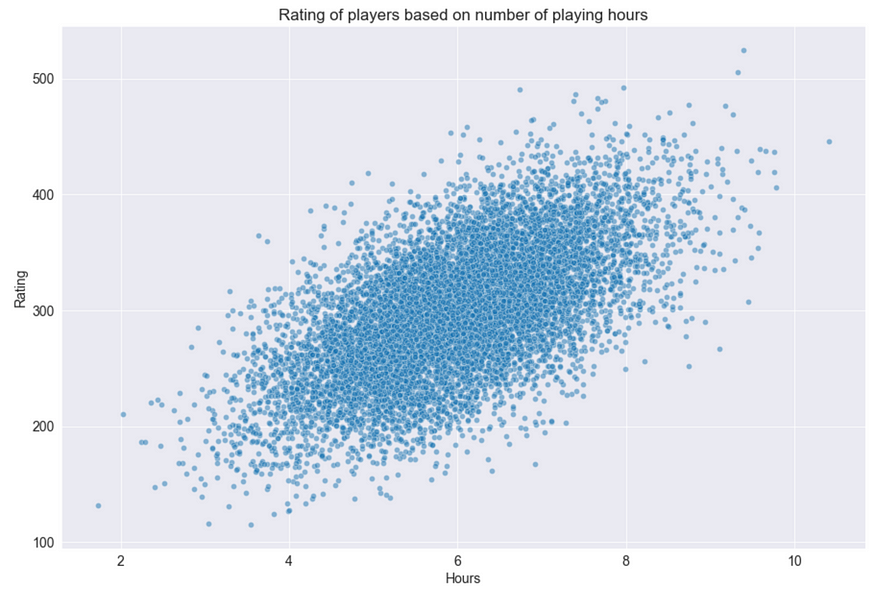
预测变量（小时）和目标（评级）之间的散点图

让我们按 80:20 的比例分割训练和测试的数据：

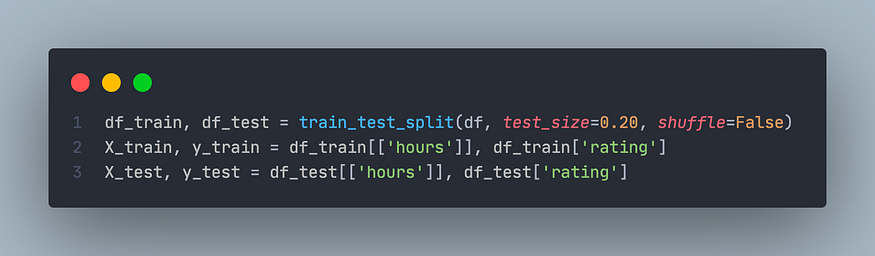
按 80:20 的比例分割数据集

        为了进行比较，我们建立 3 个具有不同α值的回归模型：0.2、0.5 和 0.8。每个回归模型都将由 LightGBM 创建，这是一个有效实现梯度提升的库。

        根据官方文档中的信息，LightGBM 允许通过将目标参数指定为'quantile'并传递相应的alpha值来解决分位数回归问题。

        训练 3 个模型后，它们可用于获得预测（第 6 行）。

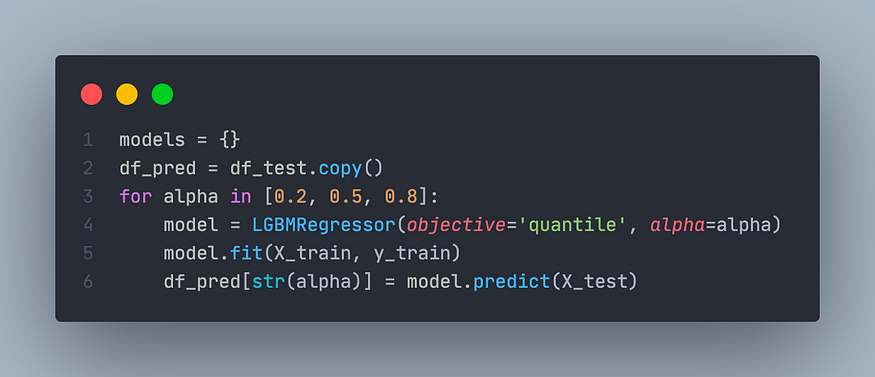
        使用目标 = '分位数' 训练 LGBM 模型

        让我们通过下面的代码片段可视化预测：

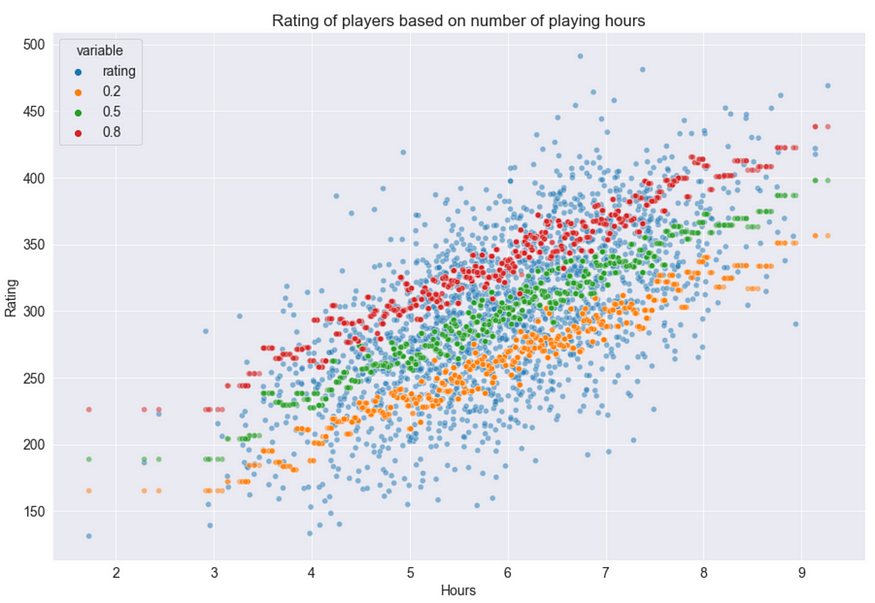
预测变量（小时）与真实/预测目标值之间的散点图

        从上面的散点图可以清楚地看出，α值越大，模型往往会生成更多高估的结果。此外，让我们将每个模型的预测与所有目标值进行比较。

不同模型的预测比较

        这将导致以下输出：

        输出的模式清晰可见：对于任何α ，在大约α * 100%的情况下，预测值都大于真实值。因此，我们可以通过实验得出结论，我们的预测模型工作正常。

分位数回归模型的预测误差在 α * 100%的情况下大约为负，在(1 — α ) * 100%的情况下为正。

四、结论

        我们发现了分位数损失——一种灵活的损失函数，可以合并到任何回归模型中来预测某个变量分位数。基于LightGBM的例子，我们看到了如何调整模型，从而解决分位数回归问题。事实上，许多其他流行的机器学习库允许将分位数损失设置为损失函数。