题目链接
Leetcode.4 寻找两个正序数组的中位数
hard
题目描述
给定两个大小分别为 m m m 和 n n n 的正序(从小到大)数组 n u m s 1 nums1 nums1 和 n u m s 2 nums2 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O ( l o g ( m + n ) ) O(log (m+n)) O(log(m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
- n u m s 1. l e n g t h = m nums1.length = m nums1.length=m
- n u m s 2. l e n g t h = n nums2.length = n nums2.length=n
- 0 ≤ m ≤ 1000 0 \leq m \leq 1000 0≤m≤1000
- 0 ≤ n ≤ 1000 0 \leq n \leq 1000 0≤n≤1000
- 1 ≤ m + n ≤ 2000 1 \leq m + n \leq 2000 1≤m+n≤2000
- − 1 0 6 ≤ n u m s 1 [ i ] , n u m s 2 [ i ] ≤ 1 0 6 -10^6 \leq nums1[i], nums2[i] \leq 10^6 −106≤nums1[i],nums2[i]≤106
解法:二分
我们设 n u m s 1 , n u m s 2 nums1 , nums2 nums1,nums2 的元素个数分别为 m , n m,n m,n。
由于我们是要找中位数,所以我们只需要找中间那个数,也就是第 ( m + n + 1 ) / 2 (m+n+1)/2 (m+n+1)/2个数。
我们令 k = ( m + n + 1 ) / 2 k = (m + n + 1) / 2 k=(m+n+1)/2。
由于 n u m s 1 , n u m s 2 nums1 , nums2 nums1,nums2 是排好序的,也就是我们要从这两个排好序的数组中,找出第 k k k 小的元素。
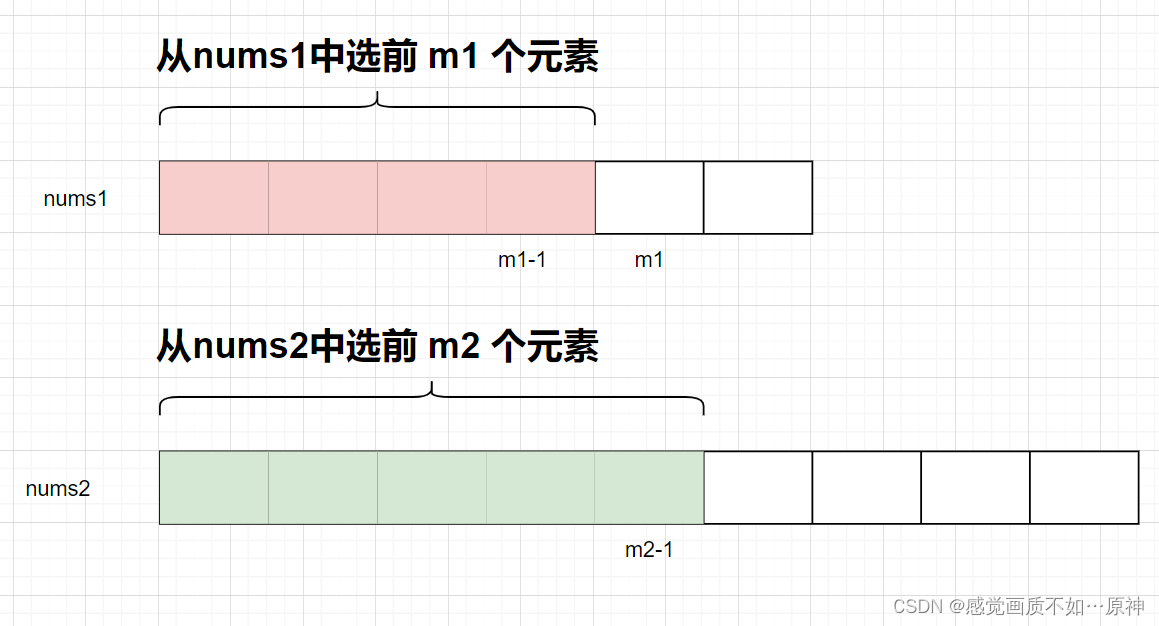
假设我们从 n u m s 1 nums1 nums1 中选出前 m 1 m_1 m1 个元素,那么就要从 n u m s 2 nums2 nums2 中选出前 m 2 = k − m 1 m_2 = k - m_1 m2=k−m1 个元素。
如果我们在 n u m s 1 nums1 nums1 中确定了前 m 1 m_1 m1 个元素,那么 m 2 m_2 m2 自然也确定了。
此时我们就可以使用二分,枚举从 n u m s 1 nums1 nums1 中选出元素个数 m 1 m_1 m1 。
初始时 l = 0 , r = m l = 0 , r = m l=0,r=m。
此时 m 1 m_1 m1 确定了 ,那么 m 2 = k − m 1 m_2 = k - m_1 m2=k−m1 自然也确定了,我们就进行如下判断:
1.如果 n u m s 1 [ m 1 ] < n u m s 2 [ m 2 − 1 ] nums1[m_1] < nums2[m_2-1] nums1[m1]<nums2[m2−1]。
那么在 n u m s 1 nums1 nums1 中比 n u m s 1 [ m 1 ] nums1[m_1] nums1[m1] 小的元素最多有 n u m s 1 [ 0 ] , n u m s 1 [ 1 ] , n u m s 1 [ 2 ] , . . . , n u m s 1 [ m 1 − 1 ] nums1[0],nums1[1],nums1[2],...,nums1[m_1-1] nums1[0],nums1[1],nums1[2],...,nums1[m1−1],一共有 m 1 m_1 m1 个。
那么在 n u m s 2 nums2 nums2 中比 n u m s 1 [ m 1 ] nums1[m_1] nums1[m1] 小的元素最多有 n u m s 2 [ 0 ] , n u m s 2 [ 1 ] , n u m s 2 [ 2 ] , . . . , n u m s 2 [ m 2 − 2 ] nums2[0],nums2[1],nums2[2],...,nums2[m_2-2] nums2[0],nums2[1],nums2[2],...,nums2[m2−2],一共有 m 2 − 1 m_2 - 1 m2−1 个。
所以一共有 m 1 + m 2 − 1 = k − 1 m_1 + m_2 - 1 = k - 1 m1+m2−1=k−1 个元素比 n u m s 1 [ m 1 ] nums1[m_1] nums1[m1] 小,所以左侧 n u m s 1 [ 0 ] , n u m s 1 [ 1 ] , n u m s 1 [ 2 ] , . . . , n u m s 1 [ m 1 − 1 ] nums1[0],nums1[1],nums1[2],...,nums1[m_1-1] nums1[0],nums1[1],nums1[2],...,nums1[m1−1] 都不可能是第 k k k 个元素,故 l = m 1 + 1 l = m_1 + 1 l=m1+1。
2.如果 n u m s 1 [ m 1 ] ≥ n u m s 2 [ m 2 − 1 ] nums1[m_1] \geq nums2[m_2-1] nums1[m1]≥nums2[m2−1]。
那么在 n u m s 1 nums1 nums1 中比 n u m s 1 [ m 1 ] nums1[m_1] nums1[m1] 小的元素最多有 n u m s 1 [ 0 ] , n u m s 1 [ 1 ] , n u m s 1 [ 2 ] , . . . , n u m s 1 [ m 1 − 1 ] nums1[0],nums1[1],nums1[2],...,nums1[m_1-1] nums1[0],nums1[1],nums1[2],...,nums1[m1−1],一共有 m 1 m_1 m1 个。
那么在 n u m s 2 nums2 nums2 中比 n u m s 1 [ m 1 ] nums1[m_1] nums1[m1] 小的元素最多有 n u m s 2 [ 0 ] , n u m s 2 [ 1 ] , n u m s 2 [ 2 ] , . . . , n u m s 2 [ m 2 − 2 ] , n u m s 2 [ m 2 − 1 ] nums2[0],nums2[1],nums2[2],...,nums2[m_2-2],nums2[m_2-1] nums2[0],nums2[1],nums2[2],...,nums2[m2−2],nums2[m2−1],一共有 m 2 m_2 m2 个。
所以一共有 m 1 + m 2 = k m_1 + m_2 = k m1+m2=k 个元素比 n u m s 1 [ m 1 ] nums1[m_1] nums1[m1] 小,所以当前 n u m s 1 [ m 1 − 1 ] nums1[m_1 - 1] nums1[m1−1],可以作为第 k k k 个元素,所以 r = m 1 r = m_1 r=m1。
时间复杂度: O ( l o g ( m + n ) ) O(log (m+n)) O(log(m+n))
C++代码:
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size() , n = nums2.size();
//我们枚举的一定是元素个数少的那个数组,否则会数组越界
if(m > n) return findMedianSortedArrays(nums2,nums1);
int k = (m + n + 1) / 2;
int l = 0 , r = m;
while(l < r){
int m1 = (l + r)>>1;
int m2 = k - m1;
if(nums1[m1] < nums2[m2 - 1]){
l = m1 + 1;
}
else r = m1;
}
int m1 = l , m2 = k - l;
//针对如下的特殊情况需要特判
/*
5 6 7
1 2 3 4
1 2 3
4 5 6 7
*/
int a = max(m1 <= 0 ? -1e9:nums1[m1 - 1],m2 <= 0 ? -1e9 : nums2[m2 - 1]);
if((m + n) & 1) return a;
int b = min(m1 >= m ? 1e9 : nums1[m1],m2 >= n ? 1e9 : nums2[m2]);
return (a + b) / 2.0;
}
};