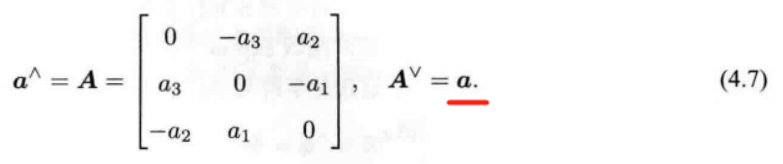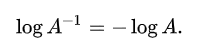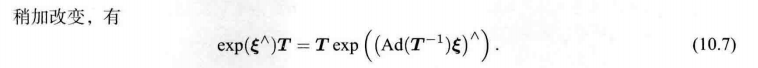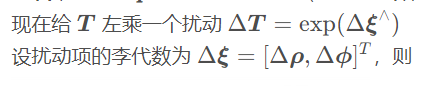文章目录
- 第10讲 后端2
- 10.1 滑动窗口滤波 和 优化
- 10.1.2 滑动窗口法
- 10.2 位姿图
- 10.3 实践: 位姿图优化
- 本讲 CMakeLists.txt
- 10.3.1 g2o 原生位姿图 【Code】
- 10.3.2 李代数上的位姿优化 【Code】
- 习题10
- 题1 【没推完】
- LaTex
第10讲 后端2
滑动窗口优化
位姿图优化【简化的BA】
带IMU 紧耦合 的优化
g2o 的位姿图
第9讲 以BA为主的图优化。
BA能精确地优化每个相机位姿与特征点位置。
在大场景中,大量特征点 会严重降低计算效率,计算量越来越大 ——> 无法实时化。
改进: 简化BA 【位姿图】
10.1 滑动窗口滤波 和 优化
BA:带有相机位姿和空间点的图优化。
控制 BA 规模:仅保留 离当前时刻最近的 N 个关键帧。【滑动窗口法】
ORB-SLAM2 :
共视图(Covisibility graph) : 与现在的相机 存在共同观测的关键帧构成的图。
10.1.2 滑动窗口法



滑动窗口法 比较适合VO系统,不适合大规模建图系统。
10.2 位姿图

10.3 实践: 位姿图优化
本讲 CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
project(pose_graph)
set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-std=c++17 -O2")
list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake_modules)
# Eigen
include_directories("/usr/include/eigen3")
# sophus
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
# g2o
find_package(G2O REQUIRED)
include_directories(${G2O_INCLUDE_DIRS})
add_executable(pose_graph_g2o_SE3 pose_graph_g2o_SE3.cpp)
target_link_libraries(pose_graph_g2o_SE3
g2o_core g2o_stuff g2o_types_slam3d ${CHOLMOD_LIBRARIES}
)
SET(G2O_LIBS g2o_csparse_extension g2o_stuff g2o_core cxsparse)
add_executable(pose_graph_g2o_lie pose_graph_g2o_lie_algebra.cpp)
target_link_libraries(pose_graph_g2o_lie
${G2O_LIBS}
${CHOLMOD_LIBRARIES}
${Sophus_LIBRARIES})
——————————
改动1:
SE3d 和 SO3d 去掉d
改动2:
CMakeLists.txt 加这一句 使满足 C++17标准, 最新版 g2o 需要
改动3: CMakeLists.txt 添加 csparse 相关的链接库
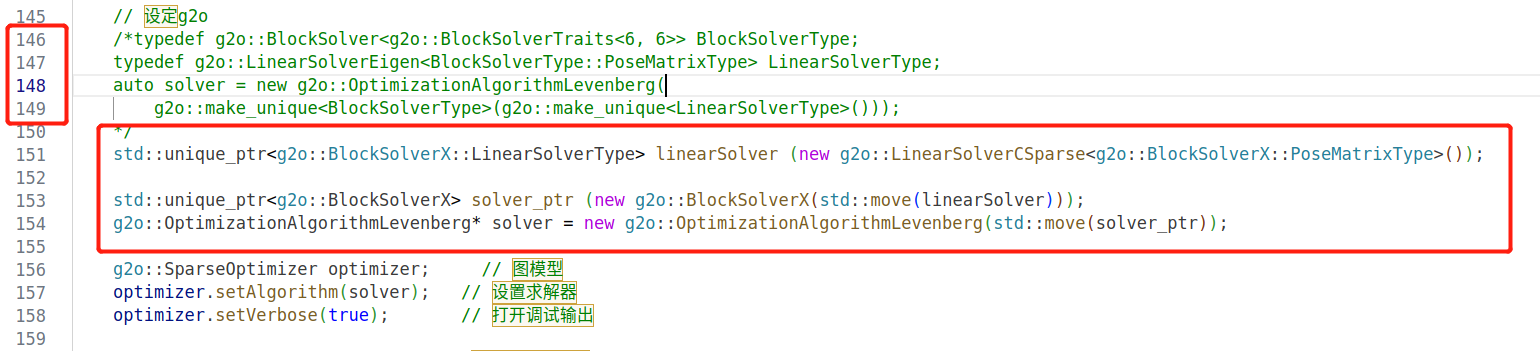
std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver (new g2o::LinearSolverEigen<g2o::BlockSolverX::PoseMatrixType>()); // 这里直接用 前面提到的Eigen 线性方程求解库 也可以
std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));
10.3.1 g2o 原生位姿图 【Code】
查看待优化的位姿图。注意在文件sphere.g2o所在文件夹打开命令行窗口。
g2o_viewer sphere.g2o

mkdir build && cd build
cmake ..
make
./pose_graph_g2o_SE3 ../sphere.g2o
g2o_viewer result.g2o


pose_graph_g2o_SE3.cpp
#include <iostream>
#include <fstream>
#include <string>
#include <g2o/types/slam3d/types_slam3d.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>
using namespace std;
/************************************************
* 本程序演示如何用g2o solver进行位姿图优化
* sphere.g2o是人工生成的一个Pose graph,我们来优化它。
* 尽管可以直接通过load函数读取整个图,但我们还是自己来实现读取代码,以期获得更深刻的理解
* 这里使用g2o/types/slam3d/中的SE3表示位姿,它实质上是四元数而非李代数.
* **********************************************/
int main(int argc, char **argv) {
if (argc != 2) {
cout << "Usage: pose_graph_g2o_SE3 sphere.g2o" << endl;
return 1;
}
ifstream fin(argv[1]);
if (!fin) {
cout << "file " << argv[1] << " does not exist." << endl;
return 1;
}
// 设定g2o
/*typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 6>> BlockSolverType;
typedef g2o::LinearSolverEigen<BlockSolverType::PoseMatrixType> LinearSolverType;
auto solver = new g2o::OptimizationAlgorithmLevenberg(
g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
*/
std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver (new g2o::LinearSolverEigen<g2o::BlockSolverX::PoseMatrixType>());
std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
int vertexCnt = 0, edgeCnt = 0; // 顶点和边的数量
while (!fin.eof()) {
string name;
fin >> name;
if (name == "VERTEX_SE3:QUAT") {
// SE3 顶点
g2o::VertexSE3 *v = new g2o::VertexSE3();
int index = 0;
fin >> index;
v->setId(index);
v->read(fin);
optimizer.addVertex(v);
vertexCnt++;
if (index == 0)
v->setFixed(true);
} else if (name == "EDGE_SE3:QUAT") {
// SE3-SE3 边
g2o::EdgeSE3 *e = new g2o::EdgeSE3();
int idx1, idx2; // 关联的两个顶点
fin >> idx1 >> idx2;
e->setId(edgeCnt++);
e->setVertex(0, optimizer.vertices()[idx1]);
e->setVertex(1, optimizer.vertices()[idx2]);
e->read(fin);
optimizer.addEdge(e);
}
if (!fin.good()) break;
}
cout << "read total " << vertexCnt << " vertices, " << edgeCnt << " edges." << endl;
cout << "optimizing ..." << endl;
optimizer.initializeOptimization();
optimizer.optimize(30);
cout << "saving optimization results ..." << endl;
optimizer.save("result.g2o");
return 0;
}
10.3.2 李代数上的位姿优化 【Code】
前端和后端 分开: 跟踪和建图
报错:
xixi@ubuntu:~/Downloads/slambook2-master/ch10/build$ ./pose_graph_g2o_lie ../sphere.g2o
Segmentation fault
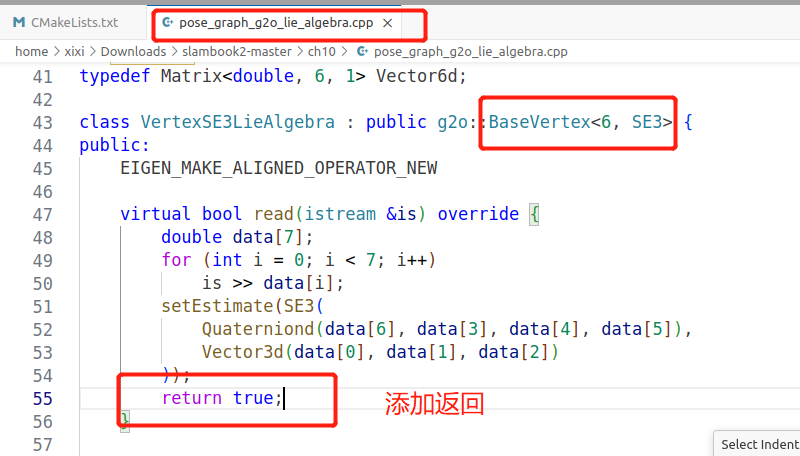
./pose_graph_g2o_lie ../sphere.g2o
g2o_viewer result.g2o

pose_graph_g2o_lie_algebra.cpp
#include <iostream>
#include <fstream>
#include <string>
#include <Eigen/Core>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_binary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>
#include <sophus/se3.h>
using namespace std;
using namespace Eigen;
using Sophus::SE3;
using Sophus::SO3;
/************************************************
* 本程序演示如何用g2o solver进行位姿图优化
* sphere.g2o是人工生成的一个Pose graph,我们来优化它。
* 尽管可以直接通过load函数读取整个图,但我们还是自己来实现读取代码,以期获得更深刻的理解
* 本节使用李代数表达位姿图,节点和边的方式为自定义
* **********************************************/
typedef Matrix<double, 6, 6> Matrix6d;
// 给定误差求J_R^{-1}的近似
Matrix6d JRInv(const SE3 &e) {
Matrix6d J;
J.block(0, 0, 3, 3) = SO3::hat(e.so3().log());
J.block(0, 3, 3, 3) = SO3::hat(e.translation());
J.block(3, 0, 3, 3) = Matrix3d::Zero(3, 3);
J.block(3, 3, 3, 3) = SO3::hat(e.so3().log());
// J = J * 0.5 + Matrix6d::Identity();
J = Matrix6d::Identity(); // try Identity if you want
return J;
}
// 李代数顶点
typedef Matrix<double, 6, 1> Vector6d;
class VertexSE3LieAlgebra : public g2o::BaseVertex<6, SE3> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
virtual bool read(istream &is) override {
double data[7];
for (int i = 0; i < 7; i++)
is >> data[i];
setEstimate(SE3(
Quaterniond(data[6], data[3], data[4], data[5]),
Vector3d(data[0], data[1], data[2])
));
return true;
}
virtual bool write(ostream &os) const override {
os << id() << " ";
Quaterniond q = _estimate.unit_quaternion();
os << _estimate.translation().transpose() << " ";
os << q.coeffs()[0] << " " << q.coeffs()[1] << " " << q.coeffs()[2] << " " << q.coeffs()[3] << endl;
return true;
}
virtual void setToOriginImpl() override {
_estimate = SE3();
}
// 左乘更新
virtual void oplusImpl(const double *update) override {
Vector6d upd;
upd << update[0], update[1], update[2], update[3], update[4], update[5];
_estimate = SE3::exp(upd) * _estimate;
}
};
// 两个李代数节点之边
class EdgeSE3LieAlgebra : public g2o::BaseBinaryEdge<6, SE3, VertexSE3LieAlgebra, VertexSE3LieAlgebra> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
virtual bool read(istream &is) override {
double data[7];
for (int i = 0; i < 7; i++)
is >> data[i];
Quaterniond q(data[6], data[3], data[4], data[5]);
q.normalize();
setMeasurement(SE3(q, Vector3d(data[0], data[1], data[2])));
for (int i = 0; i < information().rows() && is.good(); i++)
for (int j = i; j < information().cols() && is.good(); j++) {
is >> information()(i, j);
if (i != j)
information()(j, i) = information()(i, j);
}
return true;
}
virtual bool write(ostream &os) const override {
VertexSE3LieAlgebra *v1 = static_cast<VertexSE3LieAlgebra *> (_vertices[0]);
VertexSE3LieAlgebra *v2 = static_cast<VertexSE3LieAlgebra *> (_vertices[1]);
os << v1->id() << " " << v2->id() << " ";
SE3 m = _measurement;
Eigen::Quaterniond q = m.unit_quaternion();
os << m.translation().transpose() << " ";
os << q.coeffs()[0] << " " << q.coeffs()[1] << " " << q.coeffs()[2] << " " << q.coeffs()[3] << " ";
// information matrix
for (int i = 0; i < information().rows(); i++)
for (int j = i; j < information().cols(); j++) {
os << information()(i, j) << " ";
}
os << endl;
return true;
}
// 误差计算与书中推导一致
virtual void computeError() override {
SE3 v1 = (static_cast<VertexSE3LieAlgebra *> (_vertices[0]))->estimate();
SE3 v2 = (static_cast<VertexSE3LieAlgebra *> (_vertices[1]))->estimate();
_error = (_measurement.inverse() * v1.inverse() * v2).log();
}
// 雅可比计算
virtual void linearizeOplus() override {
SE3 v1 = (static_cast<VertexSE3LieAlgebra *> (_vertices[0]))->estimate();
SE3 v2 = (static_cast<VertexSE3LieAlgebra *> (_vertices[1]))->estimate();
Matrix6d J = JRInv(SE3::exp(_error));
// 尝试把J近似为I?
_jacobianOplusXi = -J * v2.inverse().Adj();
_jacobianOplusXj = J * v2.inverse().Adj();
}
};
int main(int argc, char **argv) {
if (argc != 2) {
cout << "Usage: pose_graph_g2o_SE3_lie sphere.g2o" << endl;
return 1;
}
ifstream fin(argv[1]);
if (!fin) {
cout << "file " << argv[1] << " does not exist." << endl;
return 1;
}
// 设定g2o
/*typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 6>> BlockSolverType;
typedef g2o::LinearSolverEigen<BlockSolverType::PoseMatrixType> LinearSolverType;
auto solver = new g2o::OptimizationAlgorithmLevenberg(
g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
*/
std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver (new g2o::LinearSolverEigen<g2o::BlockSolverX::PoseMatrixType>());
std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
int vertexCnt = 0, edgeCnt = 0; // 顶点和边的数量
vector<VertexSE3LieAlgebra *> vectices;
vector<EdgeSE3LieAlgebra *> edges;
while (!fin.eof()) {
string name;
fin >> name;
if (name == "VERTEX_SE3:QUAT") {
// 顶点
VertexSE3LieAlgebra *v = new VertexSE3LieAlgebra();
int index = 0;
fin >> index;
v->setId(index);
v->read(fin);
optimizer.addVertex(v);
vertexCnt++;
vectices.push_back(v);
if (index == 0)
v->setFixed(true);
} else if (name == "EDGE_SE3:QUAT") {
// SE3-SE3 边
EdgeSE3LieAlgebra *e = new EdgeSE3LieAlgebra();
int idx1, idx2; // 关联的两个顶点
fin >> idx1 >> idx2;
e->setId(edgeCnt++);
e->setVertex(0, optimizer.vertices()[idx1]);
e->setVertex(1, optimizer.vertices()[idx2]);
e->read(fin);
optimizer.addEdge(e);
edges.push_back(e);
}
if (!fin.good()) break;
}
cout << "read total " << vertexCnt << " vertices, " << edgeCnt << " edges." << endl;
cout << "optimizing ..." << endl;
optimizer.initializeOptimization();
optimizer.optimize(30);
cout << "saving optimization results ..." << endl;
// 因为用了自定义顶点且没有向g2o注册,这里保存自己来实现
// 伪装成 SE3 顶点和边,让 g2o_viewer 可以认出
ofstream fout("result_lie.g2o");
for (VertexSE3LieAlgebra *v:vectices) {
fout << "VERTEX_SE3:QUAT ";
v->write(fout);
}
for (EdgeSE3LieAlgebra *e:edges) {
fout << "EDGE_SE3:QUAT ";
e->write(fout);
}
fout.close();
return 0;
}
习题10

题1 【没推完】
如果将位姿图中的误差定义为 Δ ξ i j = ξ i ∘ ξ j − 1 \Delta \bm{\xi}_{ij}=\bm{\xi}_{i} \circ \bm{\xi}^{-1}_{j} Δξij=ξi∘ξj−1 ,推导按照此定义的左乘扰动雅克比矩阵。
本题中 位姿图的误差定义为 Δ ξ i j = ξ i ∘ ξ j − 1 = ln ( T i T j − 1 ) ∨ \Delta \bm{\xi}_{ij}=\bm{\xi}_{i} \circ \bm{\xi}^{-1}_{j}=\ln (\bm{T}_i\bm{T}_j^{-1})^{\vee} Δξij=ξi∘ξj−1=ln(TiTj−1)∨
- 和 P271 的定义区别在于 是第二个 求逆。这里是相对第 j j j 个位姿的坐标系进行位姿变化讨论
- T \bm{T} T 对应的李代数为 ξ \bm{\xi} ξ
对应的李群写法为: T j i = T i T j − 1 \bm{T}_{ji}=\bm{T}_i\bm{T}_j^{-1} Tji=TiTj−1
构建误差 e i j \bm{e}_{ij} eij
- 这样构建的误差理想下是0,因为 ln( I ) = 0 \bm{I})=\bm{0} I)=0。怎么感觉应该是下面这样的🤔
e
i
j
=
ln
(
T
j
i
−
1
T
i
T
j
−
1
)
∨
\bm{e}_{ij}=\ln (\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1})^{\vee}
eij=ln(Tji−1TiTj−1)∨
其中
T j i = T i T j − 1 \bm{T}_{ji}=\bm{T}_i\bm{T}_j^{-1} Tji=TiTj−1
T j i − 1 T j i = T j i − 1 T i T j − 1 \bm{T}_{ji}^{-1}\bm{T}_{ji}=\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1} Tji−1Tji=Tji−1TiTj−1
I = T j i − 1 T i T j − 1 \bm{I}=\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1} I=Tji−1TiTj−1
给 ξ i \bm{\xi}_i ξi 和 ξ j \bm{\xi}_j ξj 各一个左扰动
e ^ i j = ln ( T j i − 1 exp ( Δ ξ i ∧ ) T i ( exp ( Δ ξ j ∧ ) T j ) − 1 ) ∨ = ln ( T j i − 1 exp ( Δ ξ i ∧ ) T i T j − 1 ( exp ( Δ ξ j ∧ ) − 1 ) ∨ 由式 ( 10.7 ) = ln ( T j i − 1 T i exp ( ( A d ( T i − 1 ) Δ ξ i ) ∧ ) exp ( ( − A d ( T j − 1 ) Δ ξ j ) ∧ ) T j − 1 ) ∨ = l n ( T j i − 1 T i T j − 1 exp ( ( A d ( T i − 1 ) Δ ξ i ) ∧ ) exp ( ( − A d ( T j − 1 ) Δ ξ j ) ∧ ) ) ∨ = l n ( exp ( e i j ) exp ( ( A d ( T i − 1 ) Δ ξ i ) ∧ ) exp ( ( − A d ( T j − 1 ) Δ ξ j ) ∧ ) ) ∨ \begin{align*}\bm{\hat{e}}_{ij} &=\ln (\bm{T}_{ji}^{-1}\exp(\Delta \bm{\xi}_i^{\land})\bm{T}_i(\exp(\Delta \bm{\xi}_j^{\land})\bm{T}_j)^{-1})^{\vee} \\ &= \ln (\bm{T}_{ji}^{-1}\exp(\Delta \bm{\xi}_i^{\land})\bm{T}_i\bm{T}_j^{-1}(\exp(\Delta \bm{\xi}_j^{\land})^{-1})^{\vee} \\ & 由 式 (10.7) \\ &= \ln (\bm{T}_{ji}^{-1}\bm{T}_i\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land})\bm{T}_j^{-1})^{\vee} \\ &= \mathrm{ln}(\bm{T}_{ji}^{-1}\bm{T}_i\bm{T}_j^{-1}\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land}))^{\vee} \\ &= \mathrm{ln}(\exp(\bm{e}_{ij})\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land}))^{\vee} \\ \end{align*} e^ij=ln(Tji−1exp(Δξi∧)Ti(exp(Δξj∧)Tj)−1)∨=ln(Tji−1exp(Δξi∧)TiTj−1(exp(Δξj∧)−1)∨由式(10.7)=ln(Tji−1Tiexp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧)Tj−1)∨=ln(Tji−1TiTj−1exp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧))∨=ln(exp(eij)exp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧))∨
由公式:
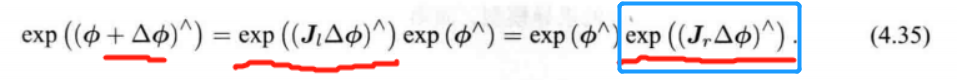
对于
T
i
\bm{T}_i
Ti
l
n
(
exp
(
e
i
j
)
exp
(
(
A
d
(
T
i
−
1
)
Δ
ξ
i
)
∧
)
exp
(
(
−
A
d
(
T
j
−
1
)
Δ
ξ
j
)
∧
)
)
∨
≈
\mathrm{ln}(\exp(\bm{e}_{ij})\exp((\mathrm{Ad}(\bm{T}_i^{-1})\Delta \bm{\xi}_i)^{\land})\exp((\mathrm{-Ad}(\bm{T}_j^{-1})\Delta \bm{\xi}_j)^{\land}))^{\vee} \approx
ln(exp(eij)exp((Ad(Ti−1)Δξi)∧)exp((−Ad(Tj−1)Δξj)∧))∨≈
LaTex
$\circ$
∘ \circ ∘