一、什么是二叉搜索树
二叉搜索树（BST，Binary Search Tree），也称二叉排序树或二叉查找树
二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质
非空左子树的所有键值小于其根结点的键值
非空右子树的所有键值大于其根结点的键值
左、右子树都是二叉搜索树

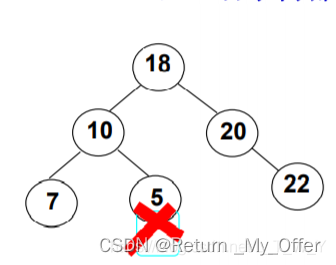
上图值为10的结点的右子树为7，比10小，不满足条件2，所以这棵树不是二叉搜索树

上图各个结点都满足条件，所以这棵树是二叉搜索树

上图各个结点都满足条件，所以这棵树也是二叉搜索树
看完上面的介绍后，相信大家都对什么是二叉搜索树有了较为清晰的认识。接下来说一下二叉搜索树的一些基本操作
给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和

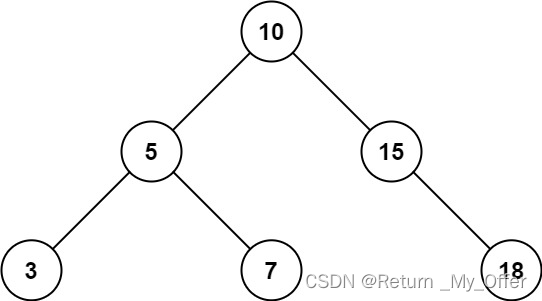
输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32


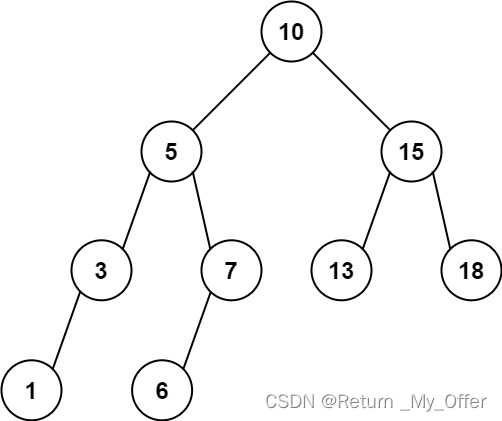
输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

方法：深度优先搜索

思路
按深度优先搜索的顺序计算范围和。记当前子树根节点为 root\textit{root}root，分以下四种情况讨论：
root 节点为空
返回 0
root 节点的值大于 high
由于二叉搜索树右子树上所有节点的值均大于根节点的值，即均大于 high，故无需考虑右子树，返回左子树的范围和
root 节点的值小于 low
由于二叉搜索树左子树上所有节点的值均小于根节点的值，即均小于low，故无需考虑左子树，返回右子树的范围和
root节点的值在[low,high] 范围内
此时应返回root 节点的值、左子树的范围和、右子树的范围和这三者之和

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


int rangeSumBST(struct TreeNode* root, int low, int high){
    if(root==NULL)
    {
        return 0;
    }
    if(root->val>high)
    {
        return rangeSumBST(root->left,low,high);
    }
    if(root->val<low)
    {
        return rangeSumBST(root->right,low,high);
    }
    return root->val+rangeSumBST(root->left, low, high)
    +rangeSumBST(root->right,  low,  high);
}