---

线性规划的发展被认为是20世纪中叶最重要的科学进步之一，从1950年起，线性规划就产生了非常大的影响。在计算机上进行的科学计算很大一部分都是线性规划的应用。

线性规划的本质是什么？线性规划能够解决什么类型的问题？

简单来说，线性规划中最普遍应用的问题类型是在竞争性活动中以最佳的方式分配有限资源的问题。例如：生产设施的分配、国家资源的分配、海运模式的选择、农业生产计划等。

线性规划使用数学模型描述相关问题。“线性”意味着模型中所有数学函数都是线性函数。“规划”指的不是计算机程序，它实质上是“计划”的同义词。因此，线性规划涉及获得最优结果的活动计划，如达到一个在所有可行方案中最好的特定目标（根据数学模型）。

数学模型符合线性规划一般形式的任何问题都是线性规划问题，因此，线性规划问题和它们的模型是可交换的，简称为线性规划，或直接写为LP。

此外，被称为单纯形法的一个非常有效的方法，可以用来求解大规模的线性规划问题，这也是线性规划产生巨大影响的原因。

一、原形范例（Wyndor Glass 公司）

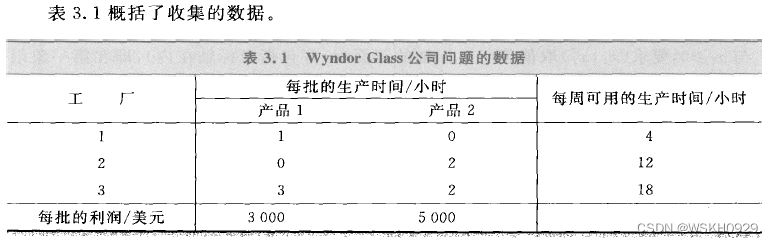
这是一个典型的生产组合型的线性规划问题。

1.1 线性规划模型构建

1.2 图解法

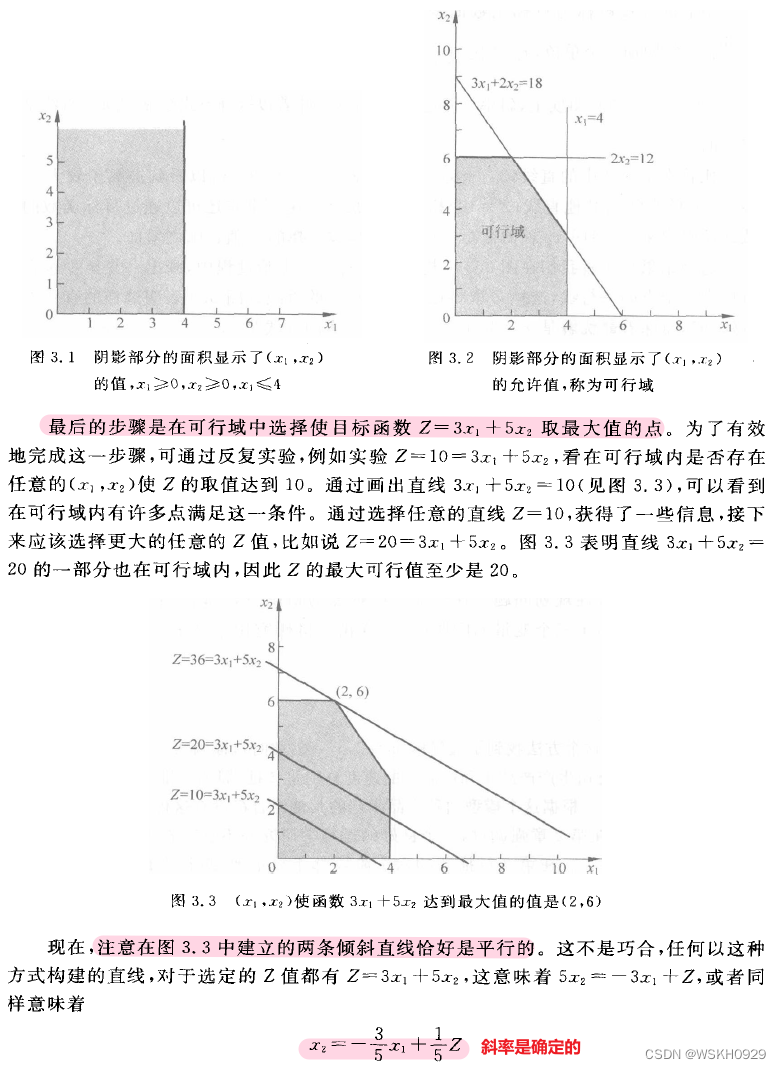
1.3 结论

二、线性规划模型

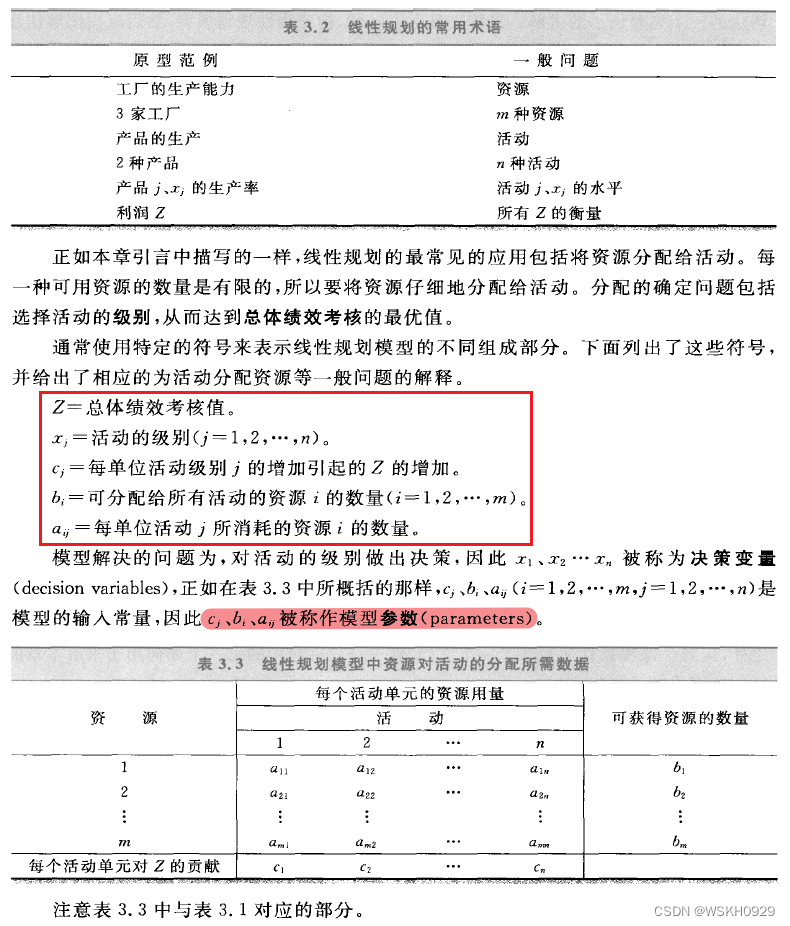
2.1 线性规划模型的标准形式

2.2 其他形式

2.3 模型解的术语

• 解：决策变量的任何特定值组合都被称为一个解
• 可行解：满足所有约束条件的解
• 非可行解：至少有一个约束条件不满足的解
• 可行域：所有可行解的集合

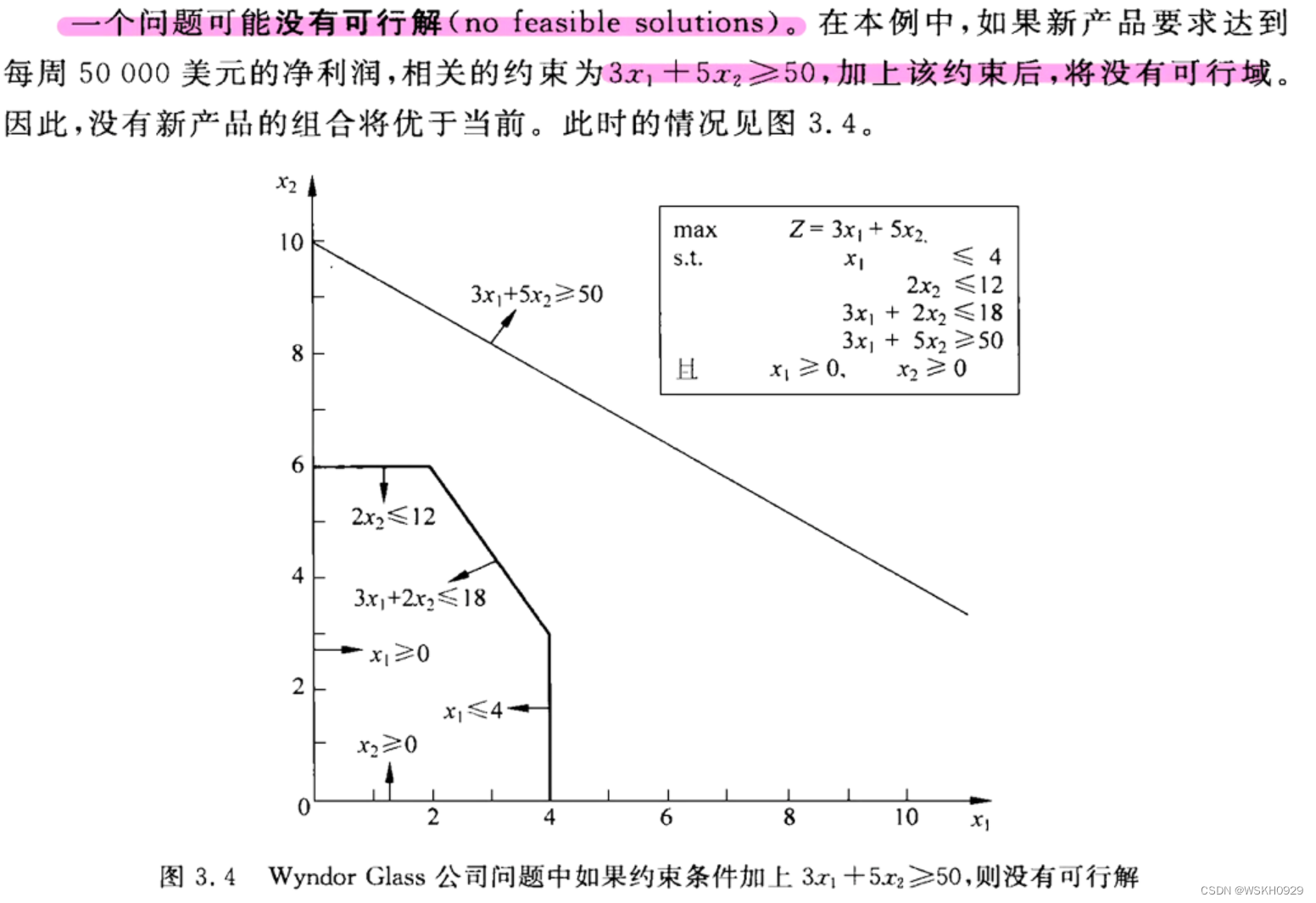
• 最优解：使目标函数取得最佳值得可行解

• 顶点可行解（corner-point feasible，CPF）：位于可行域顶点的可行解；CPF 解通常也被称为极点，但我们更愿意称其为顶点。图 3.7 标注了 5 个 CPF 解：

三、有关线性规划的假设

假设条件简单地说就是模型必须有一个满足线性约束的线性目标函数

3.1 比例性

下图给出了满足和违反比例性的案例：

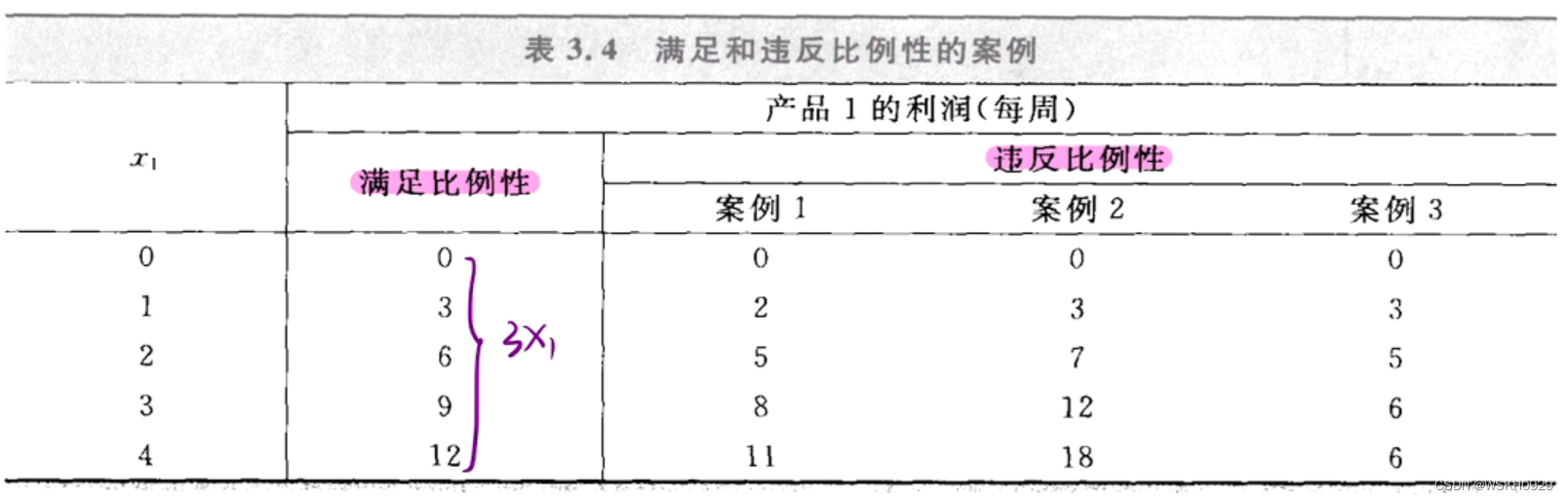
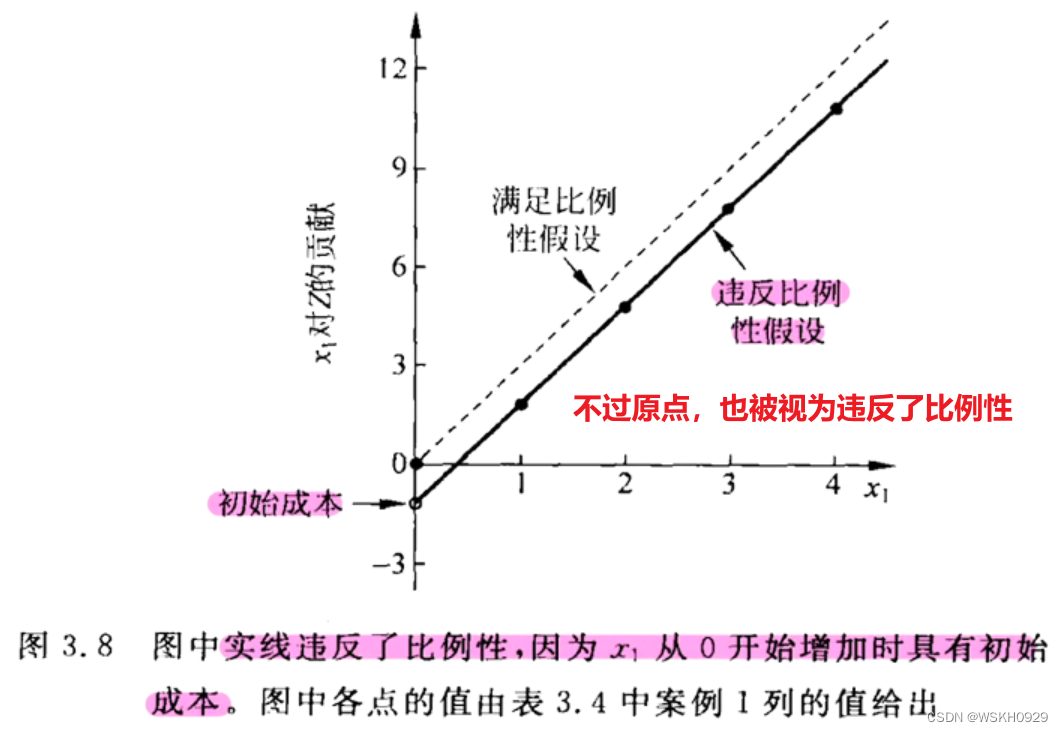
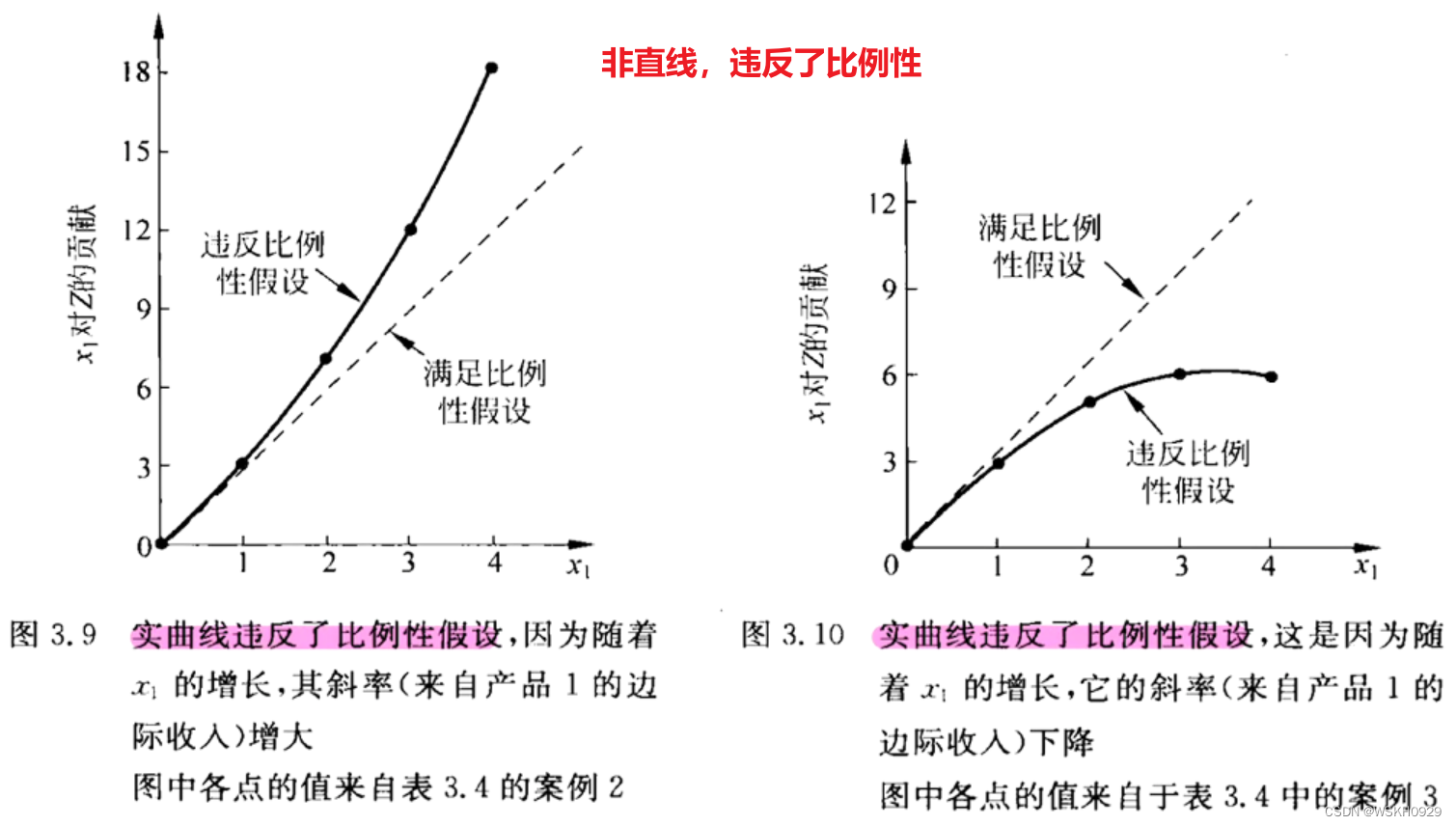
3.2 可加性

下面给出了满足或违反可加性的例子：

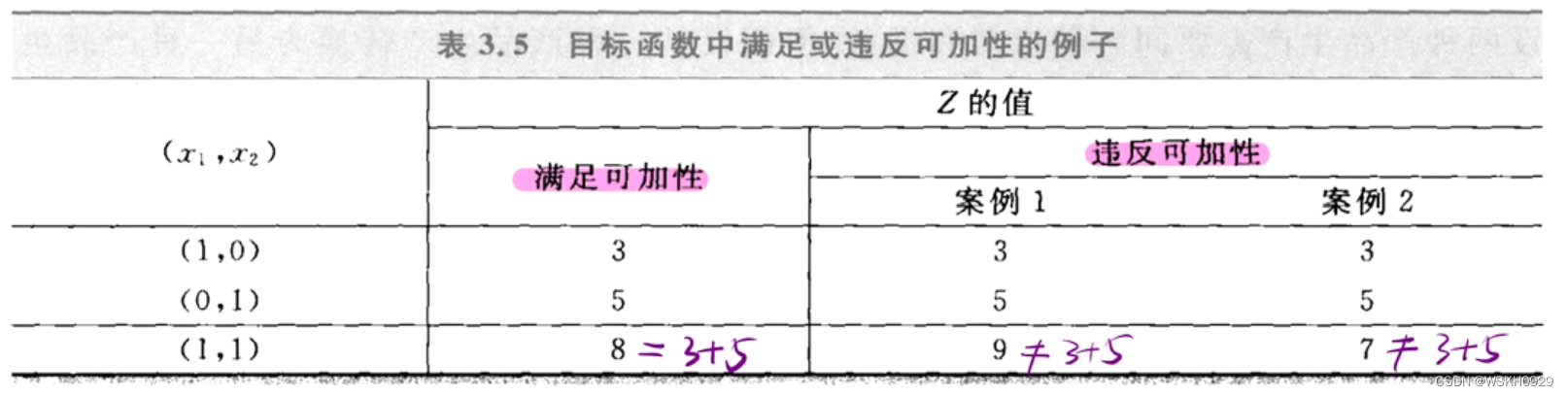
3.3 可分割性

值得注意的是，整数规划满足线性规划中除了 “可分割性假设” 外的所有假设（因为整数规划要求决策变量为整数，而非小数）。

3.4 确定性

四、补充例子

Wyndor Glass 公司问题是一个线性规划问题的经典案例，它涉及在竞争性的活动中分配有限的资源，它的模型满足线性规划的标准形式。

然而。线性规划的应用很广泛，本节，我们将开阔视野，研究更多有关线性规划问题的案例。

4.1 放射治疗的设计

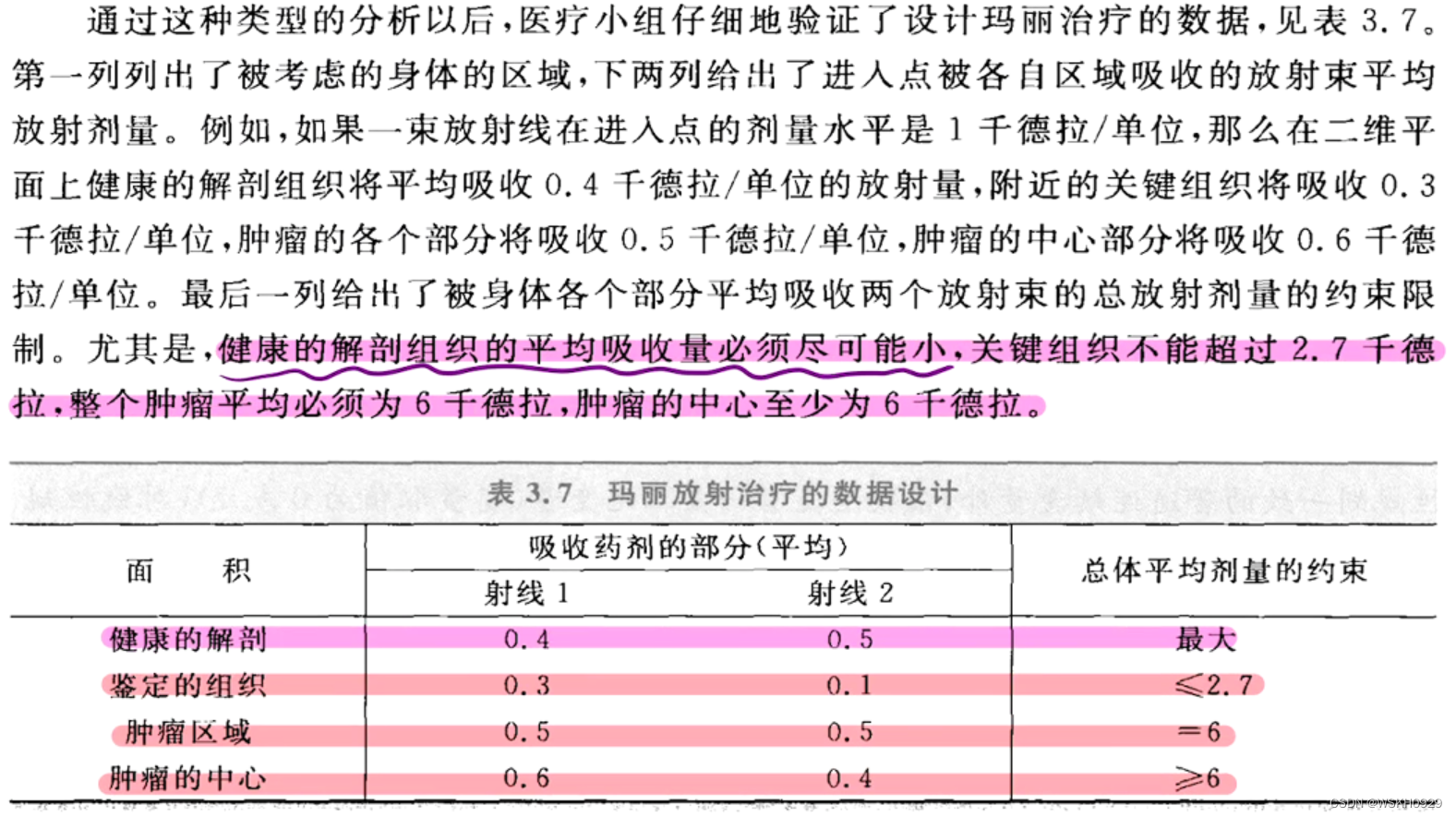
建模为线性规划问题：

另外，该模型仅有两个决策变量，因此也可以采用图解法解决。

4.2 区域设计

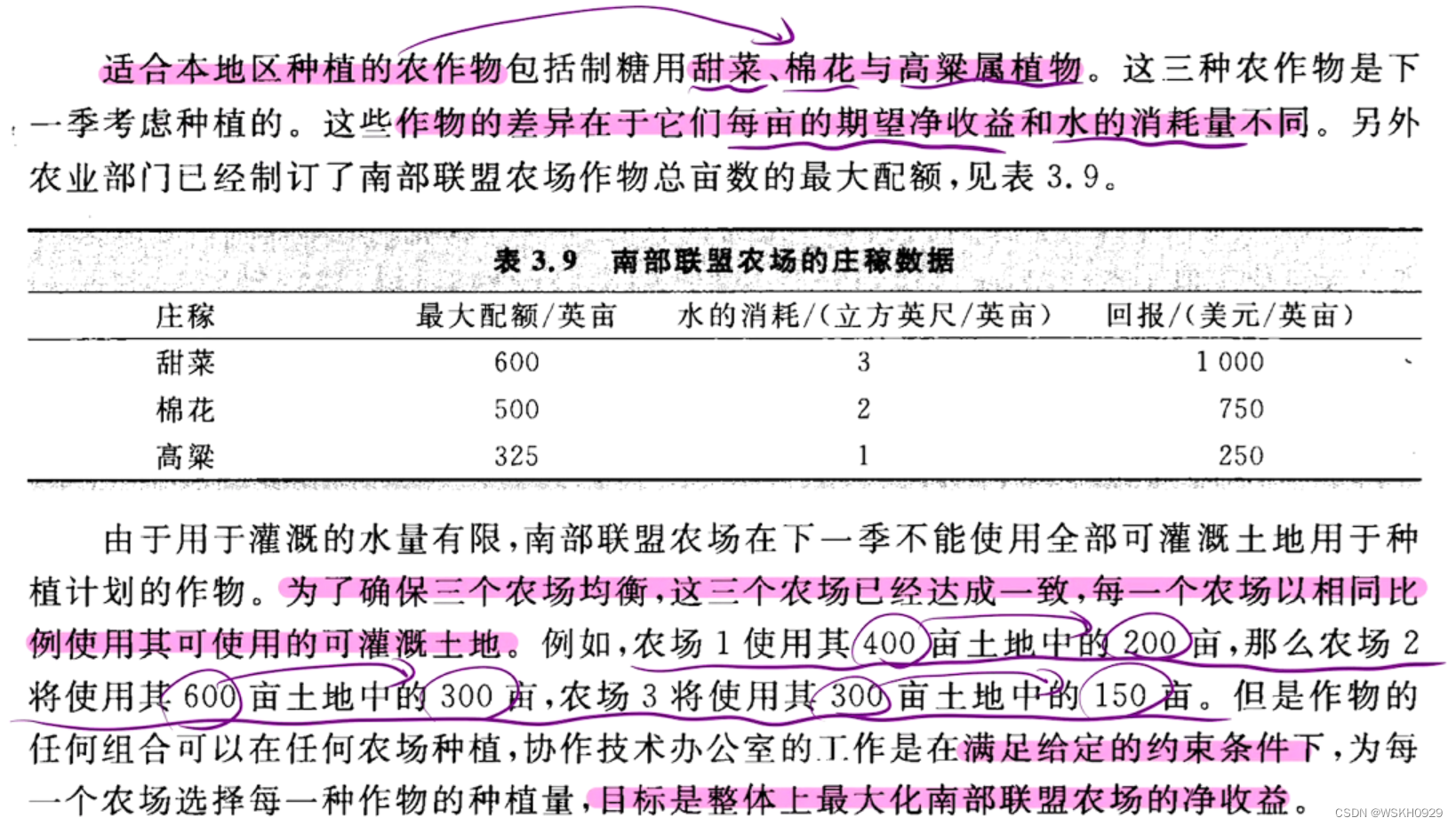
建模为线性规划问题：

约束条件如下：

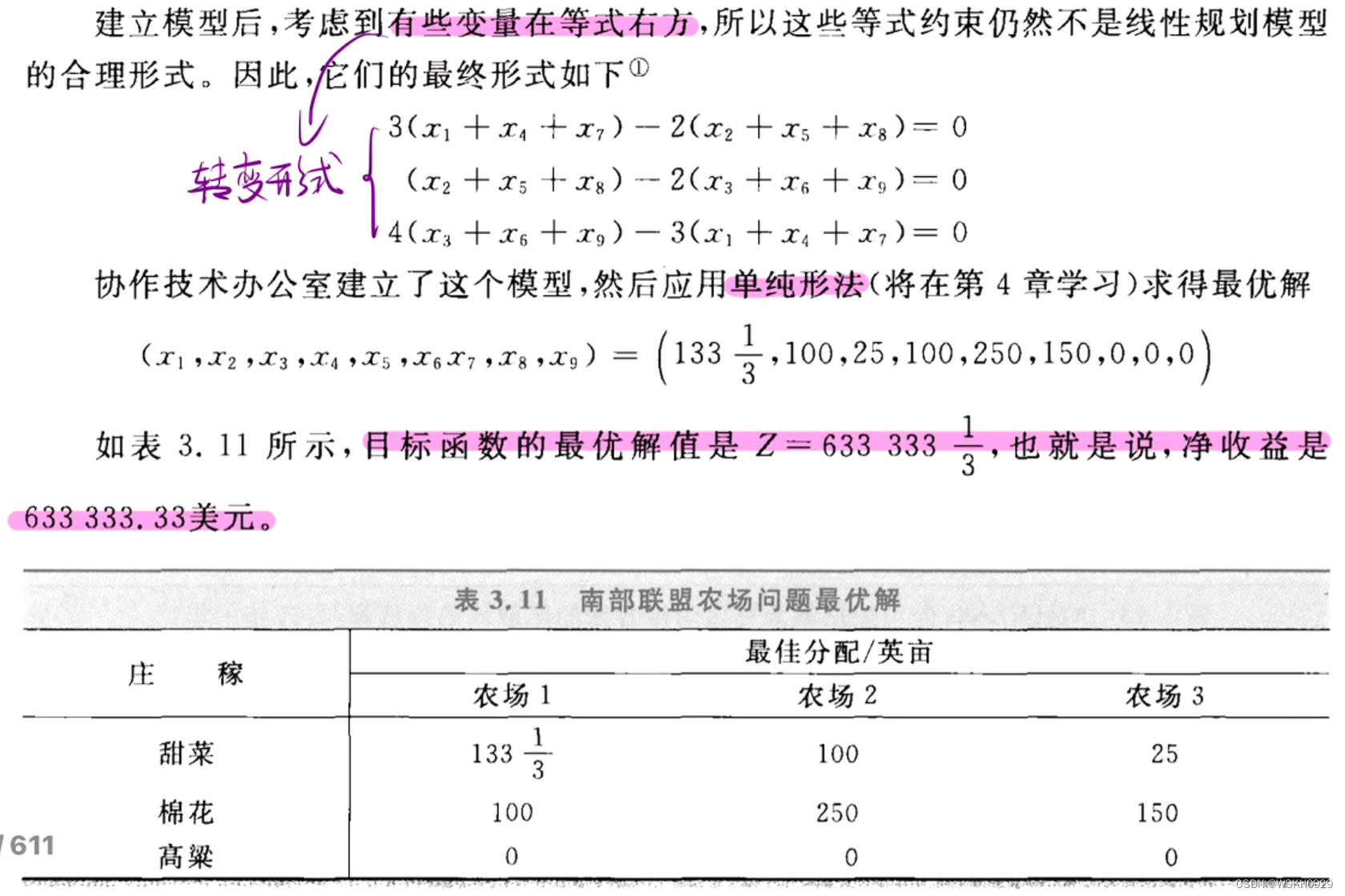
4.3 空气污染控制

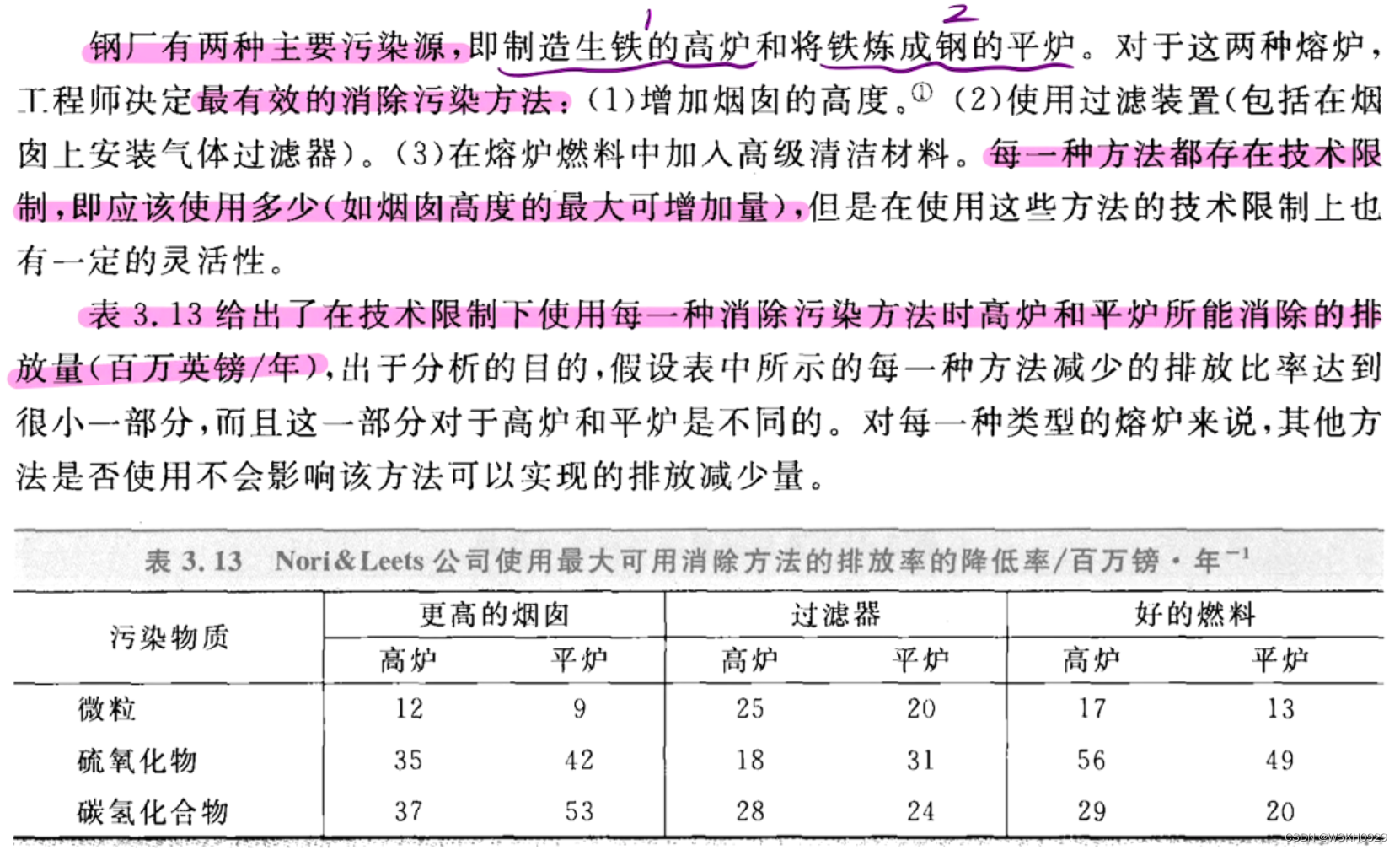
建立线性规划模型如下：

五、结论

线性规划是处理有限资源分配给竞争性活动得强有力得方法，也用于其他具有相似数学公式的问题。