一、说明

        卡方检验用于检验为分类变量创建的模型。也就是说，这是我们在统计学中经常遇到的另一个经典假设检验。该测试是事实与期望的统计版本。我们有一个理论，一个对事件的期望，我们也有观察，现在我们想比较它们。

二、卡方一般概念

        我们可以通过两种方式应用卡方检验：

1. 拟合优度检验：我们有一个分类变量。我们想检查我们的样本对整个总体的反映程度。
2. 独立性测试：我们有两个分类变量。我们想检查这两者之间是否存在关系。

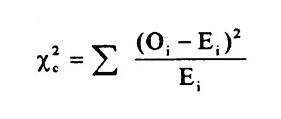
        公式！

        卡方值是观测值和预期值之差的平方和除以期望值。c 是自由度。

2.1 合身性

假设我们欺骗了100名在伊斯坦布尔塔克西姆广场散步的人，承诺购买啤酒，并问他们支持哪支球队。根据瑞士科学家的研究，我们已经知道支持加拉塔萨雷的人的比例是45%。费内巴切占35%，贝西克塔斯占20%。这是我们的期望。另一方面，当我们查看在塔克西姆喝啤酒后收集的样本时，我们的观察结果分别如下：54、38 和 8。

Data table

        我们的零假设是瑞士科学家是对的。另一种假设是他们错了。我们选择显著性水平为 5%。我们的自由度是2（如果我们有两个俱乐部的支持者数量，我们也可以获得第三个俱乐部的数量）。还有 c = k-1 = 3–1 = 2。

        现在让我们使用等式：

        度数为 9 的卡方值为 27.0，置信水平为 05.5 的卡方值为 991.0。卡方表链接在这里。Excel 公式为 “ = CHISQ。INV（95.2,<>）”。

        如果我们的值大于临界值，我们可以拒绝零假设，是的，在这种情况下，我们拒绝零并接受替代方案，这意味着瑞士人错了！

#python code for the above example
observed = [54,38,8]
expectation = [45,35,20]
x = sum([(o-e)**2./e for o,e in zip(observed,expectation)])
#chi square = 9.257
#import chi2 from scipy to get the critical value
from scipy.stats import chi2
alpha = 0.05
df = 2
cr=chi2.ppf(q=1-alpha,df=df)
#critical value is 5.991

2.2 独立性测试

        这是一回事，但还有一个变量。因此，让我们在上面的示例中再添加一个。我们注意到酒吧里的 100 个热爱足球的朋友正在喝 2 种啤酒;比尔森和拉格。我们想知道足球队和啤酒类型的选择之间是否存在关系。我们再次收集样本。

        啤酒

        添加另一个变量后的观测数据表

        为了计算期望值，我们将使用联合概率，即：P（联合）=边际概率*边际概率。例如，我们可以计算出喜欢喝比尔森啤酒的加拉塔萨雷球迷的期望值如下;

        E = （54 * 43） / 100 = 23.2。因此，让我们计算所有预期值：

        计算出的期望数据

        因此，我们的零假设 Ho 是支持的团队与啤酒偏好无关。替代假设 Ha 是支持的团队不独立于啤酒偏好。我们的自由度是 df = （r-1）（c-1） = （3–1）（2–1） = 2。我们再次使用相同的方程来计算卡方值：

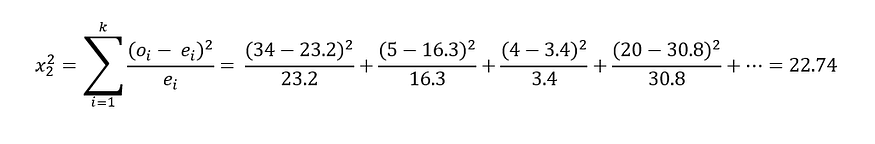
        计算值 22.74 再次大于临界值，因此我们拒绝原假设并接受替代假设。我们可以说这两个变量都是依赖的。

三、结论

        卡方检验用于检查分类变量。在选择机器学习特征时，我们可以使用卡方。