排名评估指标综合指南

一、介绍

右排序是机器学习中的一个问题，其目标是以最合适的方式对最终用户的文档列表进行排序，因此最相关的文档出现在顶部。排名出现在数据科学的多个领域中，从推荐系统开始，算法建议一组要购买的商品，最后到 NLP 搜索引擎，根据给定的查询，系统尝试返回最相关的搜索结果。

自然出现的问题是如何估计排名算法的质量。与经典机器学习一样，不存在适合任何类型任务的单一通用指标。为什么？原因很简单，因为每个指标都有自己的应用范围，这取决于给定问题的性质和数据特征。

这就是为什么了解所有主要指标对于成功解决任何机器学习问题至关重要。这正是我们在本文中要做的事情。

尽管如此，在继续之前，让我们了解为什么某些流行指标通常不应该用于排名评估。通过考虑这些信息，将更容易理解其他更复杂的指标存在的必要性。

注意。本文和使用的公式基于Ilya Markov 的离线评估演示。

二、指标

我们将在本文中讨论几种类型的信息检索指标：

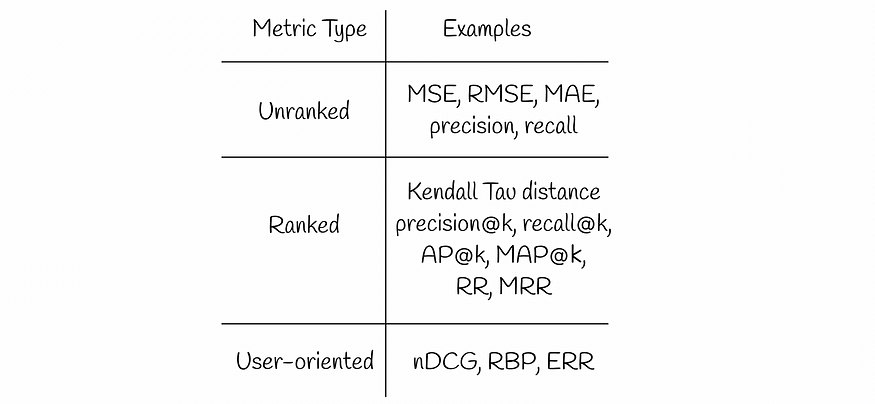
不同类型的指标

三、未排名指标

想象一下一个推荐系统可以预测电影的评分并向用户展示最相关的电影。评级通常代表正实数。乍一看，像MSE（RMSE、MAE等）这样的回归指标似乎是在保留数据集上评估系统质量的合理选择。

MSE考虑所有预测的电影并测量真实标签和预测标签之间的平均平方误差。然而，最终用户通常只对出现在网站首页上的顶部结果感兴趣。这表明他们对出现在搜索结果末尾的评分较低的电影并不真正感兴趣，这些电影也同样通过标准回归指标进行估计。

下面的一个简单示例演示了一对搜索结果并测量每个结果的MSE值。

两个查询的错误估计表明 MSE 是一个不好的排名指标。绿色文件是相关的，而红色文件是不相关的。文档列表按预测相关性的顺序显示（从左到右）。

尽管第二搜索结果具有较低的MSE，但是用户不会对这样的推荐感到满意。通过首先仅查看不相关的项目，用户将必须一直向上滚动才能找到第一个相关的项目。这就是为什么从用户体验的角度来看，第一个搜索结果要好得多：用户只是对最上面的项目感到满意，然后继续搜索它，而不关心其他项目。

同样的逻辑也适用于分类指标（精确度、召回率），它也考虑所有项目。

精确率和召回率公式

所有描述的指标有什么共同点？他们都平等地对待所有项目，并且不考虑高相关性结果和低相关性结果之间的任何区别。这就是为什么他们被称为无等级的。

通过上面这两个类似的有问题的例子，我们在设计排名指标时应该关注的方面似乎更加清晰：

排名指标应该更加重视更相关的结果，同时降低或忽略不太相关的结果。

四、排名指标

4.1 肯德尔·陶距离

Kendall Tau 距离基于秩反转的次数。

倒排是一对文档（i，j），例如文档i比文档j具有更大的相关性，在搜索结果上出现在j之后。

Kendall Tau 距离计算排名中所有倒转的次数。反转次数越少，搜索结果越好。尽管该指标可能看起来合乎逻辑，但它仍然有一个缺点，如下例所示。

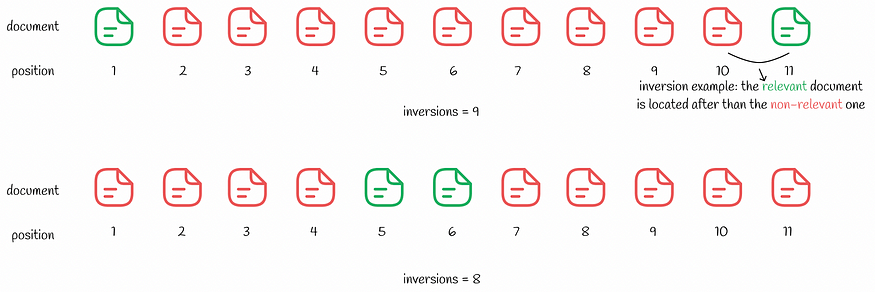
尽管反转次数较少，但从用户角度来看，第二名的排名仍然较差

看起来第二个搜索结果更好，只有 8 个反转，而第一个搜索结果有 9 个。与上面的MSE示例类似，用户只对第一个相关结果感兴趣。通过在第二种情况下浏览几个不相关的搜索结果，用户体验会比第一种情况更差。

4.2 精确度@k 和召回率@k

可以仅考虑一定数量的顶级推荐k ，而不是通常的精度和召回率。这样，该指标就不会关心排名较低的结果。根据所选的k值，相应的度量分别表示为precision@k（“k 处的精度”）和recall@k（“k 处的召回率”）。它们的公式如下所示。

precision@k 和recall@k 公式

想象一下，向用户显示前k 个结果，其中每个结果可能相关，也可能不相关。precision@k衡量前k个结果中相关结果的百分比。同时，recall@k评估前k 个相关结果占整个数据集中相关项目总数的比例。

为了更好地理解这些指标的计算过程，让我们参考下面的例子。

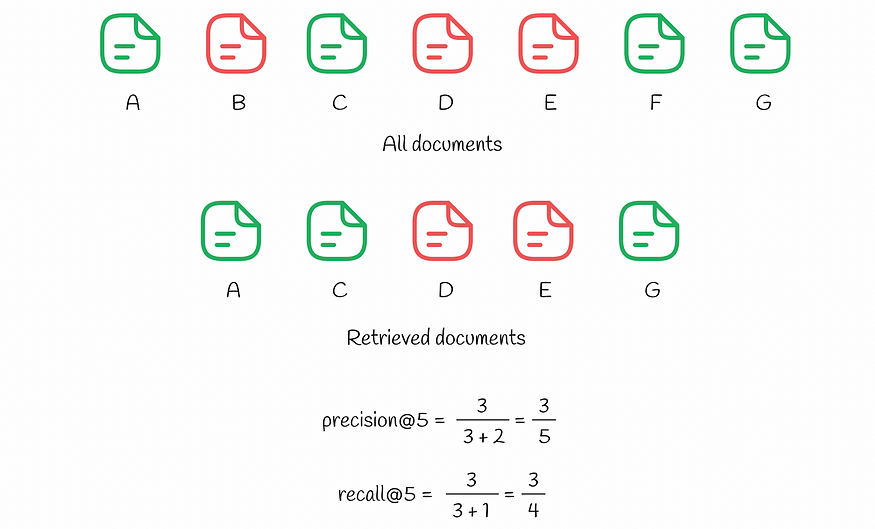
precision@k和recall@k计算示例。绿色文档代表相关项目，红色文档对应不相关项目。

系统中有7个文档（名称从A到G）。根据预测，算法为用户选择其中k = 5 个文档。我们可以注意到， top k = 5中有 3 个相关文档（A、C、G），这导致precision@5等于3 / 5。同时，recall@5考虑了整个数据集中的相关项：其中有 4 个（A、C、F和G），使得recall@5 = 3 / 4。

召回@k总是随着k的增长而增加，使得这个指标在某些情况下并不真正客观。在向用户显示系统中的所有项目的边缘情况下， recall@k的值等于 100%。precision@k不具有与recall@k相同的单调属性，因为它衡量与前k个结果相关的排名质量，而不是与整个系统中相关项目的数量相关。在实践中，客观性是precision@k通常比recall@k更受青睐的指标的原因之一。

4.3 AP@k（平均精度）和 MAP@k（平均精度）

vanilla precision@k的问题在于它没有考虑检索到的文档中出现的相关项目的顺序。例如，如果有 10 个检索到的文档，其中 2 个相关，则尽管这 2 个文档在 10 个文档中的位置，精度@10将始终相同。例如，如果相关项位于位置(1, 2)或(9, 10)，该度量确实区分了这两种情况，导致precision@10等于 0.2。

然而，在现实生活中，系统应该对排在顶部而不是底部的相关文档给予更高的权重。这个问题可以通过另一个称为平均精度( AP )的指标来解决。作为普通精度，AP取 0 到 1 之间的值。

平均精度公式

AP@k计算与第i个文档相关的从 1 到k的所有i值的precision@i平均值。

为两个查询计算的平均精度

在上图中，我们可以看到相同的7个文档。对查询Q₁ 的响应导致k = 5 个检索到的文档，其中 3 个相关文档位于索引(1, 3, 4)处。对于每个位置i，计算precision@i ：

精度@1 = 1 / 1
精度@3 = 2 / 3
精度@4 = 3 / 4

所有其他不匹配的索引i 都将被忽略。AP@5的最终值计算为上述精度的平均值：

AP@5 = (精度@1 + 精度@3 + 精度@4) / 3 = 0.81

为了进行比较，让我们看看另一个查询Q2的响应，它也包含前k个中的 3 个相关文档。然而，这一次，2 个不相关的文档位于顶部（位置(1, 3)）比之前的情况更高，这导致较低的AP@5等于 0.53。

有时需要评估算法的质量，而不是在单个查询上，而是在多个查询上。为此，使用平均精度 ( MAP ) 。Is 只是取多个查询Q中AP的平均值：

平均精度公式

下面的示例显示了如何为 3 个不同的查询计算MAP ：

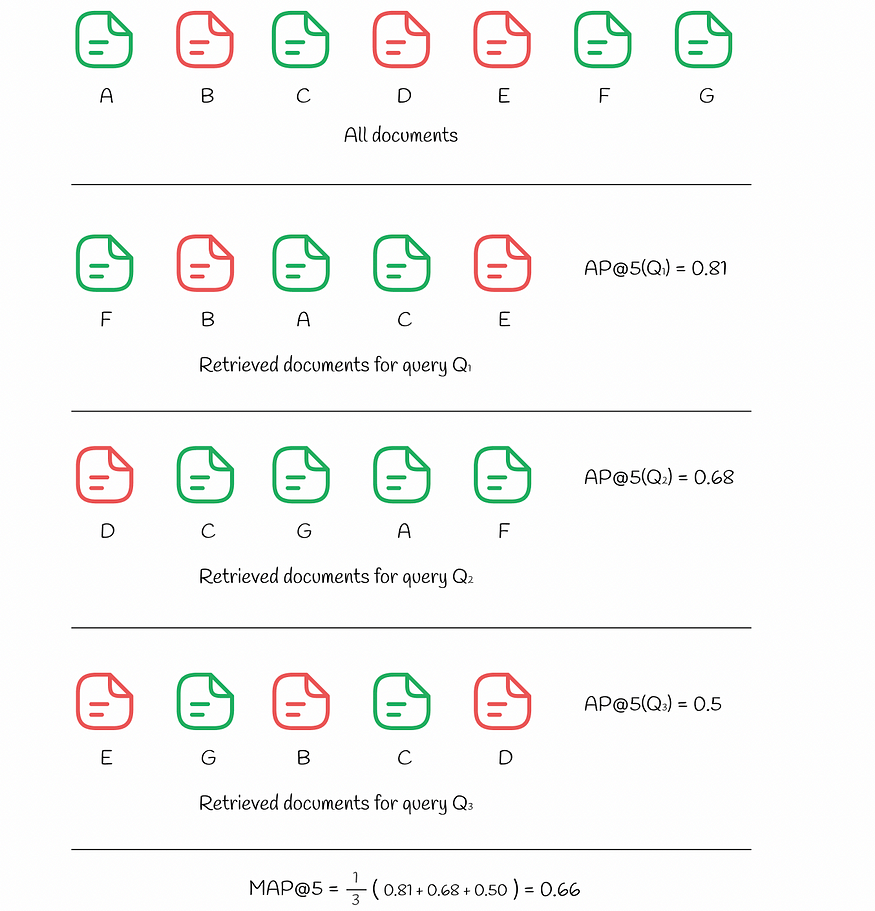
为三个查询计算的 AP 和 MAP

4.4 RR（倒数排名）和 MRR（平均倒数排名）

有时用户只对第一个相关结果感兴趣。倒数排名是一个度量，它返回 0 到 1 之间的数字，指示第一个相关结果距离顶部有多远：如果文档位于位置k ，则RR的值为1 / k。

与AP和MAP类似，平均倒数排名 (MRR)衡量多个查询之间的平均RR 。

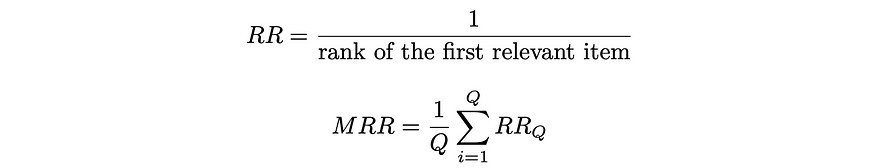
RR 和 MRR 公式

下面的示例显示了如何计算 3 个查询的RR和MRR ：

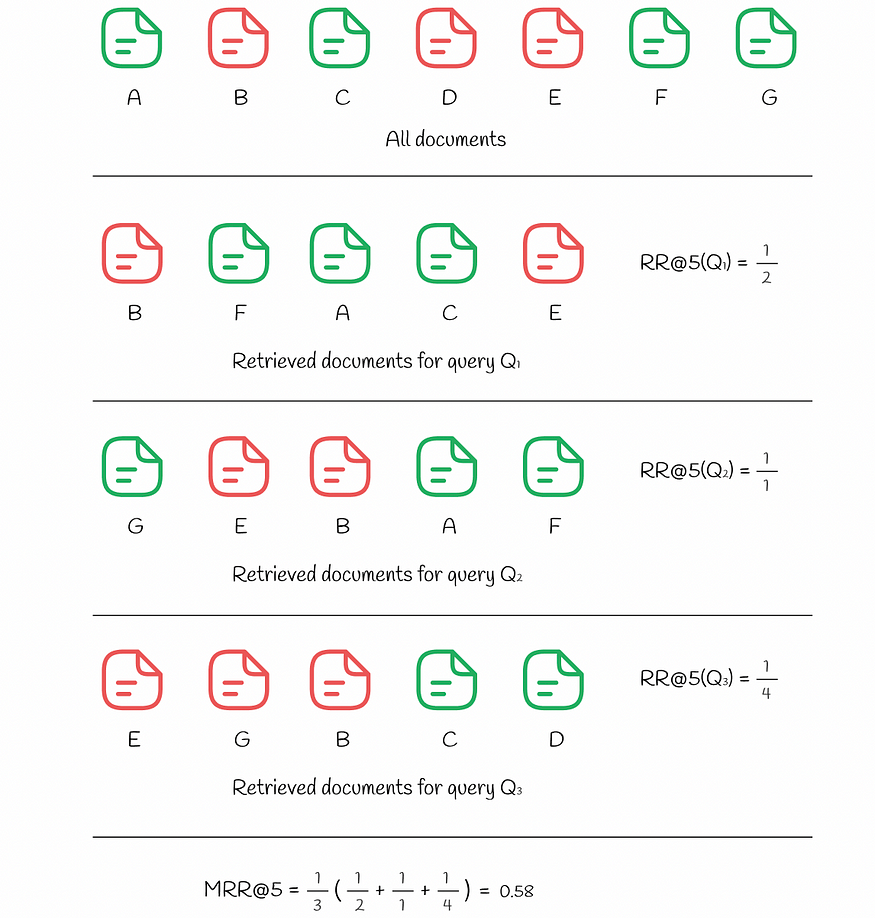
为三个查询计算的 RR 和 MRR

五、以用户为导向的指标

尽管排名指标考虑了项目的排名位置，因此比未排名的指标是更好的选择，但它们仍然有一个显着的缺点：没有考虑有关用户行为的信息。

面向用户的方法对用户行为做出某些假设，并在此基础上产生更适合排名问题的指标。

5.1 DCG（贴现累积增益）和 nDCG（标准化贴现累积增益）

DCG 指标的使用基于以下假设：

高度相关的文档在搜索引擎结果列表中较早出现时更有用（具有更高的排名） -维基百科

这种假设自然代表了用户如何评估较高的搜索结果（与较低的搜索结果相比）。

在DCG中，每个文档都分配有一个增益，该增益指示特定文档的相关程度。给定每个项目的真实相关性Rᵢ（实际值），有多种方法来定义增益。最流行的之一是：

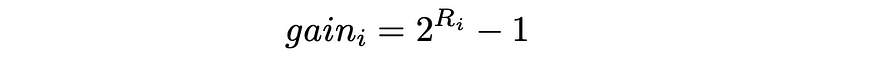
DCG 中可能的增益公式

基本上，指数非常强调相关项目。例如，如果为一部电影的评分分配了 0 到 5 之间的整数，则与评分减少 1 的电影相比，具有相应评分的每部电影的重要性大约会增加一倍：

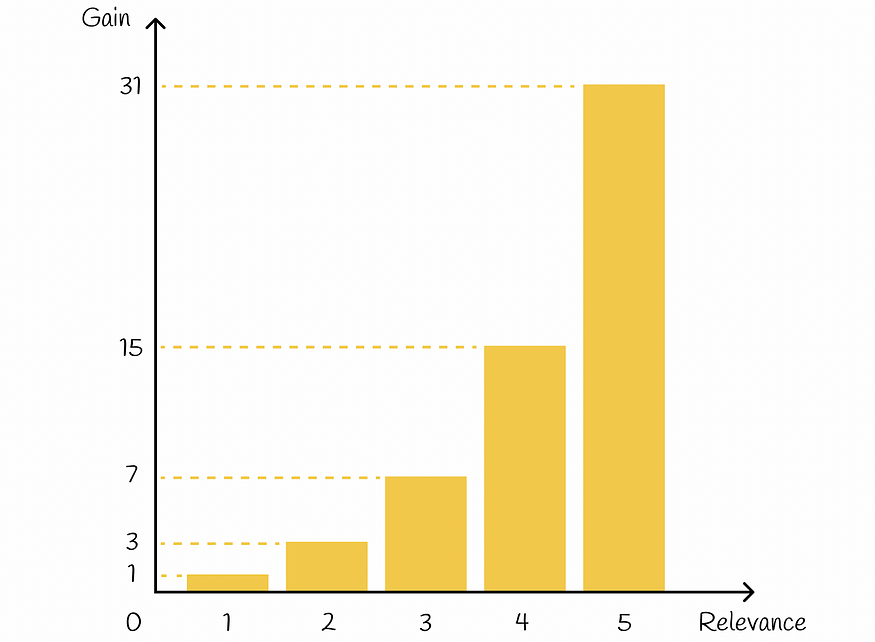
获得相关性函数

除此之外，根据排名，每件商品都会获得一个折扣值：排名越高的商品，相应的折扣就越高。折扣通过按比例减少商品的收益来起到惩罚作用。在实践中，折扣通常选择为排名指数的对数函数：

DCG 中的折扣公式

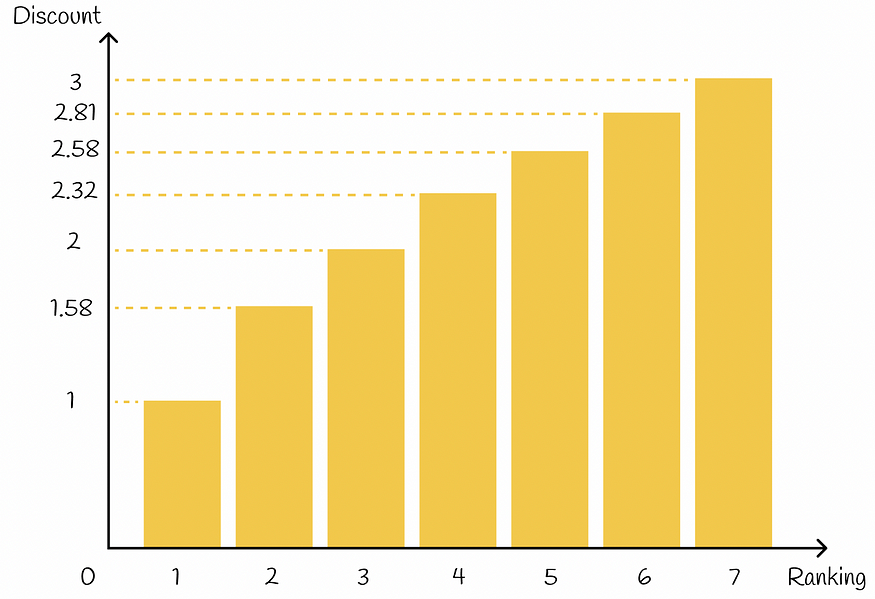
排名折扣功能

最后，DCG@k被定义为所有前 k 个检索到的项目的折扣增益之和：

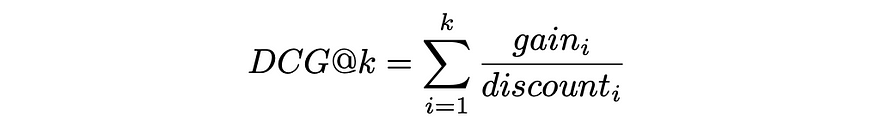
DCG 公式一般

将gainᵢ和discountᵢ替换为上面的公式，表达式采用以下形式：

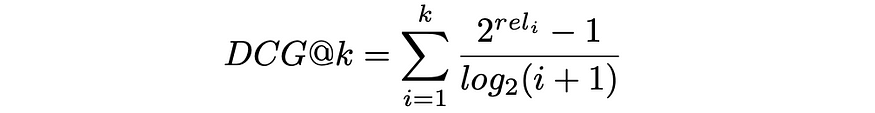
DCG公式

为了使DCG指标更具可解释性，当所有项目均按其相关性正确排序时，在完美排名的情况下，通常通过DCGₘₐₓ的最大可能值对其进行归一化。生成的度量称为nDCG，其值介于 0 和 1 之间。

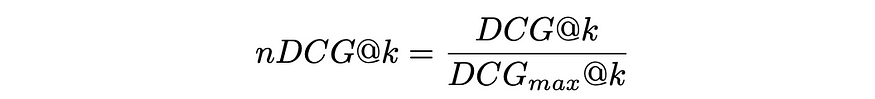
nDCG公式

下图显示了5个文档的DCG和nDCG计算示例。

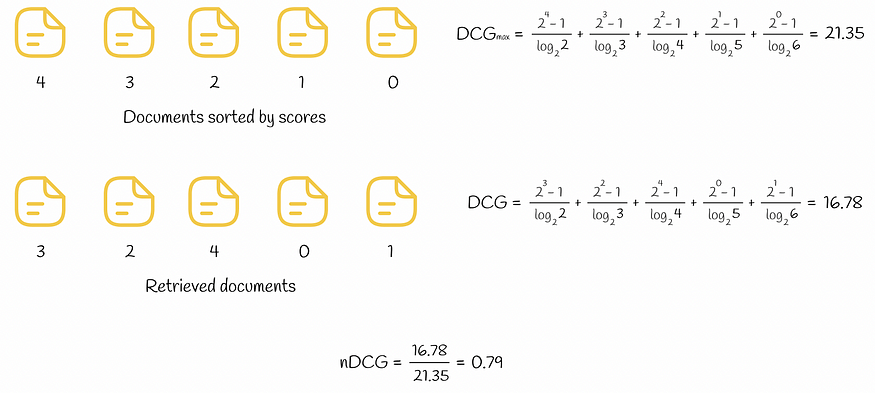
为一组检索到的文档计算的 DCG 和 nDCG

5.2 RBP（排名偏向精度）

在RBP工作流程中，用户无意检查每个可能的项目。相反，他或她以概率p顺序从一个文档前进到另一个文档，并以逆概率1 - p终止当前文档的搜索过程。每个终止决定都是独立做出的，不依赖于搜索的深度。根据所进行的研究，在许多实验中都观察到了这种用户行为。根据检索有效性测量的排名偏差精度中的信息，工作流程如下图所示。

参数 p 称为持久性。

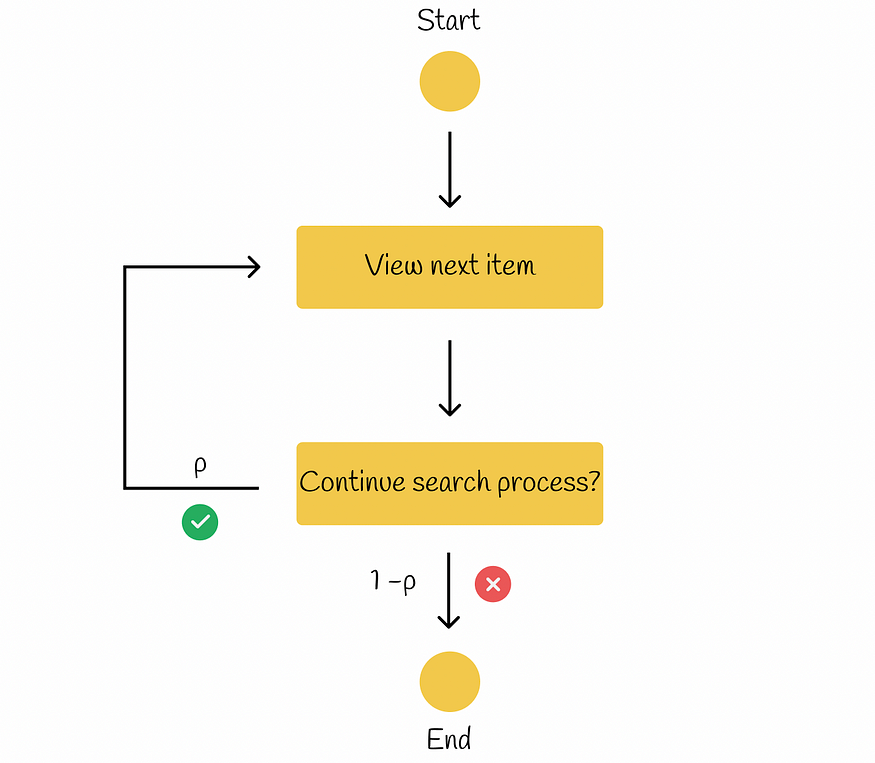
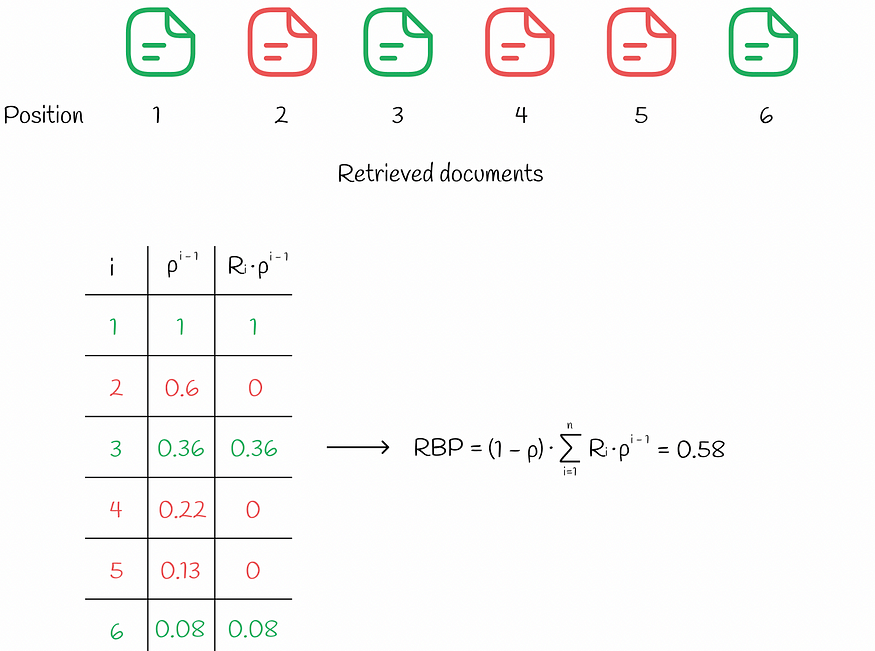
RBP 模型工作流程

在此范例中，用户总是查看第1个文档，然后以p的概率查看第2个文档，以p²的概率查看第3个文档，依此类推。最终，查看文档i的概率等于：

仅当文档i刚刚被查看时，用户才检查文档i ，并且搜索过程以概率1_p立即终止。

之后，就可以估计预计检查的文件数量。由于0 ≤ p ≤ 1，下面的级数是收敛的，表达式可以转换为以下格式：

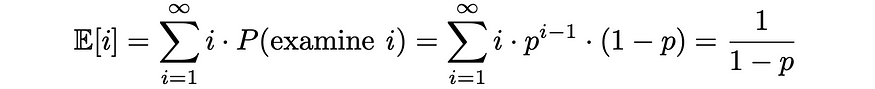
同样，给定每个文档的相关性Rᵢ，让我们找到预期的文档相关性。预期相关性值越高表明用户对其决定检查的文档越满意。

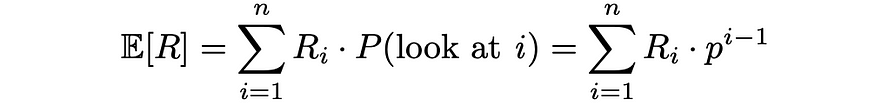
最后，RPB计算为预期文档相关性（效用）与预期已检查文档数量的比率：

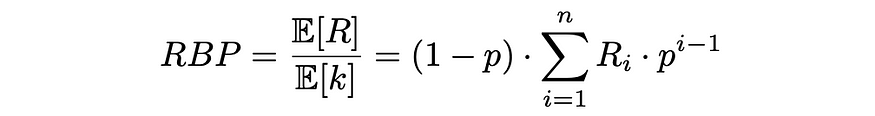
RPB公式确保它采用 0 到 1 之间的值。通常，相关性分数是二进制类型（如果文档相关则为 1，否则为 0），但也可以采用 0 到 1 之间的实际值。

应根据用户在系统中的持久程度来选择适当的p值。p值较小（小于 0.5）会更加强调排名中排名靠前的文档。随着p值的增大，第一个位置的权重会减少并分布在较低的位置上。有时可能很难找出持久性p的良好值，因此最好进行多次实验并选择效果最好的p 。

5.3 ERR（预期倒数排名）

顾名思义，该指标衡量许多查询的平均倒数排名。

该模型与RPB类似，但有一点区别：如果当前项目与用户相关（Rᵢ ），则搜索过程结束。否则，如果该项目不相关 ( 1 — Rᵢ)，则用户以概率p决定他或她是否要继续搜索过程。如果是，则搜索继续到下一项。否则，用户结束搜索过程。

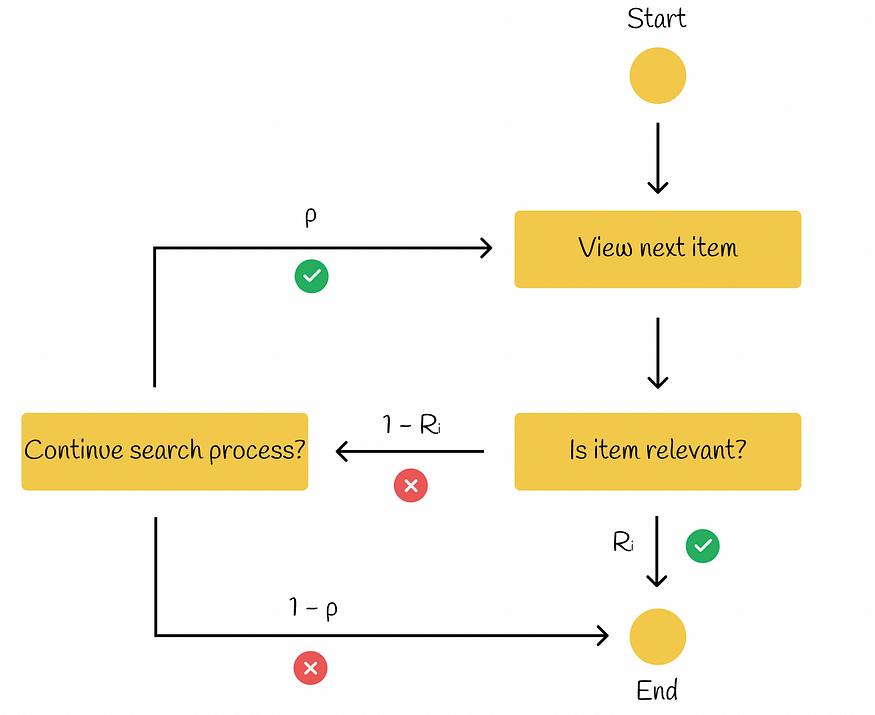
ERR模型工作流程

根据Ilya Markov关于离线评估的介绍，让我们找到ERR的计算公式。

首先，让我们计算用户查看文档 i 的概率。基本上，这意味着所有i-1 个先前文档都不相关，并且在每次迭代中，用户以概率 p 继续下一个项目：

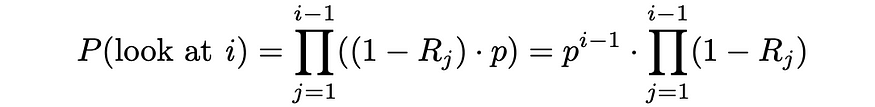
如果用户停在文档i处，则意味着该文档已经被查看过，并且以概率Rᵢ，用户决定终止搜索过程。该事件对应的概率实际上是相同的，倒数等级等于1 / i。

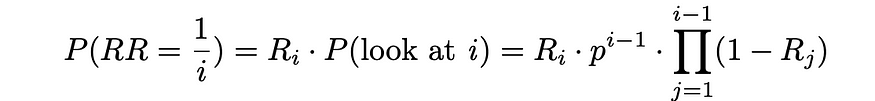
从现在开始，只需使用期望值的公式，就可以估计期望的倒数排名：

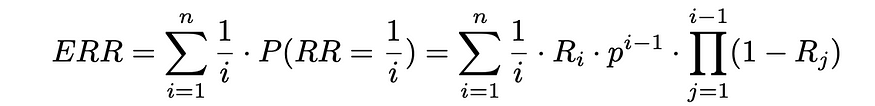
参数 p 通常选择接近 1。

与RBP的情况一样， Rᵢ的值可以是二进制，也可以是 0 到 1 范围内的实数。下图演示了一组 6 个文档的ERR计算示例。

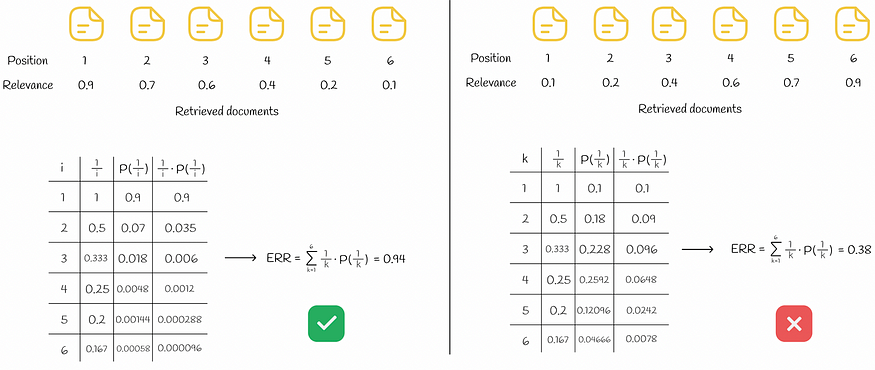
错误率计算。最好和最差的排名分别显示在左侧和右侧。为简单起见，参数 p 选择为 1。

在左侧，所有检索到的文档均按其相关性降序排序，从而获得最佳的ERR。与右侧的情况相反，文档按其相关性的升序排列，从而导致最糟糕的ERR。

ERR 公式假设所有相关性分数都在 0 到 1 的范围内。如果给出的初始相关性分数超出该范围，则需要对它们进行标准化。最流行的方法之一是将它们指数标准化：

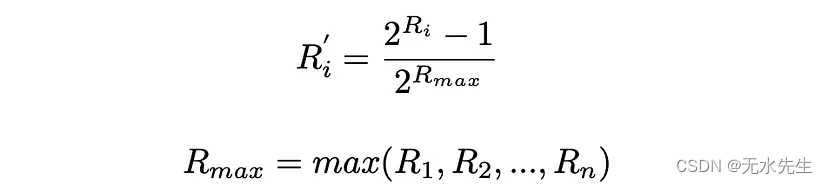
六、结论

我们已经讨论了信息检索中用于质量评估的所有主要指标。面向用户的指标被更频繁地使用，因为它们反映了真实的用户行为。此外，nDCG、BPR和ERR指标比我们迄今为止研究过的其他指标具有优势：与仅针对二进制级别设计的AP 、 MAP或MRR等指标相比，它们适用于多个相关级别，使它们更加通用。关联。

不幸的是，所有描述的指标要么是不连续的，要么是平坦的，使得有问题的点处的梯度等于 0，甚至没有定义。因此，大多数排名算法很难直接优化这些指标。然而，在这个领域已经进行了大量的研究，并且在最流行的排名算法的背后出现了许多先进的启发式方法来解决这个问题。