一、说明
相似性搜索是一个问题,给定一个查询,目标是在所有数据库文档中找到与其最相似的文档。 在数据科学中,相似性搜索经常出现在 NLP 领域、搜索引擎或推荐系统中,其中需要检索最相关的文档或项目以进行查询。有多种不同的方法可以提高海量数据的搜索性能。
在上一部分中,我们研究了 LSH 的主要范例,即将输入向量转换为低维哈希值,同时保留有关其相似性的信息。为了获取哈希值(签名),使用了 minhash 函数。在本文中,我们将随机投影输入数据以获得类似的二进制向量。
二、主要原理
考虑高维空间中的一组点。可以构造一个随机超平面,充当墙并将每个点分为两个子组之一:正子组和负子组。正侧的各点被赋予“1”值,负侧的各点被赋予“0”值。
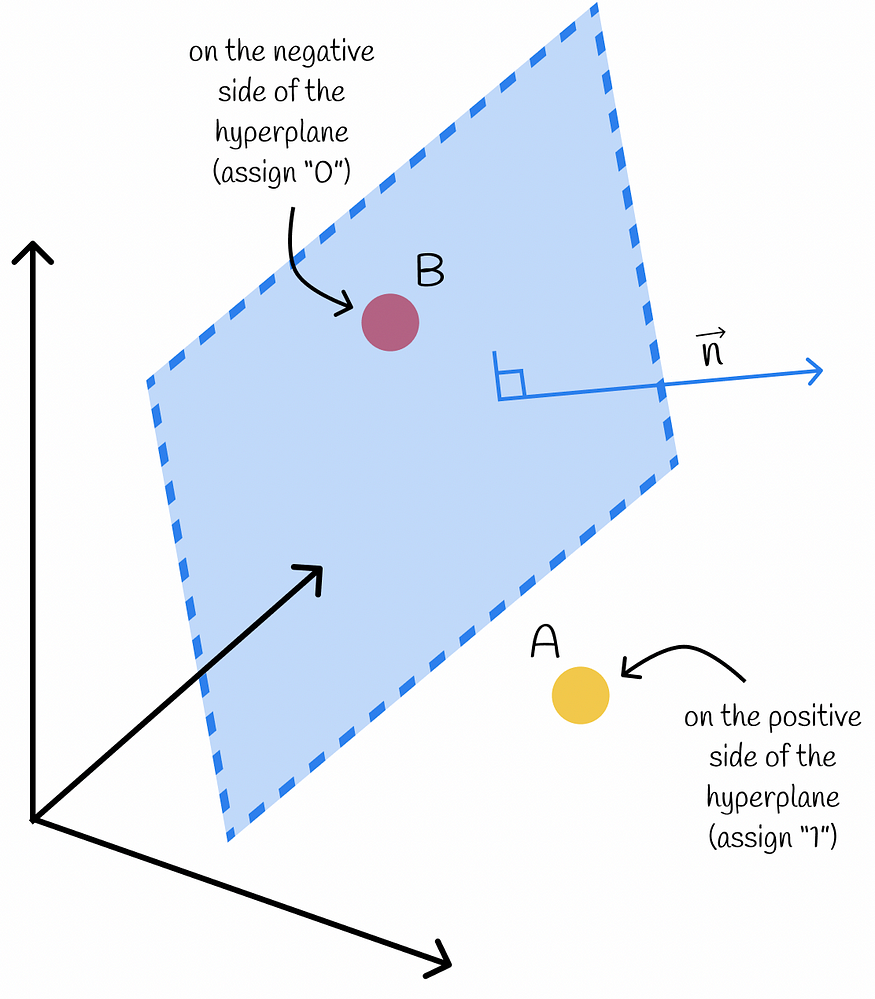
如何确定某个向量的超平面的边?通过使用内积!回到线性代数的本质,给定向量与超平面法向量之间的点积的符号决定了该向量位于哪一侧。这样,每个数据集向量都可以分为两侧之一。

计算向量与超平面法向量的内积,并与0比较,可以知道向量相对于超平面位于哪一侧
显然,用一个二进制值对每个数据集向量进行编码是不够的。也就是说,应该构造几个随机超平面,因此每个向量都可以根据其与特定超平面的相对位置用许多 0 和 1 值进行编码。如果两个向量具有完全相同的二进制代码,则表明所构造的超平面都无法将它们分成不同的区域。因此,他们在现实中很可能非常接近。
为了找到给定查询的最近邻居,通过检查其与所有超平面的相对位置以相同的方式用 0 和 1 编码查询就足够了。可以将找到的查询二元向量与为数据集向量获得的所有其他二元向量进行比较。这可以通过使用汉明距离线性完成。
两个向量之间的汉明距离是它们的值不同的位置的数量。
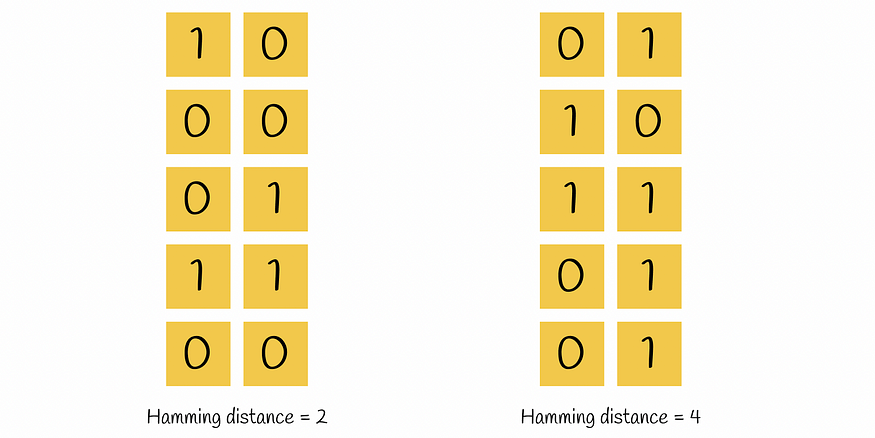
计算汉明距离的示例。左边的一对向量彼此更相似,因为它们的汉明距离更小。与查询的汉明距离最小的二元向量被视为候选向量,然后与初始查询进行充分比较。
2.1 为什么超平面是随机构建的?
在当前阶段,要求为什么超平面以随机方式构建而不是确定性意味着可以定义用于分离数据集点的自定义规则似乎是合乎逻辑的。这背后有两个主要原因:
- 首先,确定性方法无法推广算法并可能导致过度拟合。
- 其次,随机性允许对算法的性能做出不依赖于输入数据的概率陈述。对于确定性方法来说,这是行不通的,因为它可能对一个数据表现良好,但对另一数据表现不佳。一个很好的类比是确定性快速排序算法,其平均运行时间为O(n * log n) 。然而,在最坏的情况下,它在排序数组上的时间复杂度为O(n²) 。如果有人了解算法的工作流程,那么该信息可以通过始终提供最坏情况的数据来明显损害系统的效率。这就是为什么随机快速排序更受欢迎的原因。随机超平面也会发生绝对类似的情况。
2.2 为什么 LSH 随机投影也称为“树”?
随机投影方法有时称为LSH 树。这是因为哈希码分配的过程可以用决策树的形式表示,其中每个节点包含向量是否位于当前超平面的负侧或正侧的条件。

第一个节点检查向量相对于红色超平面位于哪一侧。第二层的节点检查相同的条件,但相对于绿色超平面。最后,第三级检查蓝色超平面的相对位置。基于这 3 个条件,为向量分配一个 3 位哈希值。
三、超平面森林
超平面是随机构造的。这可能会导致如下图所示的数据集点分离不佳的情况。
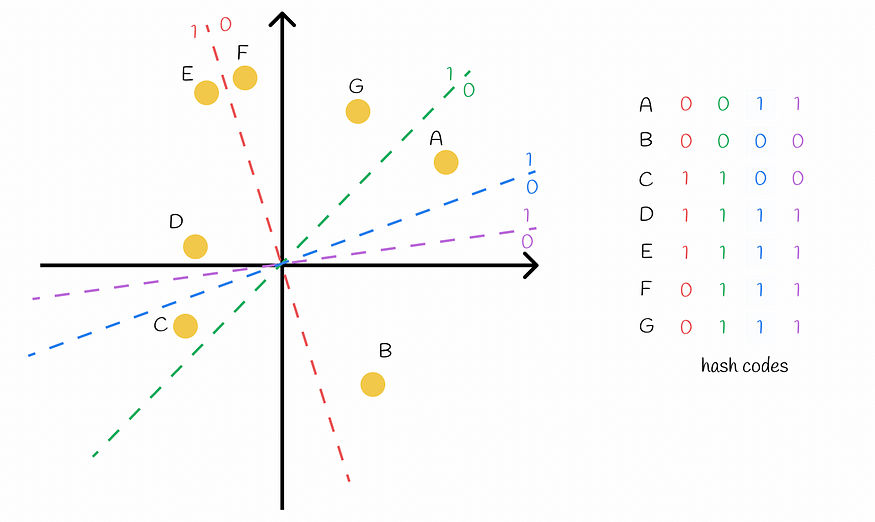
构造 4 个超平面以将数据集点表示为 4 长度的二进制向量。尽管 D 点和 E 点具有相同的哈希码,但它们彼此相距相对较远(FP)。相反的情况发生在一对位于不同区域但彼此非常接近的点 E 和 F (FN) 上。考虑到汉明距离,该算法通常预测 D 点比 F 点更接近 E。
从技术上讲,当两个点具有相同的哈希码但彼此相距很远时,这并不是什么大问题。在算法的下一步中,这些点将被作为候选点并进行充分比较——这样算法就可以消除误报情况。假阴性的情况更加复杂:当两个点具有不同的哈希码但实际上彼此接近时。
为什么不使用与经典机器学习中的决策树相同的方法,将其组合成随机森林来提高整体预测质量?如果一个估计器犯了错误,其他估计器可以产生更好的预测并减轻最终的预测误差。利用这个想法,构建随机超平面的过程可以独立重复。生成的哈希值可以聚合为一对向量,其方式与上一章中的 minhash 值类似:
如果查询与另一个向量至少有一次相同的哈希码,则它们被视为候选者。
使用这种机制可以减少假阴性的数量。
四、质量与速度的权衡
选择适当数量的超平面在数据集上运行非常重要。选择的超平面越多来划分数据集点,冲突就越少,计算哈希码所需的时间就越多,存储它们的内存也就越多。确切地说,如果一个数据集由n 个向量组成,并且我们将其分割为k 个超平面,那么平均每个可能的哈希码将被分配给n / 2ᵏ个向量。
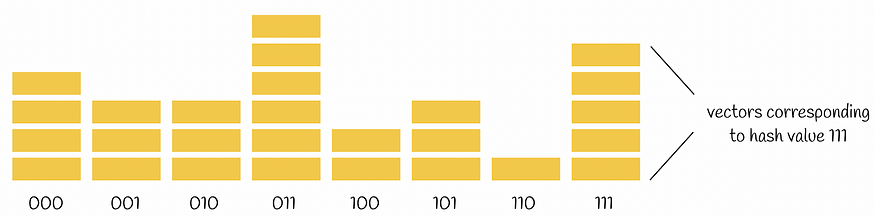
k = 3 产生 2³ = 8 个桶
五、复杂性研究
5.1 训练
LSH Forest 训练阶段由两部分组成:
- k 个超平面的生成。这是一个相对较快的过程,因为d维空间中的单个超平面可以在O(d)时间内生成。
- 为所有数据集向量分配哈希码。此步骤可能需要时间,尤其是对于大型数据集。获取单个哈希码需要O(dk)的时间。如果数据集由 n 个向量组成,则总复杂度变为O(ndk)。
对于森林中的每棵树,上述过程都会重复几次。

训练复杂性
5.2 推理
LSH 森林的优点之一是其快速推理,包括两个步骤:
- 获取查询的哈希码。这相当于计算k 个标量积,结果为O(dk)时间(d — 维数)。
- 通过计算到候选者的精确距离,在同一存储桶(具有相同哈希码的向量)中查找距查询最近的邻居。对于O(d) ,距离计算呈线性进行。每个桶平均包含n / 2ᵏ个向量。因此,计算到所有潜在候选者的距离需要O(dn / 2ᵏ)的时间。
总复杂度为O(dk + dn / 2ᵏ)。
像往常一样,对于森林中的每棵树,上述过程都会重复几次。

推理复杂度
当超平面k的数量选择为n ~ 2ᵏ(在大多数情况下是可能的)时,总推理复杂度变为O(ldk) (l是树的数量)。基本上,这意味着计算时间不取决于数据集大小!这种微妙之处导致了对数百万甚至数十亿向量的相似性搜索的有效可扩展性。
六、错误率
在有关 LSH 的文章的前一部分中,我们讨论了如何根据两个向量的签名相似性来确定两个向量被选为候选向量的概率。在这里,我们将使用几乎相同的逻辑来找到 LSH 森林的公式。

令 s 为两个向量在其哈希值的相同位置具有相同位的概率(稍后将估计 s)

两个向量的长度为 k 的哈希码相等的概率
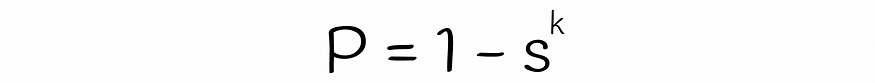
两个向量的长度为 k 的哈希码不同(或至少一位不同)的概率
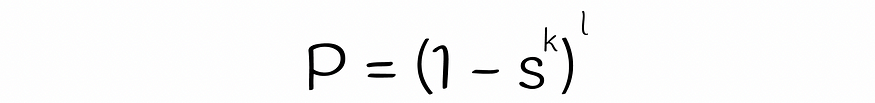
两个向量的所有 l 个哈希码(对于 l 个超平面)都不同的概率
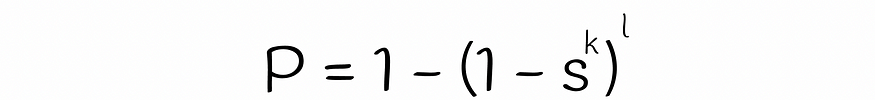
两个向量的 l 个哈希码中至少有一个相等的概率,因此向量将成为候选向量
到目前为止,我们几乎已经得到了估计两个向量成为候选向量的概率的公式。剩下的唯一事情就是估计方程中变量s的值。在经典的LSH算法中,s等于两个向量的Jaccard指数或签名相似度。另一方面,为了估计LSH 森林的s,将使用线性代数理论。
坦率地说,s是两个向量a和b具有相同位的概率。该概率相当于随机超平面将这些向量分离到同一侧的概率。让我们想象一下:

向量 a 和 b 由蓝色超平面分隔。绿色超平面没有将它们分开。
从图中可以清楚地看出,只有当向量a和b从向量 a 和 b 之间经过时,超平面才会将它们分成两个不同的边。这种概率q与向量之间的角度成正比,可以轻松计算:

随机超平面分隔两个向量的概率(即它们具有不同的位)

随机超平面不分离两个向量的概率(即,它们具有相同的位)
将这个方程代入之前获得的方程得出最终公式:
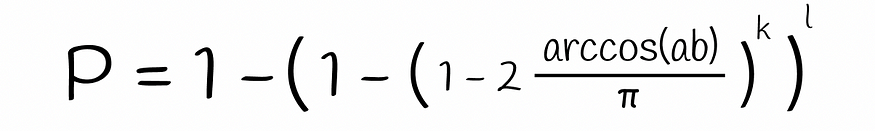
基于超平面数 k 和 LSH 树数 l 两个向量具有至少一个对应哈希值(即成为候选者)的概率
6.1 可视化
注意。余弦相似度正式定义在范围 [-1, 1] 中。为简单起见,我们将此区间映射到 [0, 1],其中 0 和 1 分别表示最低和最高可能的相似度。
利用最后获得的公式,让我们根据不同数量的超平面k和树l的余弦相似度来可视化两个向量作为候选向量的概率。

调整树的数量 l

调整超平面数量k
根据这些图,可以进行一些有用的观察:
- 余弦相似度为 1 的一对向量总是成为候选向量。
- 余弦相似度为 0 的一对向量永远不会成为候选向量。
- 当超平面k的数量减少或 LSH 树l的数量增加时,两个向量成为候选的概率P增加(即更多误报) 。相反的说法是正确的。
综上所述,LSH是一种非常灵活的算法:可以根据给定的问题调整不同的k和l值,得到满足问题要求的概率曲线。
6.2 例子
让我们看下面的例子。想象一下l = 5棵树是用k = 10 个超平面构建的。除此之外,还有两个向量的余弦相似度为0.8。在大多数系统中,这种余弦相似性表明向量确实彼此非常接近。根据前面几节的结果,这个概率只有 2.5%!显然,对于如此高的余弦相似度来说,这是一个非常低的结果。使用l = 5和k = 10这些参数会 导致大量漏报!下面的绿线代表这种情况下的概率。
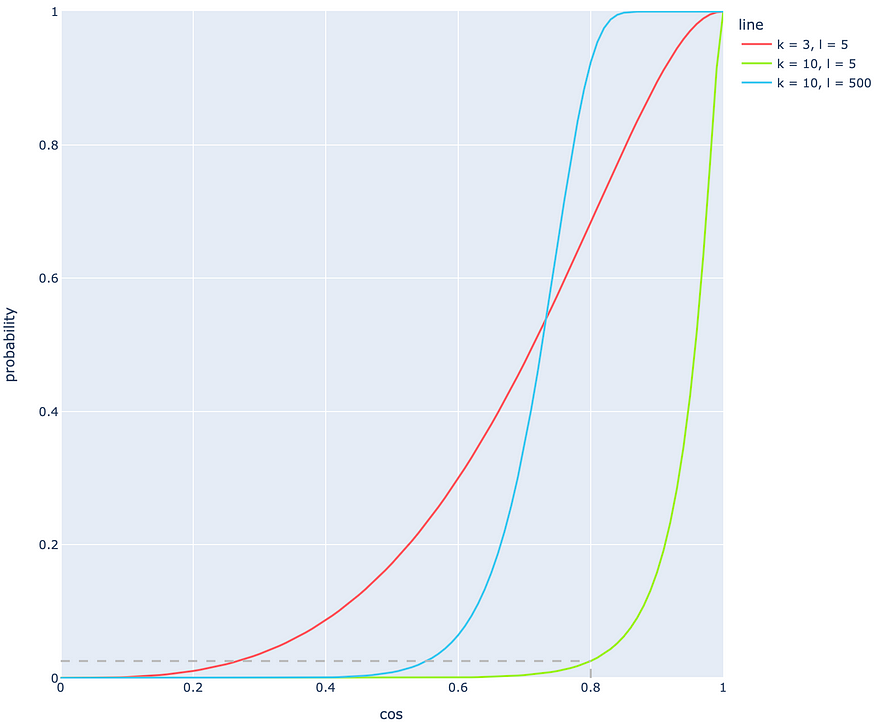
基于两个向量余弦相似度的概率曲线
这个问题可以通过调整k和l的更好值来将曲线向左移动来解决。
例如,如果k减小到 3(红线),则余弦相似度 0.8 的相同值将对应于 68% 的概率,这比以前更好。乍一看,红线似乎比绿线更适合,但请务必记住,使用较小的k值(如红线的情况)会导致大量碰撞。这就是为什么有时最好调整第二个参数,即树的数量l。
与k不同,它通常需要非常多的树l才能获得相似的线形状。在图中,蓝线是通过将l值从 10 更改为 500 从绿线获得的。蓝线显然比绿线拟合得更好,但仍远未达到完美:因为余弦之间的斜率很高。相似度值为0.6和0.8时,余弦相似度在0.3-0.5附近的概率几乎等于0,这是不利的。文档相似度为 0.3-0.5 的小概率在现实生活中通常应该更高。
根据最后一个例子,很明显,即使树的数量非常多(需要大量计算),仍然会导致许多漏报!这是随机投影方法的主要缺点:
尽管有可能获得完美的概率曲线,但它要么需要大量计算,要么会导致大量冲突。否则,会导致较高的假阴性率。
七、费斯实施
Faiss(Facebook AI Search Comparison)是一个用 C++ 编写的 Python 库,用于优化相似性搜索。该库提供了不同类型的索引,这些索引是用于有效存储数据和执行查询的数据结构。
根据Faiss文档中的信息,我们将了解如何构建LSH索引。
随机投影算法在 Faiss 中的IndexLSH类中实现。尽管 Faiss 作者使用了另一种称为“随机旋转”的技术,但它仍然与本文中描述的技术有相似之处。该类仅实现一个 LSH 树。如果我们想使用 LSH 森林,那么只需创建几个 LSH 树并聚合它们的结果就足够了。
IndexLSH类的构造函数有两个参数:
- d:维数
- nbits:编码单个向量所需的位数(可能的桶数等于2ⁿᵇᶦᵗˢ)
search() 方法返回的距离是到查询向量的汉明距离。

IndexLSH 的 Faiss 实现
此外,Faiss 允许通过调用faiss.vector_to_array(index.codes)方法检查每个数据集向量的编码哈希值。
由于每个数据集向量均由nbits二进制值编码,因此存储单个向量所需的字节数等于:
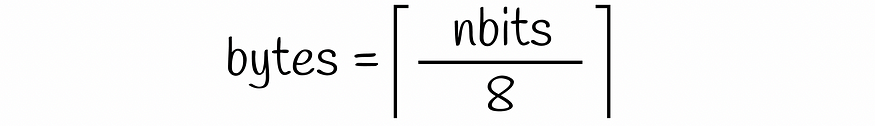
八、约翰逊-林登斯特劳斯引理
约翰逊-林登斯特劳斯引理是一个与降维相关的神话引理。虽然可能很难完全理解其原始陈述,但可以用简单的语言表述:
选择随机子集并将原始数据投影到其上可以保留点之间相应的成对距离。
更准确地说,拥有n 个点的数据集,可以在O(logn)维的新空间中表示它们,从而几乎保留点之间的相对距离。如果向量在 LSH 方法中由~logn二进制值编码,则可以应用引理。此外,LSH 完全按照引理要求以随机方式创建超平面。
Johnson-Lindenstrauss 引理的另一个令人难以置信的事实是,新数据集的维数不依赖于原始数据集的维数!实际上,这个引理对于非常小的维度来说效果不佳。
九、结论
我们已经使用了强大的相似性搜索算法。基于通过随机超平面分离点的简单想法,它通常在大型数据集上表现良好并且可扩展。此外,它具有良好的灵活性,允许选择适当数量的超平面和树。
Johnson-Lindenstrauss 引理的理论结果强化了随机预测方法的使用。
资源
维亚切斯拉夫·埃菲莫夫


![2023年中国有创呼吸机产量、需求量及行业市场规模分析[图]](https://img-blog.csdnimg.cn/img_convert/96ed74d0f2764f882efdcacf8a0b49e9.png)
![2023年中国热电厂发电装机量、热电厂发电量及市场需求分析[图]](https://img-blog.csdnimg.cn/img_convert/4f934f796f480e61848591ee361ec179.png)
![2023年中国液晶显示板产量、需求量、市场规模及价格趋势分析[图]](https://img-blog.csdnimg.cn/img_convert/2fa64e9e07355186e234baab42de42cd.png)