文章目录
- 代码
- 目录结构
- Vector.py
- _globals.py
- main_vector.py
- main_numpy_vector.py
- 一、创建属于自己的向量
- 1.1 在控制台测试__repr__和__str__方法
- 1.2 创建实例测试代码
- 二、向量的基本运算
- 2.1 加法
- 2.2 数量乘法
- 2.3 向量运算的基本性质
- 2.4 零向量
- 2.5 向量的长度
- 2.6 单位向量
- 2.7 点乘/内积:两个向量的乘法 --答案是一个标量
代码
目录结构
F:.
| main_numpy_vector.py
| main_vector.py
|
+---.idea
|
\---playLA
| Vector.py
| _globals.py
| __init__.py
|
\---__pycache__
Vector.py
import math
from ._globals import EPSILON
class Vector:
def __init__(self, lst):
"""
__init__ 代表类的构造函数
双下划线开头的变量 例如_values,代表类的私有成员
lst是个引用,list(lst)将值复制一遍,防止用户修改值
"""
self._values = list(lst)
def dot(self, another):
"""向量点乘,返回结果标量"""
assert len(self) == len(another), \
"Error in dot product. Length of vectors must be same."
return sum(a * b for a, b in zip(self, another))
def norm(self):
"""返回向量的模"""
return math.sqrt(sum(e**2 for e in self))
def normalize(self):
"""
归一化,规范化
返回向量的单位向量
此处设计到了除法: def __truediv__(self, k):
"""
if self.norm() < EPSILON:
raise ZeroDivisionError("Normalize error! norm is zero.")
return Vector(self._values) / self.norm()
# return 1 / self.norm() * Vector(self._values)
# return Vector([e / self.norm() for e in self])
def __truediv__(self, k):
"""返回数量除法的结果向量:self / k"""
return (1 / k) * self
@classmethod
def zero(cls, dim):
"""返回一个dim维的零向量
@classmethod 修饰符对应的函数不需要实例化,不需要 self 参数,但第一个参数需要是表示自身类的cls参数,可以来调用类的属性,类的方法,实例化对象等。
"""
return cls([0] * dim)
def __add__(self, another):
"""向量加法,返回结果向量"""
assert len(self) == len(another), \
"Error in adding. Length of vectors must be same."
# return Vector([a + b for a, b in zip(self._values, another._values)])
return Vector([a + b for a, b in zip(self, another)])
def __sub__(self, another):
"""向量减法,返回结果向量"""
assert len(self) == len(another), \
"Error in subtracting. Length of vectors must be same."
return Vector([a - b for a, b in zip(self, another)])
def __mul__(self, k):
"""返回数量乘法的结果向量:self * k"""
return Vector([k * e for e in self])
def __rmul__(self, k):
"""
返回数量乘法的结果向量:k * self
self本身就是一个列表
"""
return self * k
def __pos__(self):
"""返回向量取正的结果向量"""
return 1 * self
def __neg__(self):
"""返回向量取负的结果向量"""
return -1 * self
def __iter__(self):
"""返回向量的迭代器"""
return self._values.__iter__()
def __getitem__(self, index):
"""取向量的第index个元素"""
return self._values[index]
def __len__(self):
"""返回向量长度(有多少个元素)"""
return len(self._values)
def __repr__(self):
"""打印显示:Vector([5, 2])"""
return "Vector({})".format(self._values)
def __str__(self):
"""打印显示:(5, 2)"""
return "({})".format(", ".join(str(e) for e in self._values))
_globals.py
# 包中的变量,但是对包外不可见,因此使用“_”开头
EPSILON = 1e-8
main_vector.py
from playLA.Vector import Vector
if __name__ == "__main__":
vec = Vector([5, 2])
print(vec)
print("len(vec) = {}".format(len(vec)))
print("vec[0] = {}, vec[1] = {}".format(vec[0], vec[1]))
vec2 = Vector([3, 1])
print("{} + {} = {}".format(vec, vec2, vec + vec2))
print("{} - {} = {}".format(vec, vec2, vec - vec2))
print("{} * {} = {}".format(vec, 3, vec * 3))
print("{} * {} = {}".format(3, vec, 3 * vec))
print("+{} = {}".format(vec, +vec))
print("-{} = {}".format(vec, -vec))
zero2 = Vector.zero(2)
print(zero2)
print("{} + {} = {}".format(vec, zero2, vec + zero2))
print("norm({}) = {}".format(vec, vec.norm()))
print("norm({}) = {}".format(vec2, vec2.norm()))
print("norm({}) = {}".format(zero2, zero2.norm()))
print("normalize {} is {}".format(vec, vec.normalize()))
print(vec.normalize().norm())
print("normalize {} is {}".format(vec2, vec2.normalize()))
print(vec2.normalize().norm())
try:
zero2.normalize()
except ZeroDivisionError:
print("Cannot normalize zero vector {}.".format(zero2))
print("========点乘:========")
print(vec.dot(vec2))
main_numpy_vector.py
import numpy as np
if __name__ == "__main__":
print(np.__version__)
# np.array 基础
print("========np.array 基础========")
lst = [1, 2, 3]
lst[0] = "Linear Algebra"
print(lst)
print("========vec = np.array([1, 2, 3])========")
vec = np.array([1, 2, 3])
print(vec)
# vec[0] = "Linear Algebra"
# vec[0] = 666
# print(vec)
print("========np.array的创建========")
# np.array的创建
print(np.zeros(5))
print(np.ones(5))
print(np.full(5, 666))
print("========np.array的基本属性========")
# np.array的基本属性
print(vec)
print("size =", vec.size)
print("size =", len(vec))
print(vec[0])
print(vec[-1])
print(vec[0: 2])
print(type(vec[0: 2]))
print("========np.array的基本运算========")
# np.array的基本运算
vec2 = np.array([4, 5, 6])
print("{} + {} = {}".format(vec, vec2, vec + vec2))
print("{} - {} = {}".format(vec, vec2, vec - vec2))
print("{} * {} = {}".format(2, vec, 2 * vec))
print("没有数学意义的乘法:{} * {} = {}".format(vec, vec2, vec * vec2))
print("{}.dot({}) = {}".format(vec, vec2, vec.dot(vec2)))
print("========求模========")
print(np.linalg.norm(vec))
print("========归一化========")
print(vec / np.linalg.norm(vec))
print("========单位向量========")
print(np.linalg.norm(vec / np.linalg.norm(vec)))
print("========零向量会报错========")
zero3 = np.zeros(3)
print(zero3 / np.linalg.norm(zero3))
一、创建属于自己的向量
class Vector:
def __init__(self, lst):
self._values = lst
def __getitem__(self, index):
"""取向量的第index个元素"""
return self._values[index]
def __len__(self):
"""返回向量长度(有多少个元素)"""
return len(self._values)
def __repr__(self):
"""打印显示:Vector([5, 2])"""
return "Vector({})".format(self._values)
def __str__(self):
"""打印显示:(5, 2)"""
return "({})".format(", ".join(str(e) for e in self._values))
1.1 在控制台测试__repr__和__str__方法
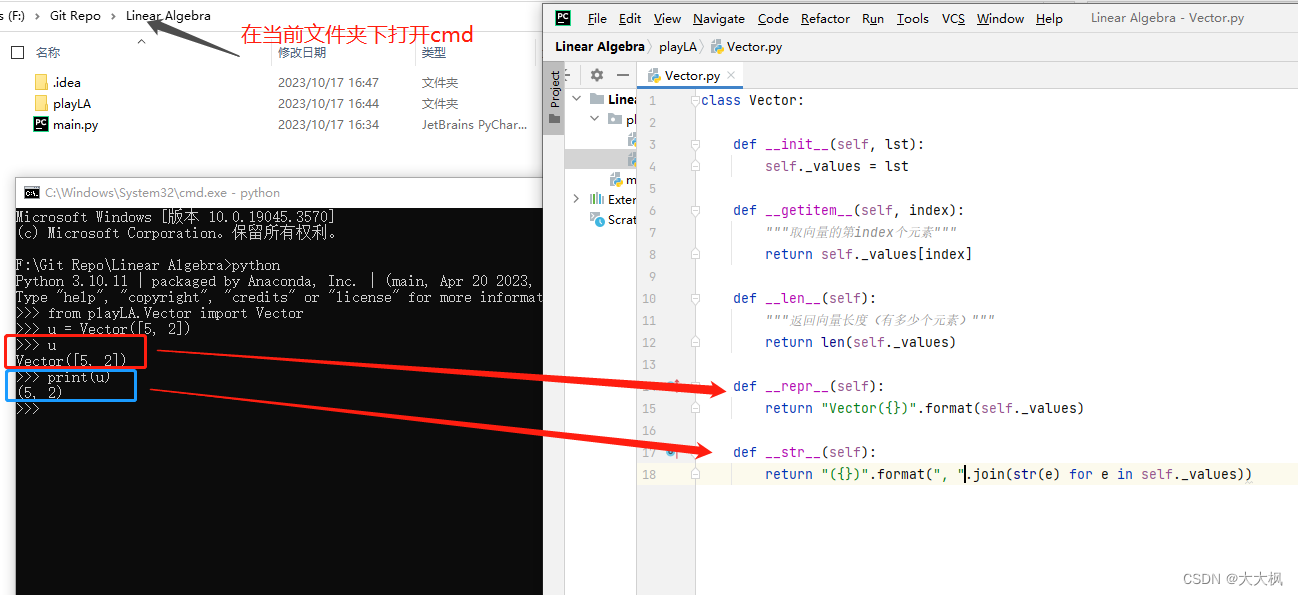
1.2 创建实例测试代码
from playLA.Vector import Vector
if __name__ == "__main__":
vec = Vector([5, 2])
print(vec)
print("len(vec) = {}".format(len(vec)))
print("vec[0] = {}, vec[1] = {}".format(vec[0], vec[1]))
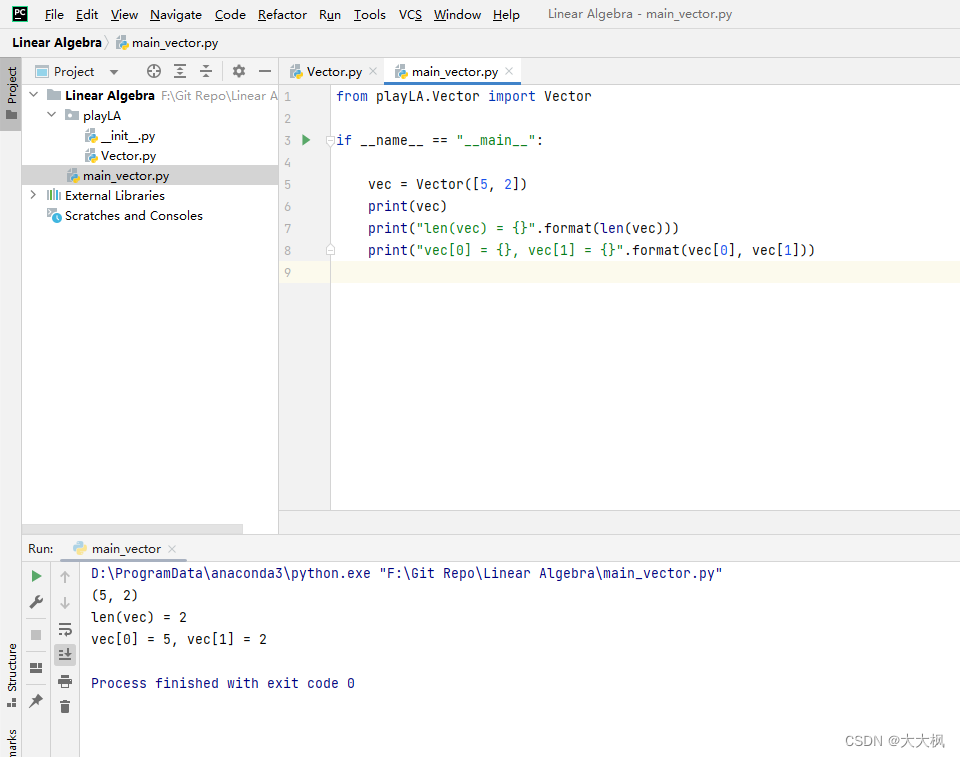
二、向量的基本运算
2.1 加法

2.2 数量乘法

2.3 向量运算的基本性质

2.4 零向量




2.5 向量的长度


2.6 单位向量
单位向量叫做 u hat
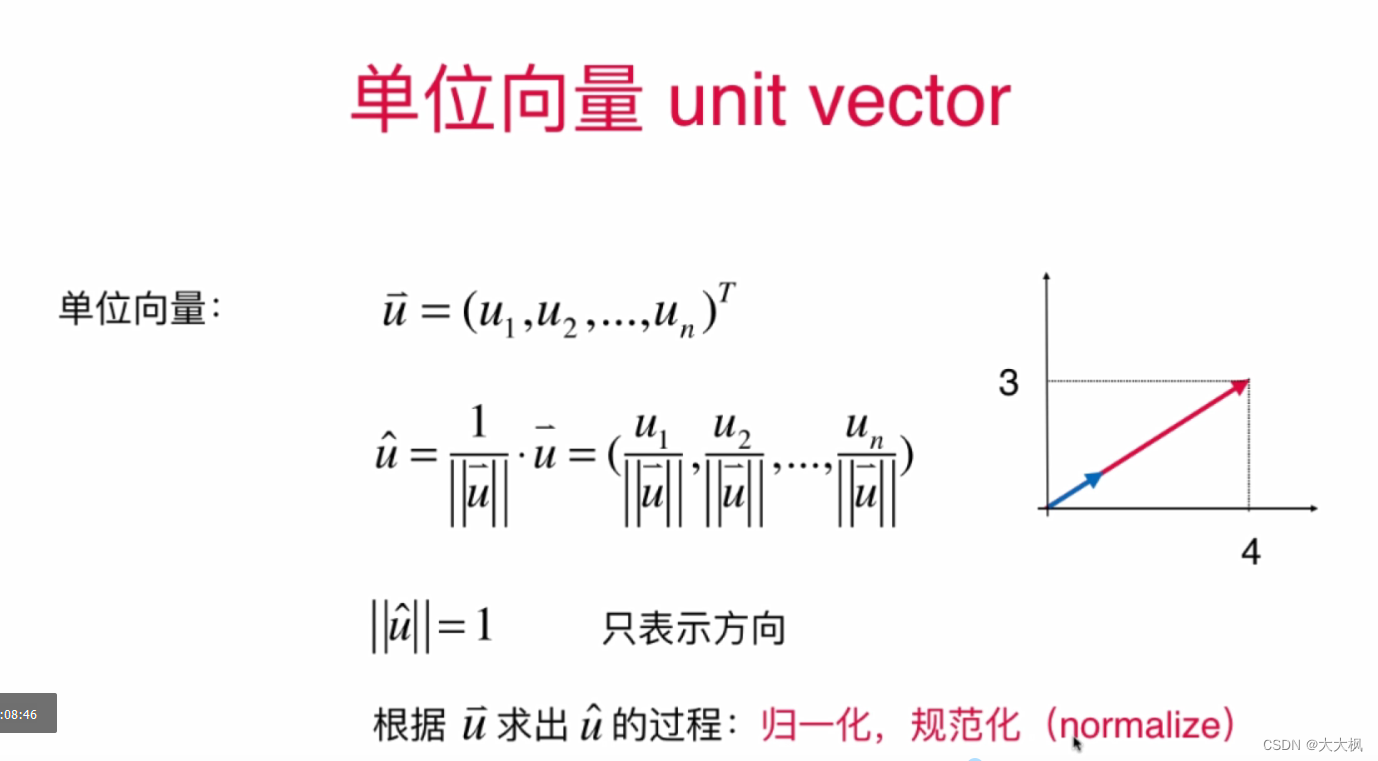

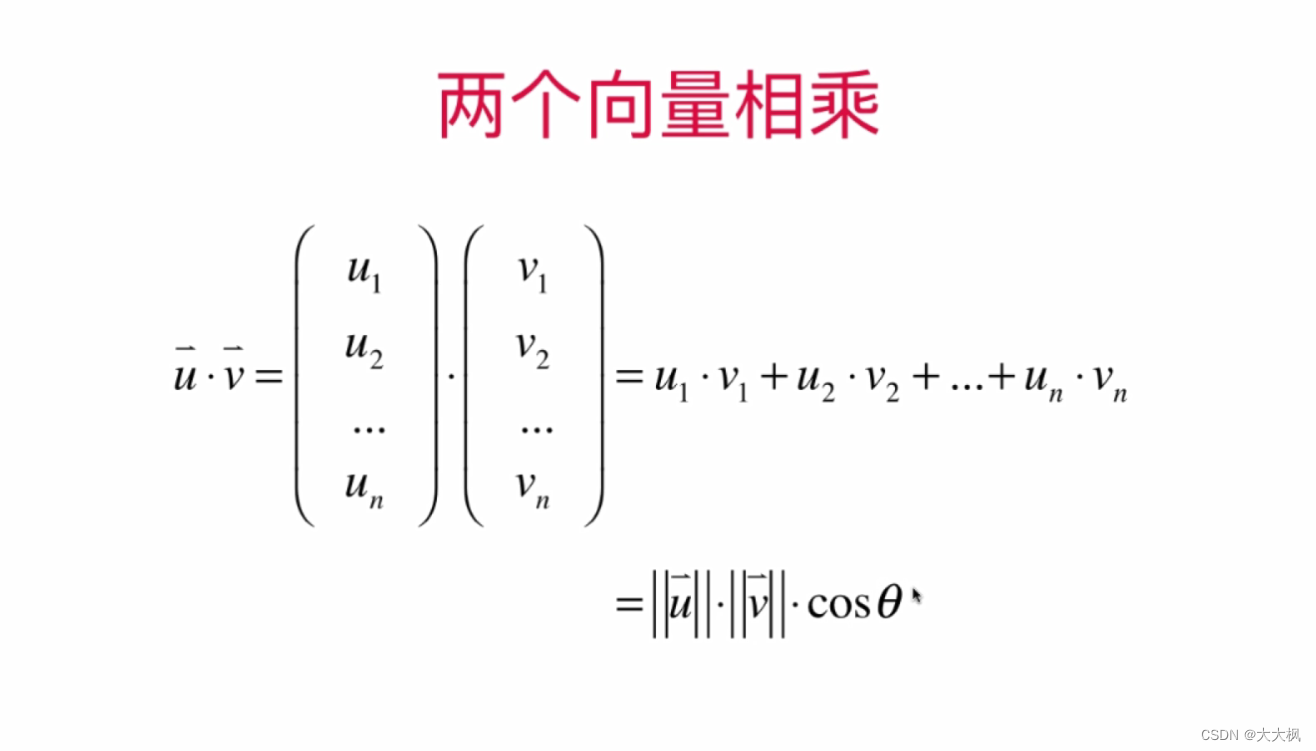
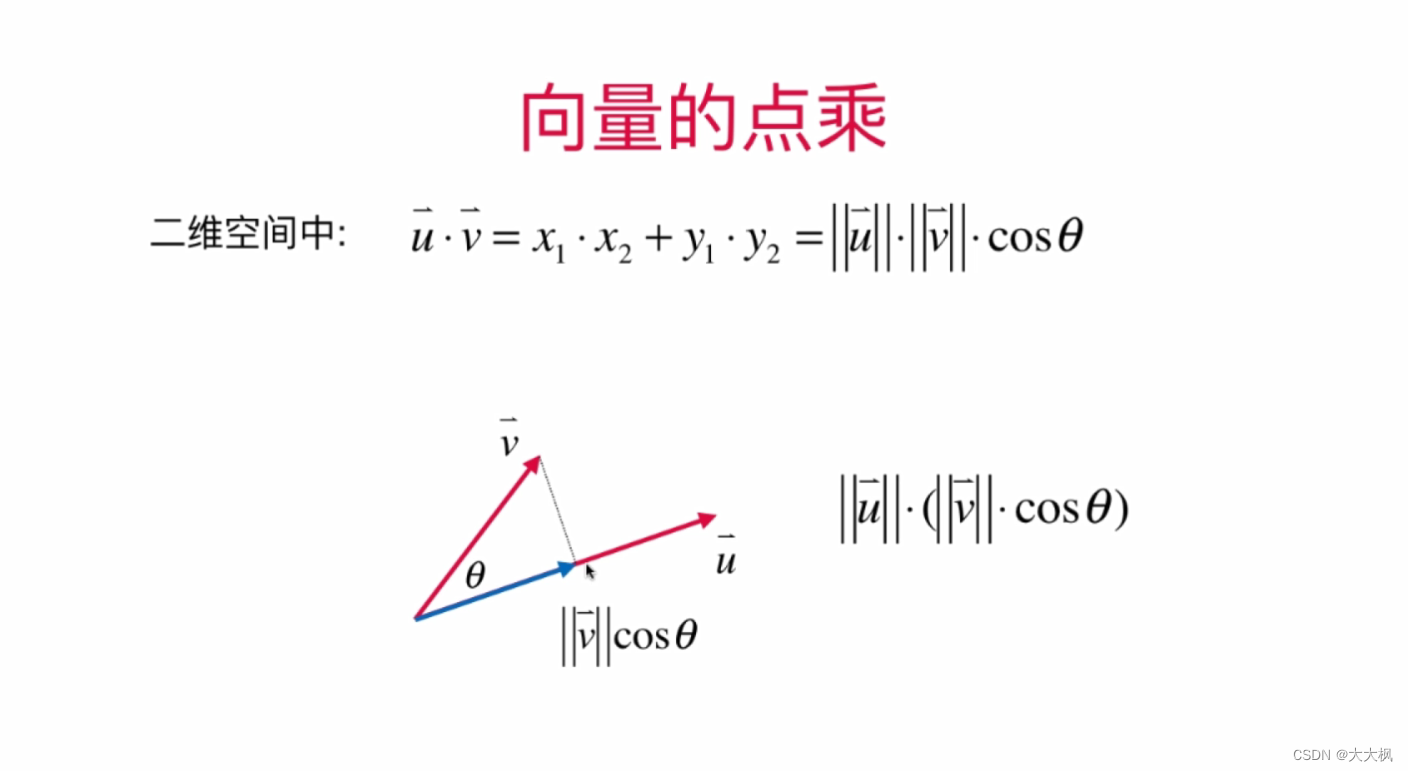
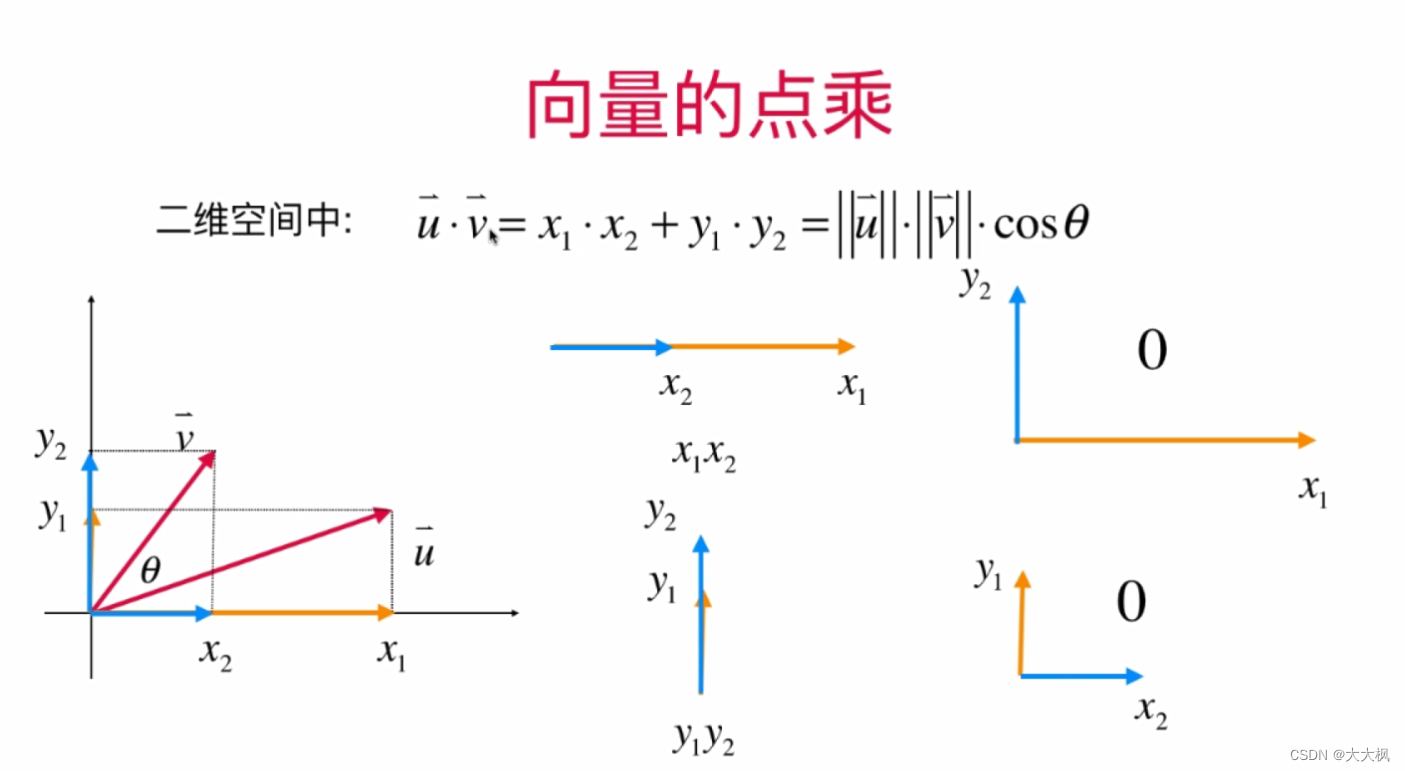
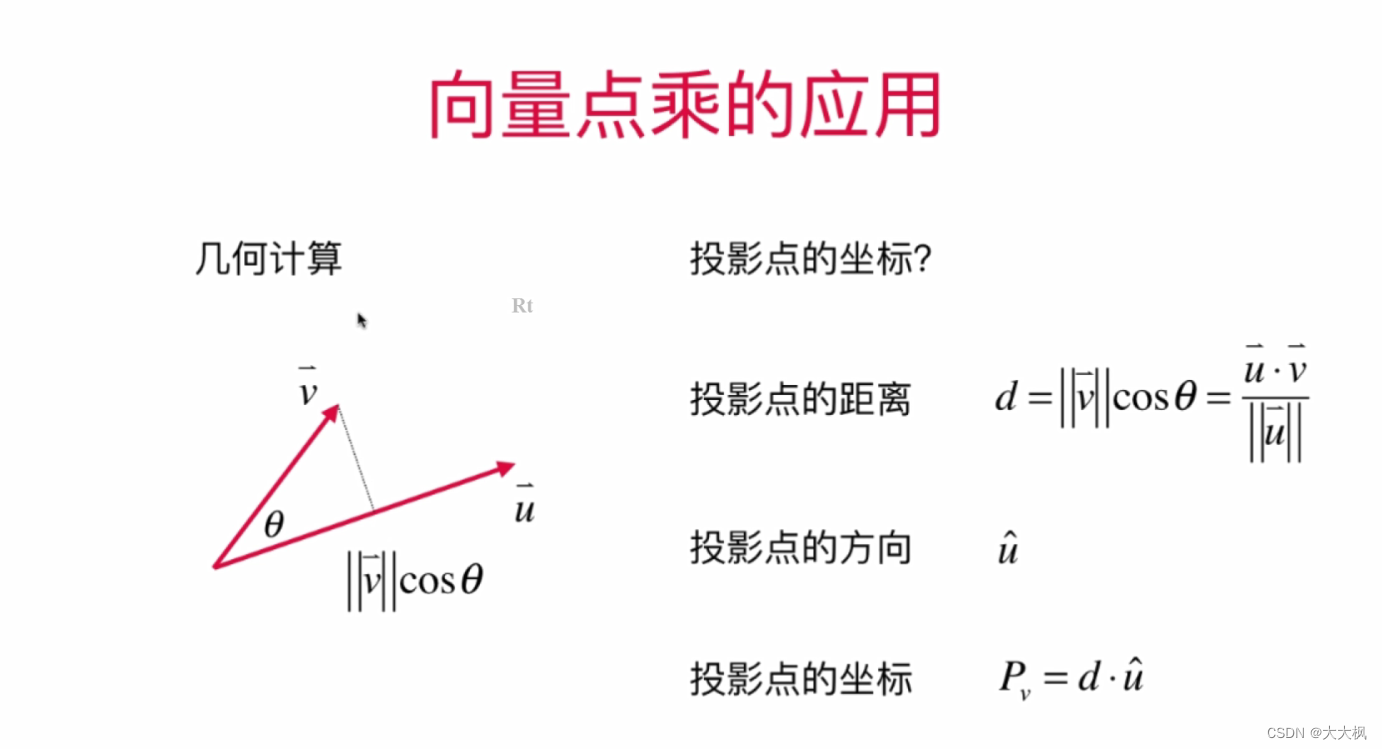
2.7 点乘/内积:两个向量的乘法 --答案是一个标量










![聊聊分布式架构07-[Spring]IoC和AOP](https://img-blog.csdnimg.cn/70f677592e714c87875a653bab6bf9e6.png)