互异数

news2024/11/20 22:42:47

这道题是实验舱举办的"编程一小时"千人马拉松竞赛的第三题!

#C、互异数

题目描述

输入格式

输出格式

输入样例1

输出样例1

输入样例2

输出样例2

数据规模

思路:

1.最大互质数

2.互质数的数量

3.贪心策略

总代码:

总结:

题目链接:

#C、互异数

题目描述

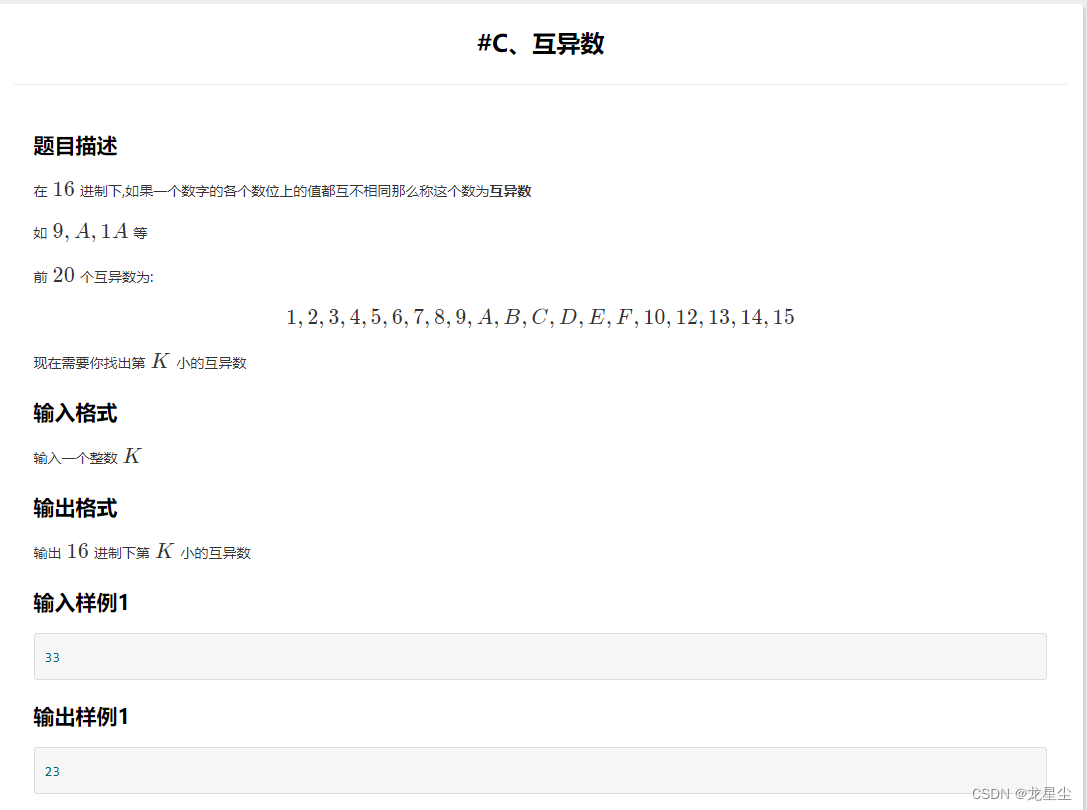
在1616进制下,如果一个数字的各个数位上的值都互不相同那么称这个数为互异数

如9,A,1A9,A,1A等

前2020个互异数为:

1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,12,13,14,151,2,3,4,5,6,7,8,9,A,B,C,D,E,F,10,12,13,14,15

现在需要你找出第KK小的互异数

输入格式

输入一个整数KK

输出格式

输出1616进制下第KK小的互异数

输入样例1

33

输出样例1

23

输入样例2

546481140

输出样例2

FEDCBA98

数据规模

对于30\%30%的数据,1 \leq K \leq 10^31≤K≤103
对于70\%70%的数据,1 \leq K \leq 10^71≤K≤107
对于100\%100%的数据,1 \leq K \leq 533194120811401≤K≤53319412081140

思路:

1.最大互质数

不难想到

最大的互异数为FEDCBA9876543210

2.互质数的数量

长度为 lenlen 的互异数有 15 \times A_{15}^{len-1}15×A15len−1 个

一共有 \displaystyle \sum_{i=1}^{16} 15 \times A_{15}^{i-1} = 53319412081140i=1∑1615×A15i−1=53319412081140 个互异数

求第KK小较为不易

3.贪心策略

确定第 KK 小互异数的长度 lenlen,不妨转化为求长度为 lenlen 的第 SS 大

从高到低逐数位贪心考虑填入\text{0} \sim \text{F}0∼F,每个数位从 \text{F} \rightarrow \text{0}F→0 尝试放入(首位忽略00,已放过的值不再考虑)

设当前从高到低考虑到第 pp 个数位,当前尝试的数位值为 c_pcp

若当前数位已确定,那么 p+1 \sim lenp+1∼len 数位构成的互异数有A_{16-p}^{len-p}A16−plen−p个

若S \gt A_{16-p}^{len-p}S>A16−plen−p

说明此时c_pcp贡献排名不够尝试更小的数位

同时令 S\leftarrow S - A_{16-p}^{len-p}S←S−A16−plen−p

若此时 S \leq A_{16-p}^{len-p}S≤A16−plen−p

说明此时c_pcp贡献排名足够,当前数位值已经确定为c_pcp,继续考虑下一个数位

总代码:

#include <bits/stdc++.h>
using namespace std;
long long k, fac[21], len = 16, cnt[21], b[21], T = 53319412081140;
bool vis[21];
char str[] = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'};
long long A(int n, int m)
{
  if (m > n)
    return 0;
  return fac[n] / fac[n - m];
}
int main()
{
  #endif
  fac[0] = fac[1] = 1;
  for (int i = 2; i <= 21; i++)
    fac[i] = fac[i - 1] * i;
  scanf("%lld", &k);
  for (int i = 16; i; i--)
    cnt[i] = cnt[i + 1] + 15 * A(15, i - 1); //求出各数位的互异数个数,求出前缀和
  k = T - k + 1; //转成全局第 S 大
  while (k > cnt[len]) //确定位数
    len--;
  k -= cnt[len + 1]; //转为长度为 len 的第 S 大
  for (int i = 1; i <= len; i++) //逐数位考虑
    for (int j = 15; j >= (i == len ? 1 : 0); j--)
    {
      if (vis[j])
        continue;
      long long x = A(16 - i, len - i);
      if (k > x)
        k -= x;
      else
      {
        vis[j] = true, putchar(str[j]);
        break;
      }
    }
  return 0;
}