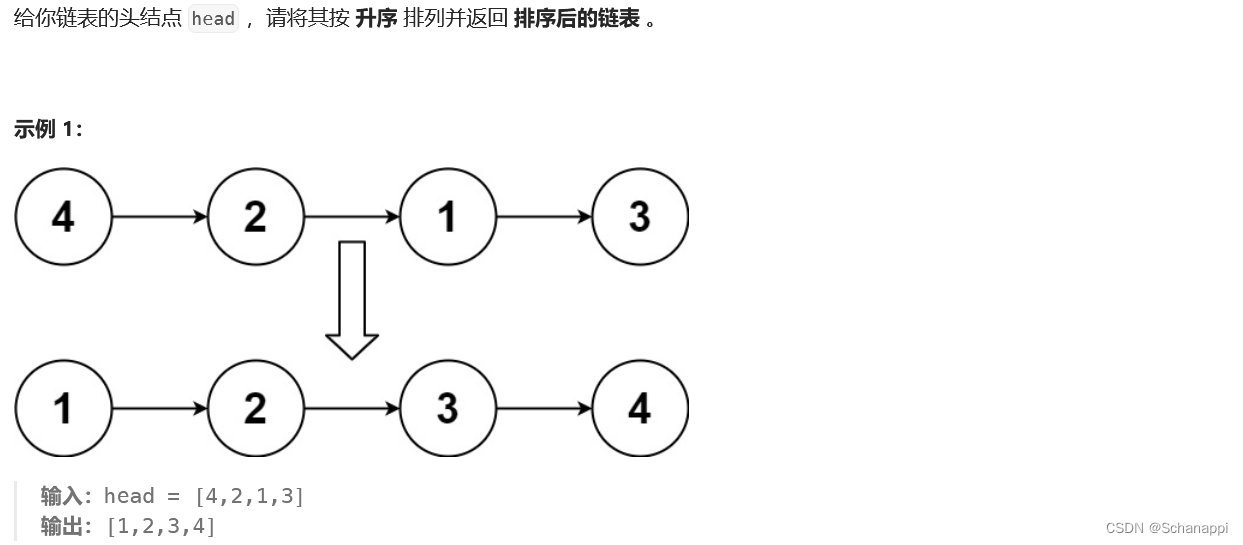
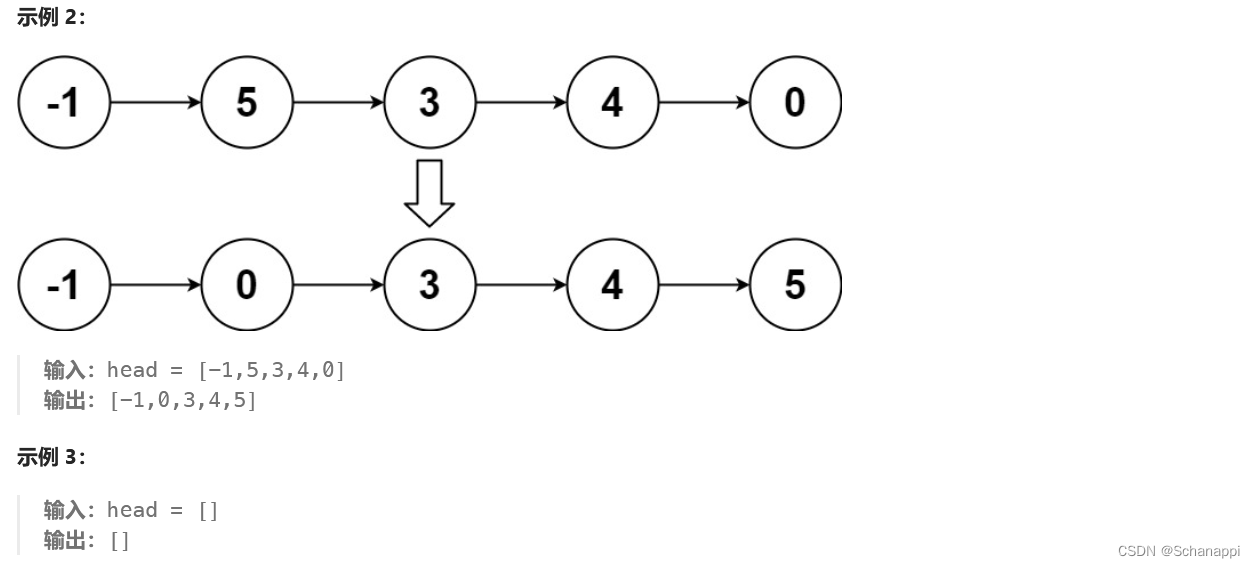
148. 排序链表(中等)

方法一:归并排序(递归法)
思路
-
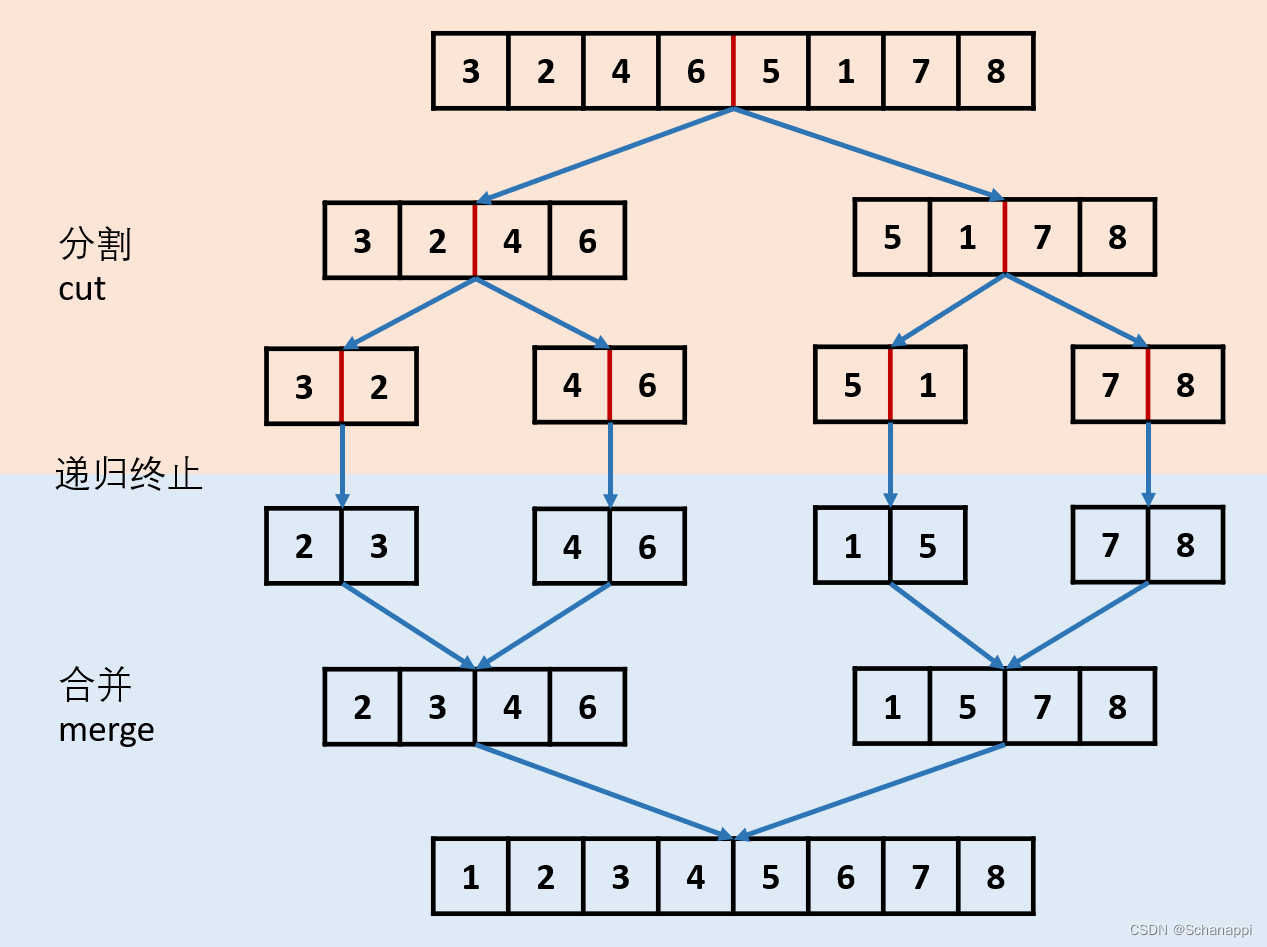
题目要求时间空间复杂度分别为 O(nlogn) 和 O(1) ,根据时间复杂度我们自然想到二分法,从而联想到归并排序;
-
对数组做归并排序的空间复杂度为 O(n) ,分别由新开辟数组 O(n) 和递归函数调用 O(logn) 组成,而根据链表特性:
- 数组额外空间:链表可以通过修改引用来更改节点顺序,无需像数组一样开辟额外空间;
- 递归额外空间:递归调用函数将带来 O(logn) 的空间复杂度,因此若希望达到 O(1) 空间复杂度,则不能使用递归。
-
通过递归实现链表归并排序,有以下两个环节:
- 分割 cut 环节: 找到当前链表 中点,并从中点将链表断开(以便在下次递归 cut 时,链表片段拥有正确边界);
- 我们使用
fast,slow快慢双指针法,「奇数个节点找到中点,偶数个节点找到中心左边的节点」。 - 找到中点
slow后,执行slow->next = nullptr;将链表切断。 - 递归分割时,输入当前链表左端点
head和中心节点slow的下一个节点tmp(因为链表是从 slow 切断的)。 - cut 递归终止条件: 当
head->next == nullptr时,说明只有一个节点了,直接返回此节点。
- 我们使用
- 合并 merge 环节: 将两个排序链表合并,转化为一个排序链表。
- 双指针法合并,建立辅助
ListNode* h作为头部。 - 设置两指针
left, right分别指向两链表头部,比较两指针处节点值大小,由小到大加入合并链表头部,指针交替前进,直至添加完两个链表。
返回辅助ListNode* h作为头部的下个节点h->next。 - 时间复杂度 O(l + r),l, r 分别代表两个链表长度。
- 双指针法合并,建立辅助
- 当题目输入的
head == nullptr时,直接返回 None。
- 分割 cut 环节: 找到当前链表 中点,并从中点将链表断开(以便在下次递归 cut 时,链表片段拥有正确边界);
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == nullptr || head->next == nullptr) {
return head;
}
// 定义快慢指针找到分割中点 slow
ListNode* fast = head->next;
ListNode* slow = head;
while(fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
// 右半边的头节点 tmp
ListNode* tmp = slow->next;
// 左右分割
slow->next = nullptr;
// 递归分割
ListNode* left = sortList(head);
ListNode* right = sortList(tmp);
// 定义辅助头节点 h
ListNode* h = new ListNode(0);
ListNode* res = h; // res保存h的头节点
// 合并
while (left && right) {
if (left->val < right->val) {
h->next = left;
left = left->next;
}
else {
h->next = right;
right = right->next;
}
h = h->next;
}
// 检查是left为空还是right为空
h->next = left != nullptr ? left : right;
return res->next;
}
};
方法二:归并排序(从底至顶直接合并)
思路
-
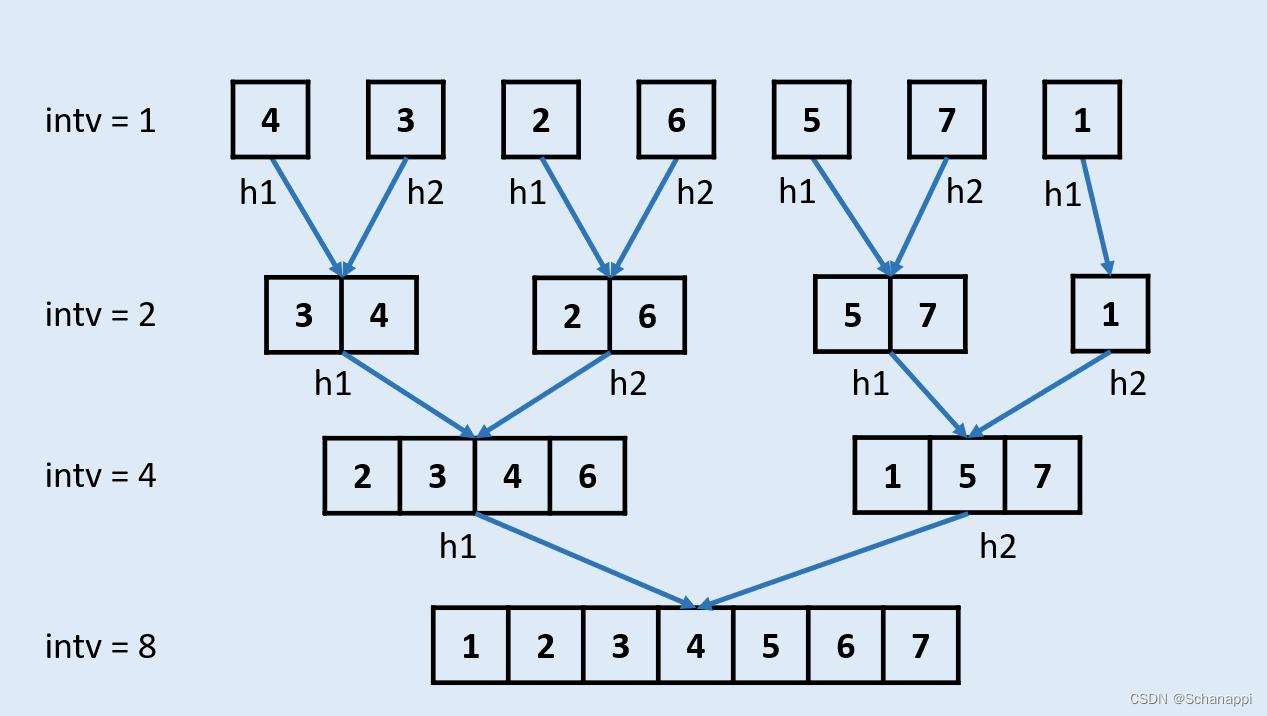
对于非递归的归并排序,需要使用迭代的方式替换 cut 环节:
- cut 环节本质上是通过二分法得到链表最小节点单元,再通过多轮合并得到排序结果。
- 每一轮合并 merge 操作针对的单元都有固定长度 intv,例如:
- 第一轮合并时 intv = 1,即将整个链表切分为多个长度为 1 的单元,并按顺序两两排序合并,合并完成的已排序单元长度为 2。
- 第二轮合并时 intv = 2,即将整个链表切分为多个长度为 2 的单元,并按顺序两两排序合并,合并完成已排序单元长度为 4。
- 以此类推,直到单元长度 intv >= 链表长度,代表已经排序完成。
- 根据以上推论,我们可以仅根据 intv 计算每个单元边界,并完成链表的每轮排序合并,例如:
- 当 intv = 1 时,将链表第 1 和第 2 节点排序合并,第 3 和第 4 节点排序合并,……。
- 当 intv = 2 时,将链表第 1-2 和第 3-4 节点排序合并,第 5-6 和第 7-8 节点排序合并,……。
- 当 intv = 4 时,将链表第 1-4 和第 5-8 节点排序合并,第 9-12 和第 13-16 节点排序合并,……。
-
此方法时间复杂度 O(nlogn) ,空间复杂度 O(1) 。
-
模拟上述的多轮排序合并:
- 统计链表长度 length,用于通过判断 intv < length 判定是否完成排序;
- 额外声明一个节点 res,作为头部后面接整个链表,用于:
- intv *= 2 即切换到下一轮合并时,可通过 res->next 找到链表头部 h;
- 执行排序合并时,需要一个辅助节点作为头部,而 res 则作为链表头部排序合并时的辅助头部 pre;后面的合并排序可以将上次合并排序的尾部 tail 用做辅助节点。
- 在每轮 intv 下的合并流程:
- 根据 intv 找到合并单元 1 和单元 2 的头部 h1, h2。由于链表长度可能不是 2^n,需要考虑边界条件:
- 在找 h2 过程中,如果链表剩余元素个数少于 intv,则无需合并环节,直接 break,执行下一轮合并;
- 若 h2 存在,但以 h2 为头部的剩余元素个数少于 intv,也执行合并环节,h2 单元的长度为 c2 = intv - i。
- 合并长度为 c1, c2 的 h1, h2 链表,其中:
- 合并完后,需要修改新的合并单元的尾部 pre 指针指向下一个合并单元头部 h。(在寻找 h1, h2 环节中,h指针已经被移动到下一个单元头部)
- 合并单元尾部同时也作为下次合并的辅助头部 pre。
- 当 h == None,代表此轮 intv 合并完成,跳出。
- 根据 intv 找到合并单元 1 和单元 2 的头部 h1, h2。由于链表长度可能不是 2^n,需要考虑边界条件:
- 每轮合并完成后将单元长度 ×2,切换到下轮合并:intv *= 2。
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == nullptr || head->next == nullptr) return head;
int intv = 1, length = 0;
// res保存已排序的结果链表头节点
ListNode* res = new ListNode(0);
res->next = head;
// pre指向已排序的结果链表的末尾
// h指向待排序链表的头节点
ListNode* pre;
ListNode* h;
// 遍历链表,得到长度
while (head) {
length ++;
head = head->next;
}
while (intv < length) {
pre = res;
h = res->next;
// 当待排序链表头节点不为空,说明还需要归并
while(h) {
// tmp1保存合并单元1的头节点
ListNode* tmp1 = h;
int len1 = intv;
while (len1 > 0 && h) {
len1 --;
h = h->next;
}
if(len1 > 0) {
break;
}
// tmp2保存合并单元2的头节点
ListNode* tmp2 = h;
int len2 = intv;
while (len2 > 0 && h) {
len2 --;
h = h->next;
}
// c1 c2分别是合并单元剩余的节点(即合并单元各自的节点数)
int c1 = intv, c2 = intv - len2;
while (c1 > 0 && c2 > 0) {
if (tmp1->val > tmp2->val) {
pre->next = tmp2;
tmp2 = tmp2->next;
c2 --; // 减少一个节点
}
else {
pre->next = tmp1;
tmp1 = tmp1->next;
c1--;
}
pre = pre->next;
}
// 将c1剩余节点连接到已排序节点的末尾
if(c1 > 0) {
pre->next = tmp1;
}
else {
pre->next = tmp2;
}
// 更新pre 使其指向已排序链表的末尾
while (c1-- > 0 || c2-- > 0) {
pre = pre->next;
}
// 将已排序链表和待排序链表连接
pre->next = h;
}
intv *= 2;
}
return res->next;
}
};
参考资料
- Sort List (归并排序链表)