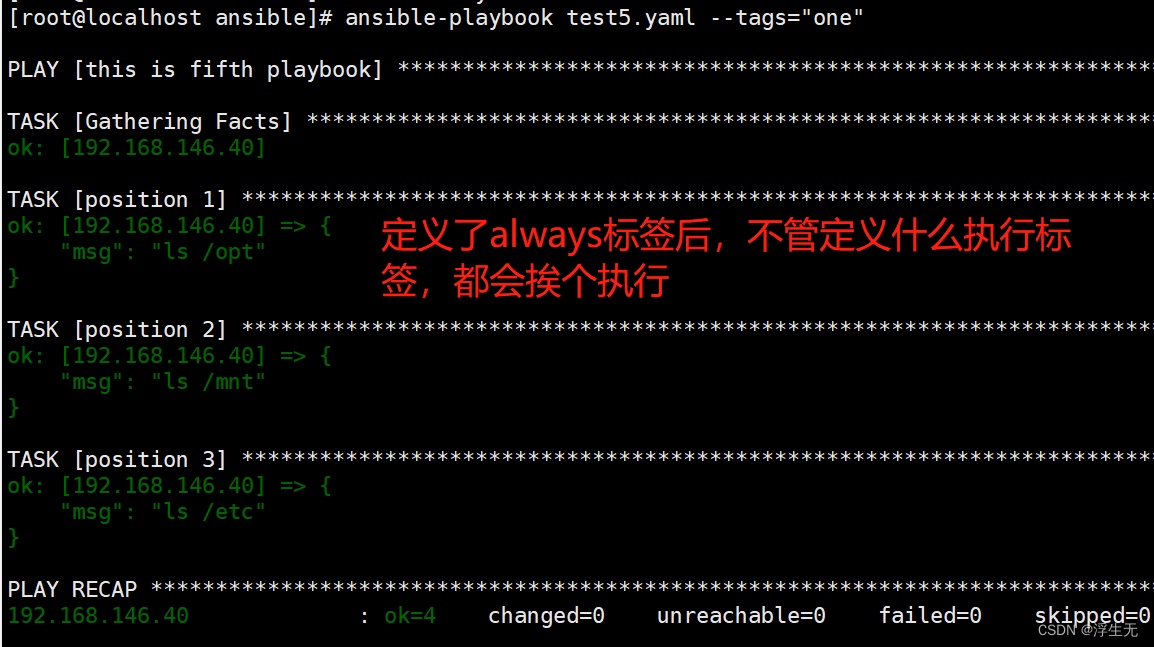
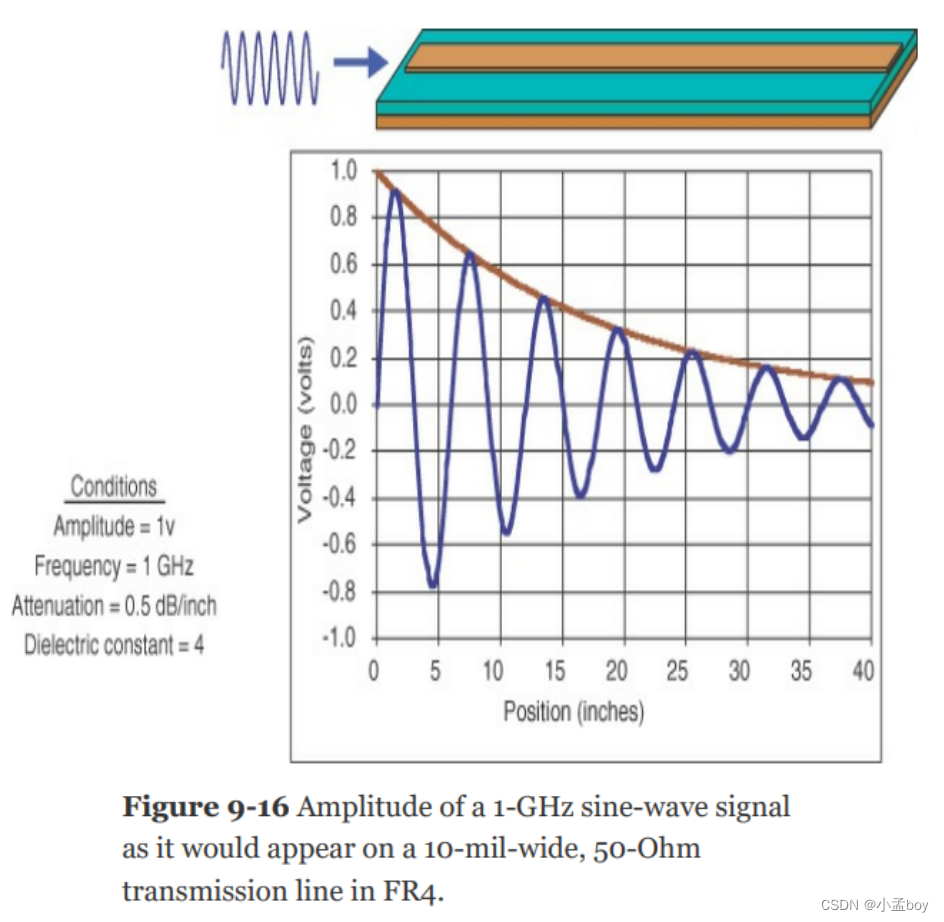
线路中的损耗对信号的主要影响是当信号沿线路长度传播时幅度减小。如果将幅度为 V 的正弦波电压信号引入传输线,则其幅度将随着传输线向下移动而下降。图 9-16 显示了如果我们可以冻结时间并观察直线上存在的正弦波,则正弦波在不同位置可能会是什么样子。这是针对 40 英寸长、50 欧姆 FR4 微带(迹线宽度为 10 毫英寸)上 1 GHz 正弦波的情况。
振幅随距离的变化不是线性的而是指数式的下降。这可以用以 e 为底或以 10 为底的指数来描述。使用以 e 为底的输出信号由下式给出:
![]()
其中:
Vd表示位置d的电压
d表示传输线某一位置
Vin表示输入电压波形的幅度
An表示总衰减
αn表示单位长度衰减
当使用以 e 为底的指数时,衰减单位是无量纲的,但仍被标记为 nepers,以纪念苏格兰人约翰·纳皮尔 (John Napier),他于 1614 年发表了以 e 为底的指数。Napiers 的一个令人困惑的方面是拼写。 Napiers、napers 和 nepers 都指同一个单位,并且是他名字的常用替代拼写。
虽然无量纲,但我们使用标签来提醒我们这是使用 e 基数的衰减。
例如,如果衰减为 1 napier,则最终幅度将为输入幅度的 exp(−1) = 37%。如果衰减为 2 纳皮尔,则输出幅度将为输入电压的 exp(−2) = 13%。同样,给定输入和输出幅度,可以从以下公式找到衰减:

该标志存在一些含糊之处。在所有无源互连中,永远不会有任何增益。输出电压始终小于输入电压。指数 0 将具有与输入幅度完全相同的输出幅度。减小幅度的唯一方法是使用负指数。减号应该明确地放在指数中,还是应该作为衰减的一部分?两种方法均按常规进行。衰减有时称为 -2 napiers 或 2 napiers。由于它总是被称为衰减,因此没有歧义。
通常,衰减被认为是大于零的正数。在这种观点中,负号不是衰减项的一部分,而是指数的一部分。
使用基数 10 比基数 e 更常见地描述衰减。输出幅度的形式为:

V(d) = 位置 d 线上的电压
d = 沿线的位置,以英寸为单位
Vin表示输入电压的幅度
AdB表示总衰减
αdB表示单位长度衰减,dB/inch
20表示将 dB 转换为幅度的系数,如下所述
用于描述衰减的单位是分贝或 dB。这些单位在整个工程中使用,无论它们出现在哪里,都会留下混乱。了解这个单位的起源将有助于消除混乱。
分贝是 100 多年前由亚历山大·格雷厄姆·贝尔 (Alexander Graham Bell) 创建的。他的职业生涯始于一名医生,研究和治疗有听力问题的儿童。为了量化听力损失的程度,他制定了一套标准化的声音强度,并量化了个人听到声音的能力。他发现响度的感觉并不取决于声音的功率强度,而是取决于功率强度的对数。他制定了一个响度等级,从能听到的最安静的耳语开始,以 0 为单位,而产生疼痛的声音则以 10 为单位。
所有其他声音均按实际测量功率水平的对数比率分布在此范围内。例如,如果响度从 1 增加到 2,则感觉响度增加了一倍。然而,测量到声音的实际功率电平增加了 102 /101 = 10。贝尔确定的是,感知响度变化的质量并不取决于功率电平变化,而是取决于与功率电平变化的对数成比例的单位。
贝尔响度的单位称为贝尔,其中 0 贝尔是可以听到的最安静的耳语。此后,每个声级的实际耳朵功率密度都被量化。在大约 2 kHz 的峰值灵敏度下可以感知到的最安静的声级是音阶的起点,0 Bell。它对应的功率密度为 10 -12 瓦/平方米。对于恰好位于疼痛阈值(10 响铃)的最大声音,功率级别为 10 -2 瓦/米。
随着感知响度的贝尔音阶得到广泛接受,最后一个 L 被去掉,变成了感知响度的贝尔音阶。随着时间的推移,人们发现,考虑到感知响度的范围令人难以置信,0 贝尔到 10 贝尔的音阶范围太小了。响度测量单位不再是贝尔,而是改为分贝,其中前言“deci”的意思是 1/10。现在,感知响度等级从耳语低端的 0 分贝(b 已小写)开始,在疼痛开始时为 100 分贝。分贝通常缩写为dB。
Tip:多年来,除了响度之外,分贝标度还被用于其他应用,但在每种情况下,分贝都保留其定义为两个幂比的对数。分贝标度最重要的属性是它始终指的是两个幂比的对数。
在几乎所有工程应用中,两个幂之比 P1 和 P0 的对数也以 Bels 为单位进行测量:Bels 数 = log(P1 /P0 )。由于 1 Bel = 10 分贝,因此比率(以 dB 为单位)为:

例如,如果功率增加 1000 倍,则增量(以 Bels 为单位)为 log(1000) = 3 Bels。以 dB 为单位,即 10 × 3 Bels = 30 dB。当输出功率仅为输入功率的 1% 时,功率电平的降低为
log(10 -2 ) = −2 Bels,或 10 × −2 Bels = −20 dB。
当功率电平因任意因素而变化时,变化可以用 dB 来描述,但计算对数值需要计算器。如果功率加倍,则 dB 变化为 10 × log(2) = 10 × 0.3 = 3 dB。我们经常使用“3 dB 变化”这一表述来指代功率电平加倍。如果功率变化下降 50%,则 dB 变化将为 10 × log(0.5) = −3 dB。
实际功率电平的比率可以通过以下方式从 dB 比率中提取:

第一步是将 dB 转换为 Bels。这是以 10 为底的指数。例如,如果以 dB 为单位的比率为 60,则功率电平比率为![]() 。如果dB值为−3 dB,则功率电平比为
。如果dB值为−3 dB,则功率电平比为
![]()
![]() 或50%。
或50%。
始终牢记有关 dB 标度的三个规则非常重要:
- dB 标度始终指两个功率或能量之比的对数。
- 当以 dB 为单位时,两个幂之比以 10 为底的指数就是 dB/10。
- 从 dB 转换为实际功率比时,使用系数 10。
每当测量其他两个量的比率时,功率的区别就很重要。当测量两个电压的比率 r(例如 V0 和 V1)时,单位是无量纲的:r = log(V1 /V0 )。但我们不能用 dB 来衡量比率,因为 dB 单位是指两个功率或能量的比率。电压不是能量;它是一个幅度。
我们可以参考与两个电压电平相关的功率之比,即rdB = 10 × log(P1 /P0 )。功率水平与电压水平有何关系?电压波中的能量与电压幅度的平方或 P ~ V 2成正比。
电压比(以 dB 为单位)实际上是相关功率的比,如下所示:
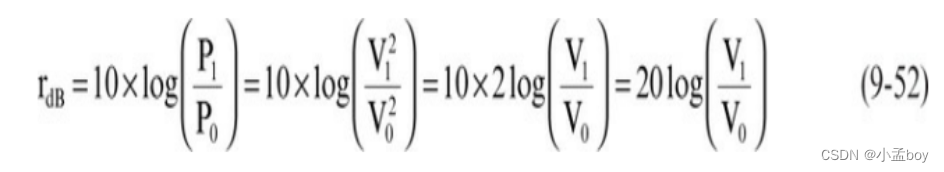
每当两个幅度的比率以 dB 为单位测量时,它是通过取其相关功率之比的对数来计算的。这相当于将电压比的对数乘以 20。
例如,电压从 1 v 到 10 v 的变化(以 dB 为单位)为 20 × log(10/1) = 20 dB。电压仅增加了 10 倍。然而,与 1 v 和 10 v 相对应的基础功率增加了 100 倍。这反映在功率电平 20 dB 的变化上。
dB 始终是功率变化的度量。当幅度减小到原始值的一半或减小 50% 时,最终值与初始值的比率(以 dB 为单位)为 20 × log(0.5) = 20 × -0.3 = -6 dB。如果电压降低 50%,则信号中的功率必定降低 (50%) 的平方或 25%。如果两个功率之比为 25%(以 dB 为单位),则为 10 × log(0.25) = 10 × −0.6 = −6 dB。
Tip:当提及能量或功率时,使用因子 10 来计算 dB 值。当提及幅度时,使用因子 20。幅度是诸如电压、电流或阻抗之类的量。
根据以 dB 为单位的比率,电压的实际比率可以计算为:

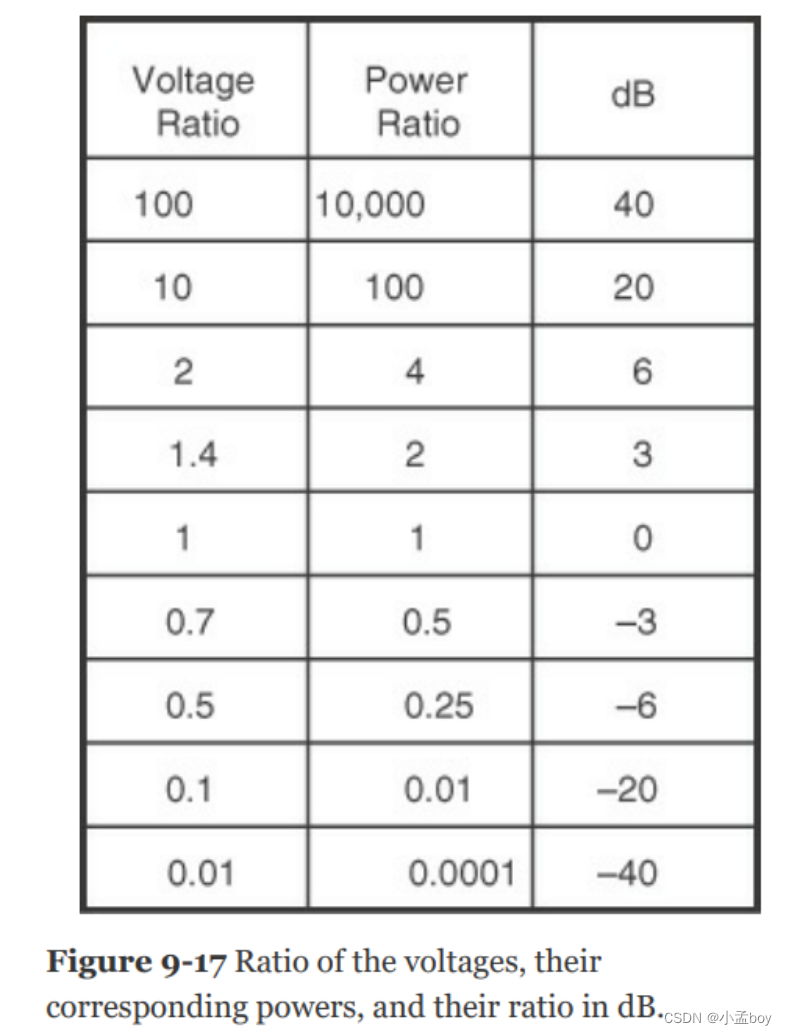
例如,如果以dB为单位的比率为20dB,则振幅的比率为10的(20/20)次方 = 10的一次方 = 10。如果以dB为单位的比率为-40dB,则电压的比率为10的(-40/20)次方 = 10的-2次方 = 0.01。如果以 dB 为单位的比率为负,则意味着最终值始终小于初始值。图 9-17 列出了电压比、相关功率以及以 dB 为单位的比值的几个示例。