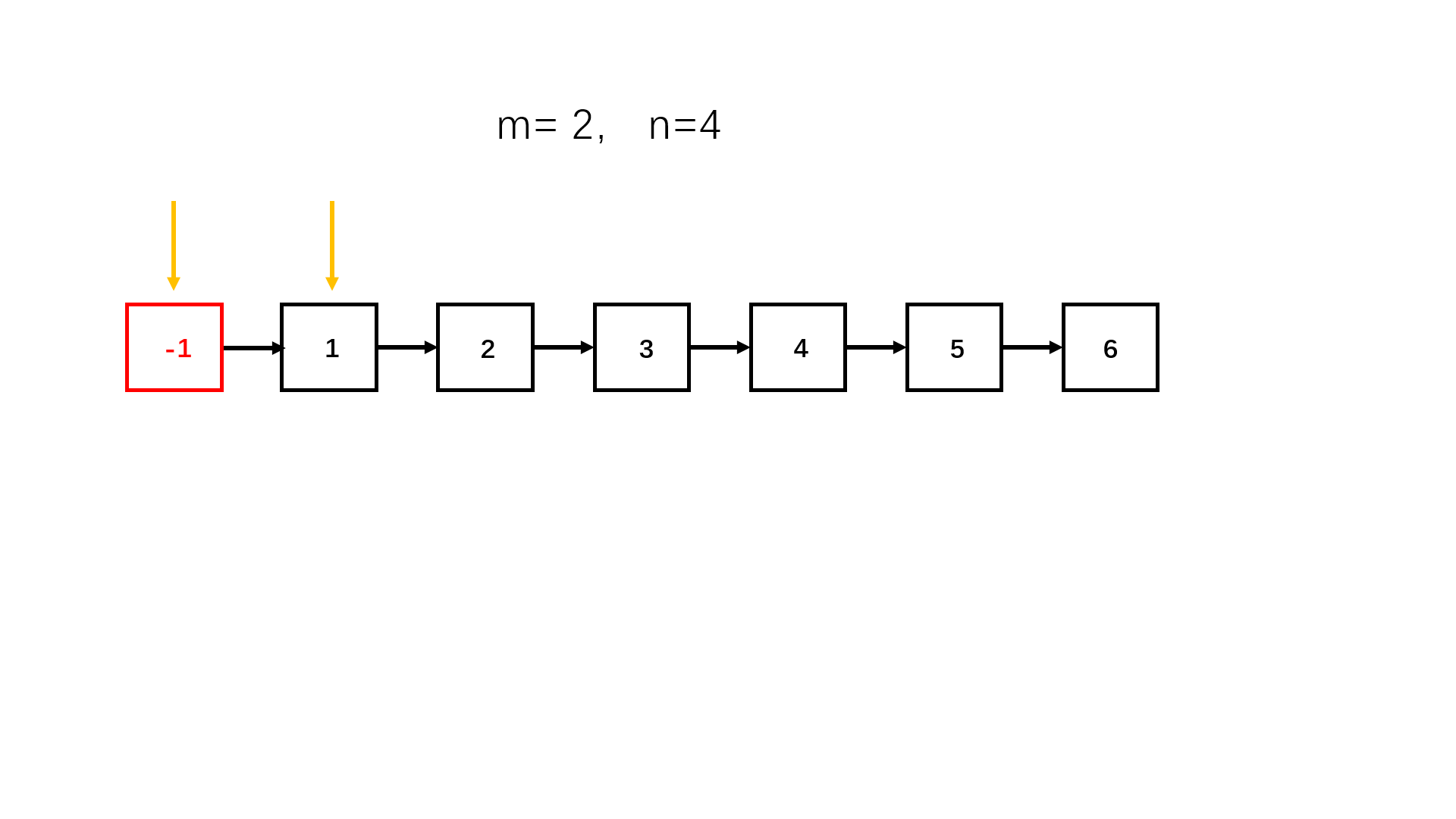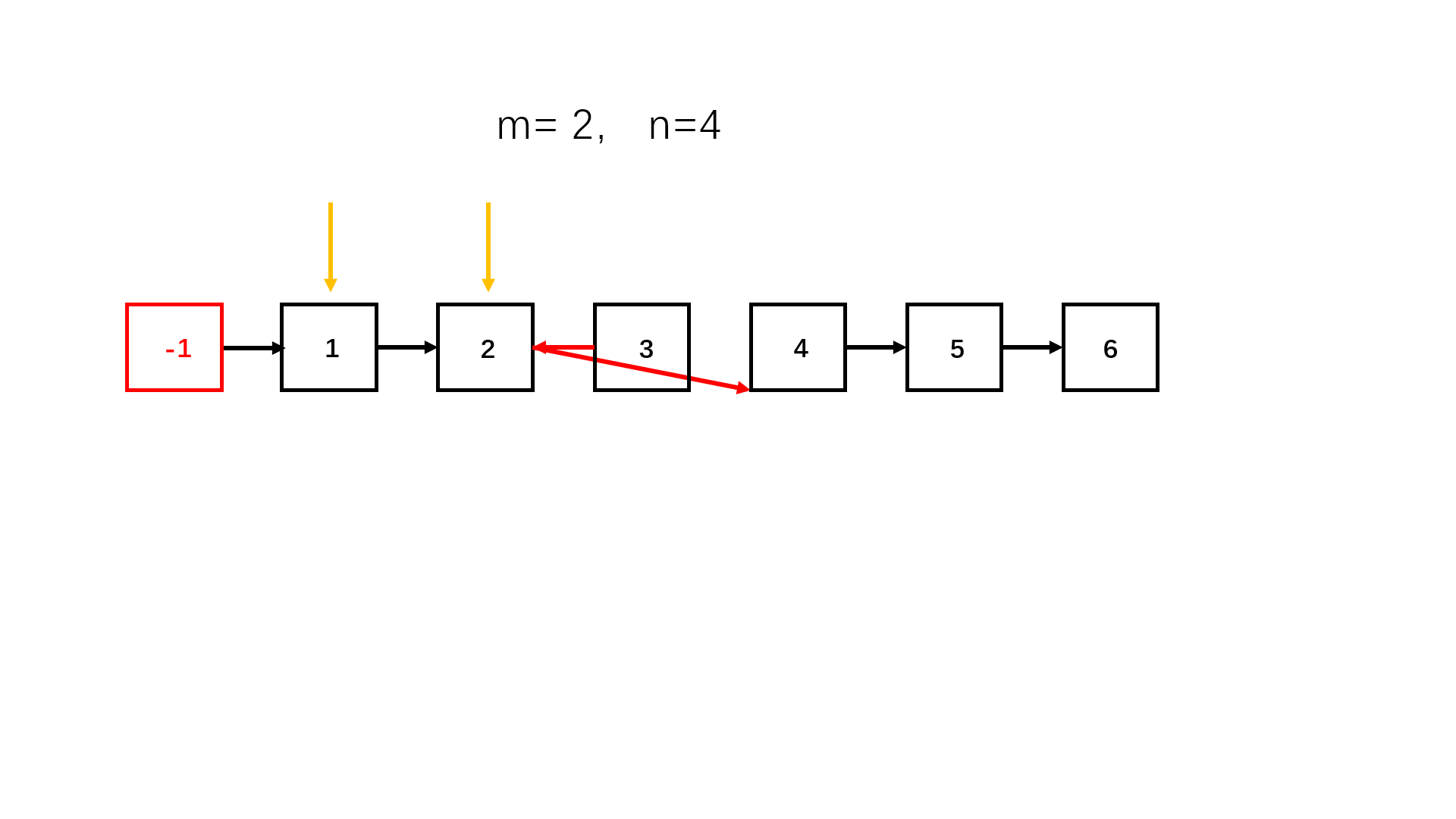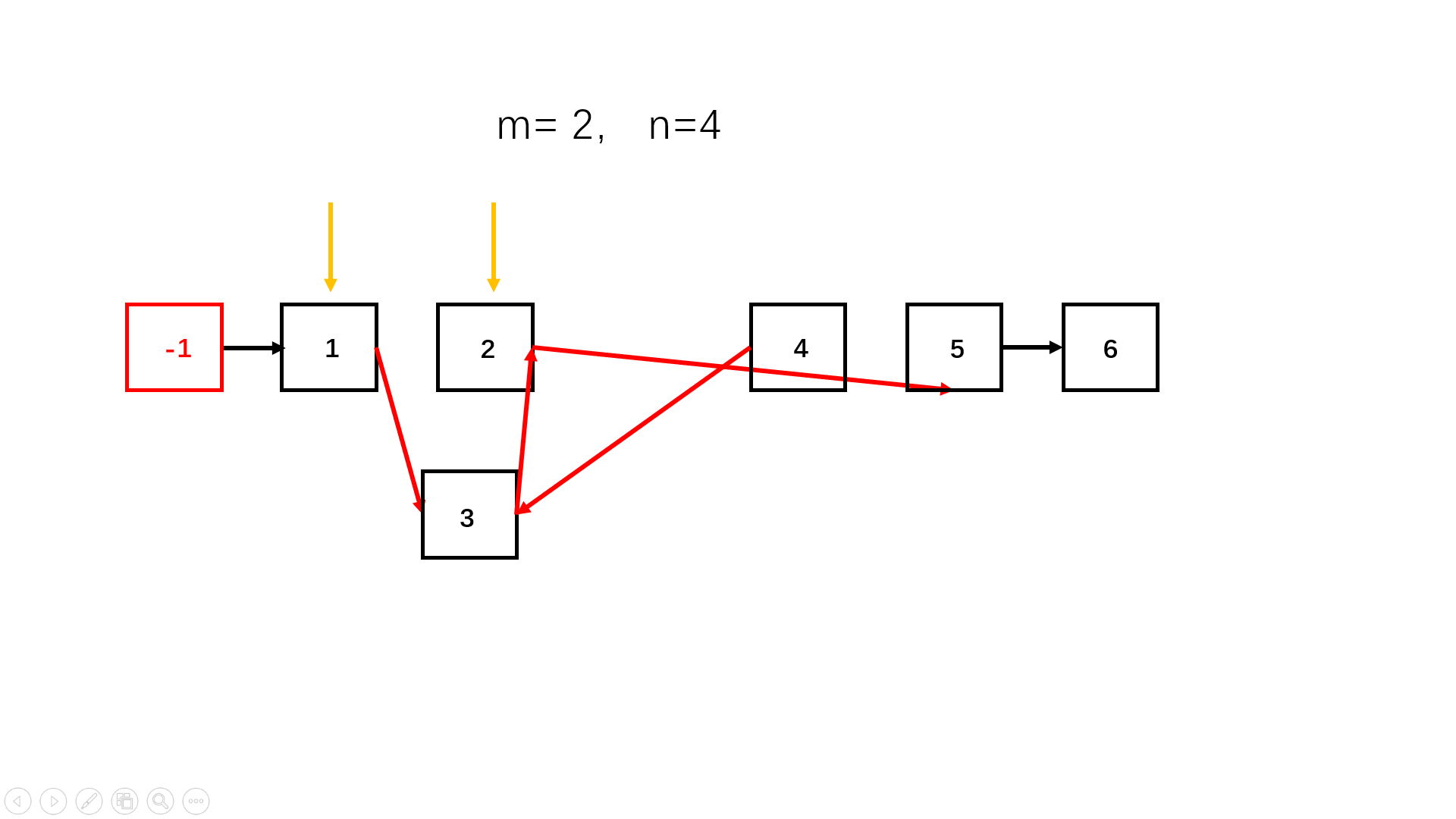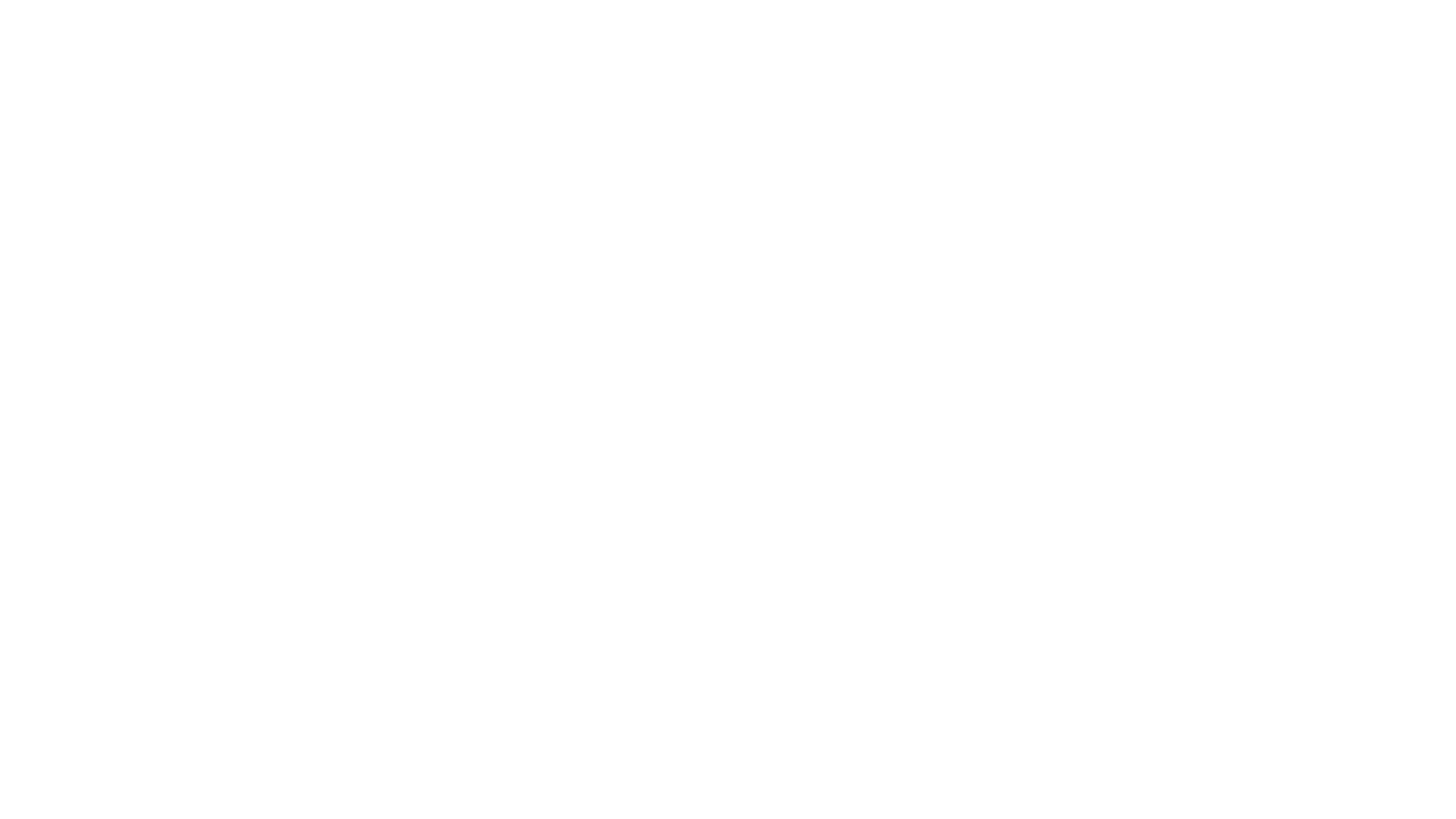【牛客面试必刷TOP101】Day15.BM2 链表内指定区间反转和BM3 链表中的节点每k个一组翻转

news2024/11/26 13:57:47

作者简介：大家好，我是未央；

博客首页：未央.303

系列专栏：牛客面试必刷TOP101

每日一句：人的一生，可以有所作为的时机只有一次，那就是现在！！！！！

文章目录

前言

一、链表内指定区间反转

题目描述

题目解析

二、链表中的节点每k个一组翻转

题目描述

题目解析

总结

前言

基于链表反转为基础的升级后的算法题目！！！

一、链表内指定区间反转

题目描述

描述：
将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转，要求时间复杂度 O(n)，空间复杂度 O(1)。

举例说明：
给出的链表为 1→2→3→4→5→NULL,

m=2,n=4,
返回1→4→3→2→5→NULL。

数据范围：链表长度 0<size≤1000，0<m≤n≤size，链表中每个节点的值满足∣val∣≤1000

要求：时间复杂度 O(n) ，空间复杂度 O(n)

进阶：时间复杂度 O(n)，空间复杂度 O(1)

示例1：

示例2：

题目解析

解题思路:

在学会了BM1.反转链表之后，要解决这个问题就很简单了，前一题是整个链表反转，这一题是部分反转，这上一题就是这道题的前置问题啊。那我们肯定是要先找到了第m个位置才能开始反转链表，而反转的部分就是从第m个位置到第n个位置，反转这部分的时候就参照BM1.反转链表;
while(cur != null){
    //断开链表，要记录后续一个
    ListNode temp = cur.next; 
    //当前的next指向前一个
    cur.next = pre; 
    //前一个更新为当前
    pre = cur; 
    //当前更新为刚刚记录的后一个
    cur = temp; 
}
解题步骤：

step 1：我们可以在链表前加一个表头，后续返回时去掉就好了，因为如果要从链表头的位置开始反转，在多了一个表头的情况下就能保证第一个节点永远不会反转，不会到后面去。
step 2：使用两个指针，一个指向当前节点，一个指向前序节点。
step 3：依次遍历链表，到第m个的位置。
step 4：对于从m到n这些个位置的节点，依次断掉指向后续的指针，反转指针方向。
step 5：返回时去掉我们添加的表头。

图示过程分析：

代码编写：

二、链表中的节点每k个一组翻转

题目描述

描述：

将给出的链表中的节点每 k 个一组翻转，返回翻转后的链表；

如果链表中的节点数不是 k 的倍数，将最后剩下的节点保持原样；

注意：你不能更改节点中的值，只能更改节点本身。

数据范围： 0≤n≤2000 ， 1≤k≤2000 ，链表中每个元素都满足 0≤val≤1000;
要求空间复杂度 O(1)，时间复杂度 O(n)

举例说明：

给定的链表是 1→2→3→4→5；

对于 k=2 , 你应该返回 2→1→4→3→5；

对于 k=3 , 你应该返回 3→2→1→4→5；

示例1：

示例2：

题目解析

解题思路：

方法：递归（推荐使用）

现在我们想一想，如果拿到一个链表，想要像上述一样分组翻转应该做些什么？首先肯定是分段吧，至少我们要先分成一组一组，才能够在组内翻转，之后就是组内翻转，最后是将反转后的分组连接。

但是连接的时候遇到问题了：首先如果能够翻转，链表第一个元素一定是第一组，它翻转之后就跑到后面去了，而第一组的末尾元素才是新的链表首，我们要返回的也是这个元素，而原本的链表首要连接下一组翻转后的头部，即翻转前的尾部，如果不建立新的链表，看起来就会非常难。但是如果我们从最后的一个组开始翻转，得到了最后一个组的链表首，是不是可以直接连在倒数第二个组翻转后的尾（即翻转前的头）后面，这样从后往前是不是看起来就容易多了。

怎样从后往前呢？我们这时候可以用到自上而下再自下而上的递归或者说栈。接下来我们说说为什么能用递归？如果这个链表有n个分组可以反转，我们首先对第一个分组反转，那么是不是接下来将剩余n−1个分组反转后的结果接在第一组后面就行了，那这剩余的n−1组就是一个子问题。我们来看看递归的三段式模版：

终止条件： 当进行到最后一个分组，即不足k次遍历到链表尾（0次也算），就将剩余的部分直接返回。
返回值： 每一级要返回的就是翻转后的这一分组的头，以及连接好它后面所有翻转好的分组链表。
本级任务： 对于每个子问题，先遍历k次，找到该组结尾在哪里，然后从这一组开头遍历到结尾，依次翻转，结尾就可以作为下一个分组的开头，而先前指向开头的元素已经跑到了这一分组的最后，可以用它来连接它后面的子问题，即后面分组的头。

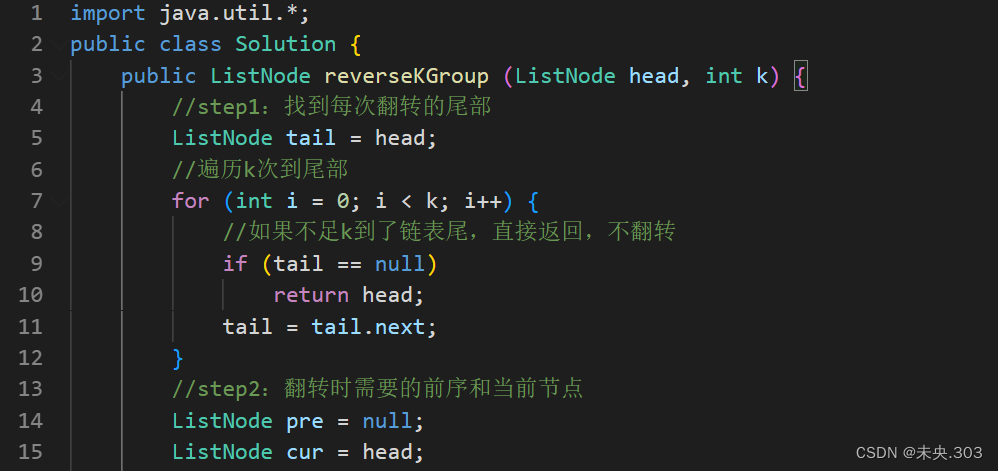
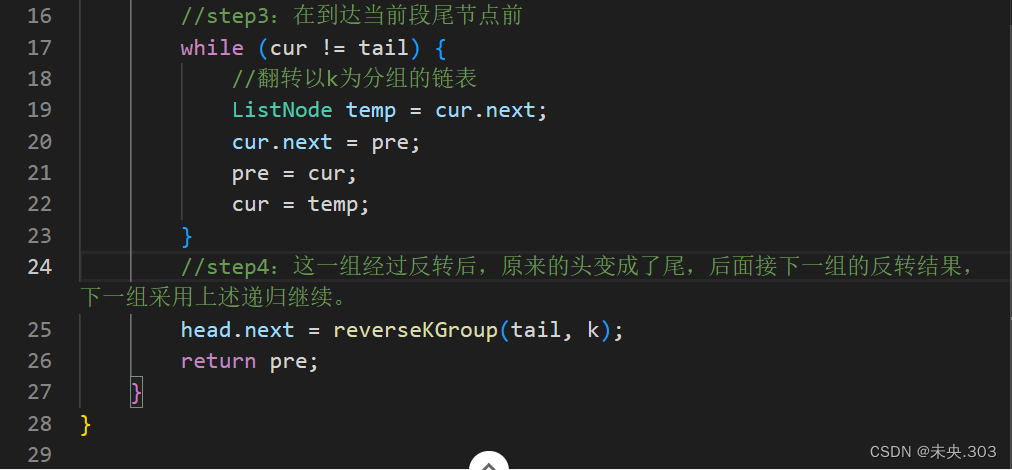
解题步骤：

step 1：每次从进入函数的头节点优先遍历链表k次，分出一组，若是后续不足k个节点，不用反转直接返回头。
step 2：从进入函数的头节点开始，依次反转接下来的一组链表，反转过程同BM1.反转链表。
step 3：这一组经过反转后，原来的头变成了尾，后面接下一组的反转结果，下一组采用上述递归继续。

图示过程解析：