本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

示例 1：

输入：nums = [2,2,3,2]
输出：3

示例 2：

输入：nums = [0,1,0,1,0,1,99]
输出：99

提示：

• 1 <= nums.length <= 3 * 10^4
• -2^31 <= nums[i] <= 2^31 - 1
• nums 中，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次

---

可使用哈希映射统计数组中每个元素的出现次数。对于哈希映射中的每个键值对，键表示一个元素，值表示其出现的次数。在统计完成后，我们遍历哈希映射即可找出只出现一次的元素。这里不对代码进行说明。

解法1 依次确定每一个二进制位

为了方便叙述，我们称「只出现了一次的元素」为「答案」。

由于数组中的元素都在 $int$（即 $32$ 位整数）范围内，因此可以依次计算答案的每一个二进制位是 $0$ 还是 $1$ 。

具体地，考虑答案的第 $i$ 个二进制位（$i$ 从 $0$ 开始编号），它可能为 $0$ 或 $1$。对于数组中非答案的元素，每一个元素都出现了 $3$ 次，对应着第 $i$ 个二进制位的 $3$ 个 $0$ 或 $3$ 个 $1$，无论是哪一种情况，它们的和都是 $3$ 的倍数（即和为 $0$ 或 $3$）。因此：

答案的第 $i$ 个二进制位，就是数组中所有元素的第 $i$ 个二进制位之和除以 $3$ 的余数。

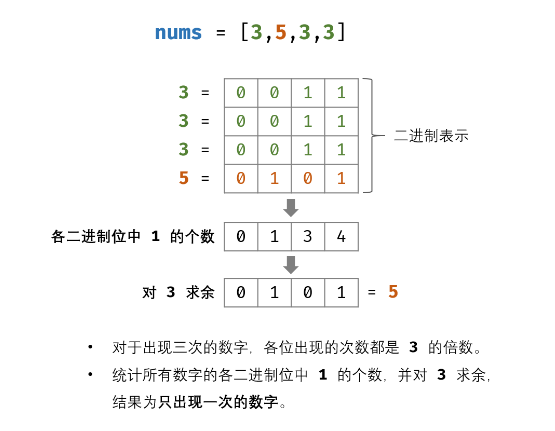
这样一来，对于数组中的每一个元素 $x$ ，我们使用位运算 $\text{(x >> i) \& 1}$ 得到 $x$ 的第 $i$ 个二进制位，并将它们相加再对 $3$ 取余，得到的结果一定为 $0$ 或 $1$，即为答案的第 $i$ 个二进制位。

细节：需要注意的是，如果使用的语言对「有符号整数类型」和「无符号整数类型」没有区分，那么可能会得到错误的答案。这是因为「有符号整数类型」（即 $\text{int}$ 类型）的第 $31$ 个二进制位（即最高位）是补码意义下的符号位，对应着 $-2^{31}$ ，而「无符号整数类型」由于没有符号，第 $31$ 个二进制位对应着 $2^{31}$ 。因此在某些语言（例如 Python）中需要对最高位进行特殊判断。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans = 0;
        for (int i = 0; i < 32; ++i) {
            int total = 0;
            for (int num : nums) 
                total += ((num >> i) & 1); // 所有数的第i个二进制位之和
            if (total % 3) ans |= (1 << i); // 设置答案的第i个二进制位
        }
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$O(n\log C)$ ，其中 $n$ 是数组的长度，$C$ 是元素的数据范围，在本题中 $\log C=\log 2^{32}=32$ ，也就是我们需要遍历第 $0\sim 31$ 个二进制位。
• 空间复杂度：$O(1)$ 。

实际上本方法还可继续优化。我们设置三个数 $one,two,three$ 分别表示所有元素的所有二进制位中出现一次、二次、三次的位。最后的 $one$ 就是答案。过程如下，设 $num$ 为当前元素：

• 使用 $one\&num$ 表示「$num$ 与 $one$ 中同时出现的二进制位」表示的值，这些二进制位目前出现了两次，因此 $two|=(one\&num)$
• 使用 $onexornum$ ，这表示设置那些出现了一次的二进制位，出现了两次的二进制位会被置零。
• 再令 $one\&two$ 表示「$one$ 与 $two$ 中同时出现的二进制位」表示的值，这些二进制位目前出现了三次，令 $three=(one\&two)$ 。
• 相应的位出现了三次，则（和对 $3$ 取余一样）将该位重置为 $0$ ——令 $two\&=three,one\&=three$ 。

最后返回 $one$ 作为答案，它记录了那些只出现一次的二进制位，在本题中就等于「答案」的值。

class Solution {
public: 
    int singleNumber(vector<int>& nums) {
        int one = 0, two = 0, three;
        for (int num : nums) {
            // two的相应的位等于1，表示该位出现2次
            two |= (one & num);
            // one的相应的位等于1，表示该位出现1次
            one ^= num;
            // three的相应的位等于1，表示该位出现3次
            three = (one & two);
            // 如果相应的位出现3次，则该位重置为0
            two &= ~three;
            one &= ~three;
        }
        return one;
    }
};

---

解法2 数字电路设计

方法2以及后续进行优化的方法3需要有一定的数字电路设计的基础。需要对以下知识有一定的了解：

• 简单的门电路（例如与门、异或门等）
• 给定数字电路输入和输出（真值表），使用门电路设计出一种满足要求的数字电路结构

门电路表示：我们将会用到四种门电路，使用的符号如下：

• 非门：我们用 $A^{\prime }$ 表示输入为 $A$ 的非门的输出；
• 与门：我们用 $AB$ 表示输入为 $A$ 和 $B$ 的与门的输出。由于「与运算」具有结合律，因此如果同时用了多个与门（例如将 $A$ 和 $B$ 进行与运算后，再和 $C$ 进行与运算），我们可以将多个输入写在一起（例如 $ABC$ ）；
• 或门：我们用 $A+B$ 表示输入为 $A$ 和 $B$ 的或门的输出。同样地，多个或门可以写在一起（例如 $A+B+C$ ）；
• 异或门：我们用 $A\oplus B$ 表示输入为 $A$ 和 $B$ 的异或门的输出。同样的，多个异或门可以写在一起（例如 $A\oplus B\oplus C$ ）。

在方法二中，我们是依次处理每一个二进制位的，那么时间复杂度中就引入了 $O(\log C)$ 这一项。既然我们在对两个整数进行普通的二元运算时，都是将它们看成整体进行处理的，那么我们是否能以普通的二元运算为基础，同时处理所有的二进制位？

答案是可以的。我们可以使用一个「黑盒」存储当前遍历过的所有整数。「黑盒」的第 $i$ 位为 { 0 , 1 , 2 } \{ 0, 1, 2 \} {0,1,2} 三者之一，表示当前遍历过的所有整数的第 $i$ 位之和除以 $3$ 的余数。但由于二进制表示中只有 $0$ 和 $1$ 而没有 $2$ ，因此我们可以考虑在「黑盒」中使用两个整数来进行存储，即：

黑盒中存储了两个整数 $a$ 和 $b$ ，且会有三种情况：

• $a$ 的第 $i$ 位为 $0$ 且 $b$ 的第 $i$ 位为 $0$，表示 $0$ ；
• $a$ 的第 $i$ 位为 $0$ 且 $b$ 的第 $i$ 位为 $1$，表示 $1$ ；
• $a$ 的第 $i$ 位为 $1$ 且 $b$ 的第 $i$ 位为 $0$ ，表示 $2$ 。

为了方便叙述，我们用 $(00)$ 表示 $a$ 的第 $i$ 位为 $0$ 且 $b$ 的第 $i$ 位为 $0$，其余的情况类似。

当我们遍历到一个新的整数 $x$ 时，对于 $x$ 的第 $i$ 位 $x_i$ ，如果 $x_i=0$ ，那么 $a$ 和 $b$ 的第 $i$ 位不变；如果 $x_i=1$ ，那么 $a$ 和 $b$ 的第 $i$ 位按照 $(00)\to (01)\to (10)\to (00)$ 这一循环进行变化。因此我们可以得出下面的真值表：

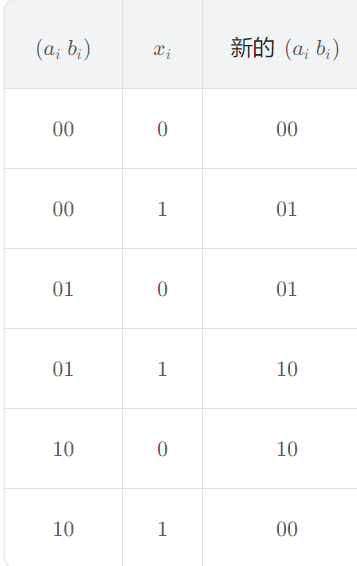
当我们考虑输出为 $a_i$ 时，根据真值表可以设计出电路：
$$a_i=a_i^{\prime }{b}_i{x}_i+a_i{b}_i^{\prime }{x}_i^{\prime }$$
当我们考虑输出为 $b_i$ 时，根据真值表可以设计出电路：
$$b_i=a_i^{\prime }{b}_i^{\prime }{x}_i+a_i^{\prime }{b}_i{x}_i^{\prime }=a_i^{\prime }(b_i\oplus x_i)$$
将上面的电路逻辑运算转换为等价的整数位运算，最终的转换规则即为：

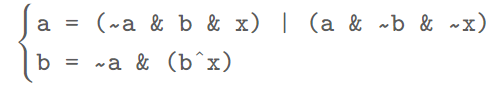
当我们遍历完数组中的所有元素后，$(a_i{b}_i)$ 要么是 $(00)$ ，表示答案的第 $i$ 位是 $0$；要么是 $(01)$ ，表示答案的第 $i$ 位是 $1$ 。因此我们只需要返回 $b$ 作为答案即可。

细节：由于电路中的 $a_i$​ 和 $b_i$ 是「同时」得出结果的（同时根据旧有的 $a,b$ 得到新的 $a,b$ ），因此我们在计算 $a$ 和 $b$ 时，需要使用临时变量暂存它们之前的值，再使用转换规则进行计算。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a = 0, b = 0;
        for (int num: nums) {
            tie(a, b) = pair{(~a & b & num) | (a & ~b & ~num), ~a & (b ^ num)};
        }
        return b;
    }
};

复杂度分析：

• 时间复杂度：$O(n)$ ，其中 $n$ 是数组的长度。
• 空间复杂度：$O(1)$ 。

---

解法3 数字电路设计优化

我们发现方法三中计算 $b$ 的规则较为简单，而 $a$ 的规则较为麻烦，因此可以将「同时计算」改为「分别计算」，即先计算出 $b$，再拿新的 $b$ 值计算 $a$（这也是转换的实际情况）。

对于原始的真值表：

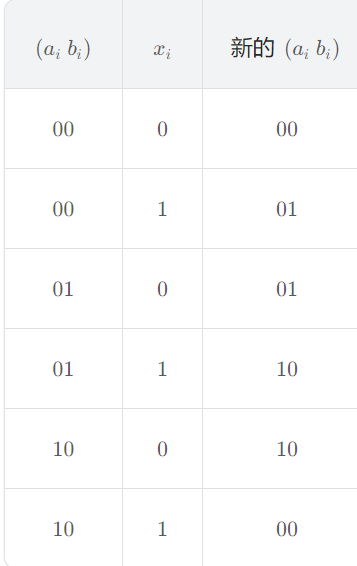
我们将第一列的 $b_i$​ 替换新的 $b_i$ 即可得到：

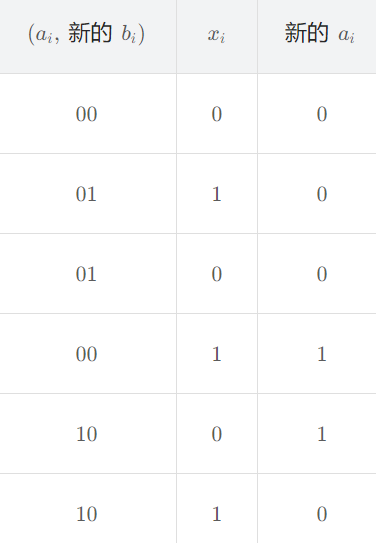
根据真值表可以设计出电路：
$$a_i=a_i^{\prime }{b}_i^{\prime }{x}_i+a_i{b}_i^{\prime }{x}_i^{\prime }=b_i^{\prime }(a_i\oplus x_i)$$
这样就与 $b_i$​ 的电路逻辑非常类似了。最终的转换规则即为：

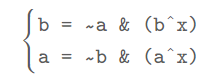
需要注意先计算 $b$，再计算 $a$。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a = 0, b = 0;
        for (int num: nums) {
            b = ~a & (b ^ num);
            a = ~b & (a ^ num);
        }
        return b;
    }
};

复杂度分析：

• 时间复杂度：$O(n)$ ，其中 $n$ 是数组的长度。
• 空间复杂度：$O(1)$ 。

---

解法4 DFA（余数状态转换）

如方法1所述，对于所有数字中的某二进制位 $1$ 的个数，存在 $3$ 种状态，即对 $3$ 余数为 $0,1,2$ 。

• 若输入二进制位 $1$ ，则状态按照以下顺序转换；
• 若输入二进制位 $0$ ，则状态不变
  $$0\to 1\to 2\to 0\to \cdots$$
  
  如下图所示，同样由于二进制只能表示 $0,1$ ，因此需要使用两个二进制位来表示 $3$ 个状态。设此两位分别为 $two,one$ ，则状态转换变为：
  $$00\to 01\to 10\to 00\to \cdots$$
  
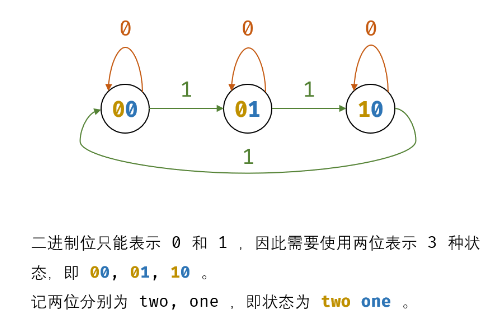
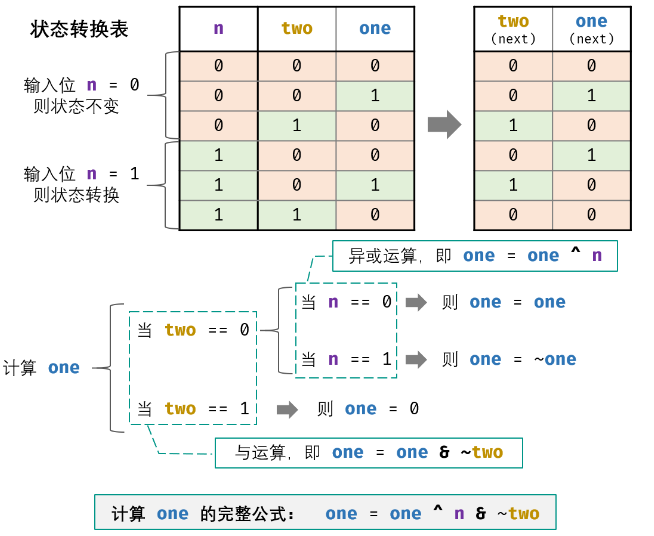
  接下来通过状态转换表导出状态转换的计算公式。
• 计算 $one$ 的方法：设当前状态为 $twoone$ ，此时输入二进制位 $n$ 。如下图所示：
• 计算 $two$ 的方法：由于是先计算 $one$ ，因此应在新 $one$ 的基础上计算 $two$ 。如下图所示，修改为新 $one$ 后，得到了新的状态图。观察发现，可用同样的方法计算 $two$ ：
  

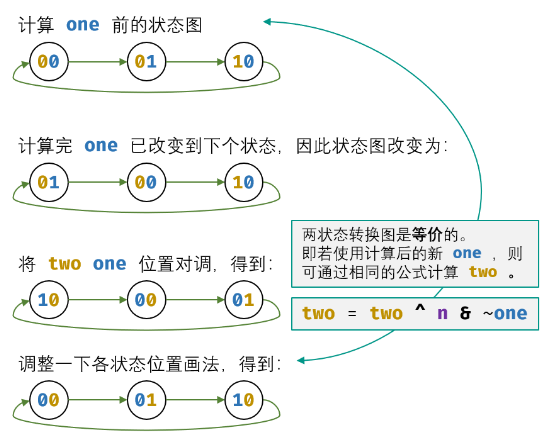
以上是对数字的二进制中 “一位” 的分析，而 $int$ 类型的其他 $31$ 位具有相同的运算规则，因此可将以上公式直接套用在 $32$ 位数上。

遍历完所有数字后，各二进制位都处于状态 $00$ 和状态 $01$ （取决于 “只出现一次的数字” 的各二进制位是 $1$ 还是 $0$ ），而此两状态是由 $one$ 来记录的（此两状态下 $twos$ 恒为 $0$ ），因此返回 $ones$ 即可。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a = 0, b = 0;
        for (int num: nums) {
            b = (b ^ num) & ~a;
            a = (a ^ num) & ~b;
        }
        return b;
    }
};