2652. 倍数求和
- 题目
- 方法-【枚举】 & 题目特征-【求计算在给定范围内满足某种条件的整数之和】
- 方法-【容斥原理】 & 题目特征-【计算满足多个条件的元素之和,并且需要避免重复计数】
题目
题目链接:https://leetcode.cn/problems/sum-multiples/description/
给你一个正整数 n ,请你计算在 [1,n] 范围内能被 3、5、7 整除的所有整数之和。
返回一个整数,用于表示给定范围内所有满足约束条件的数字之和。
方法-【枚举】 & 题目特征-【求计算在给定范围内满足某种条件的整数之和】
class Solution {
public:
int sumOfMultiples(int n) {
int sum = 0;
for (int i = 1; i <= n; i++)
if (i % 3 == 0 || i % 5 == 0 || i % 7 == 0)
sum += i;
return sum;
}
};
方法-【容斥原理】 & 题目特征-【计算满足多个条件的元素之和,并且需要避免重复计数】
举个例子,当我们想要计算一共有多少只动物,但有些动物同时属于几个类别,我们可以使用容斥原理。
假设我们有三个类别的动物:猫、狗和兔子,并且我们有以下信息:
- 喜欢猫的人数10
- 喜欢狗的人数15
- 喜欢兔子的人数8
我们想要找到同时喜欢三种动物的人数。
如果我们简单地将每个类别的动物数量相加,我们会得到10 + 15 + 8 = 33只动物。但这样计算会有重复计数的问题,因为有些动物同时属于多个类别。
为了避免重复计数,我们可以使用容斥原理。根据容斥原理,我们需要:
- 将每个类别的动物数量相加;
- 减去同时属于两个类别的动物数量;
- 加上同时属于三个类别的动物数量。
因此,我们可以计算:10 + 15 + 8 - (猫 & 狗的数量) - (狗 & 兔子的数量) - (猫 & 狗 & 兔子的数量) = 1只动物。
通过应用容斥原理,我们得到了正确的结果,即一共有1只动物,避免了重复计数的问题。
这个题目和答案是乱写的,主要看题目特征和方法的匹配 — 之所以使用 xx方法(容斥原理),是因为题目有 xx 特征。
在 2652 这题:
- 集合 A:能被 2 整除的数;
- 集合 B:能被 3 整除的数;
- 集合 C:能被 5 整除的数。
我们希望计算在给定范围内满足这些条件的数的总数,同时避免重复计数。
那我们需要容斥原理才能做到全面完整、不重不漏的计数。
具体看官网题解:

f(n, m) 表示在区间 [1, n] 内能被 m 整除的整数之和。
f(n, m) 函数计算方法:
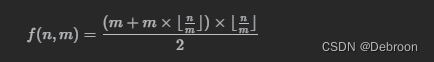
class Solution {
private:
int f(int n, int k){
int cnt = n / k; // cnt * k 为小于等于n的最大数字
return (k + cnt * k) * cnt / 2; // 等差数列求和公式
}
public:
int sumOfMultiples(int n) {
return f(n, 3) + f(n, 5) + f(n, 7) - f(n, 3*5) - f(n, 3 * 7) - f(n,5*7) + f(n, 3 * 5 * 7);
}
};
或者
class Solution {
public:
int sumOfMultiples(int n) {
int sum = 0;
int div3 = n / 3;
int div5 = n / 5;
int div7 = n / 7;
int div15 = n / 15;
int div21 = n / 21;
int div35 = n / 35;
int div105 = n / 105;
sum = 3 * div3 * (div3 + 1) / 2
+ 5 * div5 * (div5 + 1) / 2
+ 7 * div7 * (div7 + 1) / 2
- 15 * div15 * (div15 + 1) / 2
- 21 * div21 * (div21 + 1) / 2
- 35 * div35 * (div35 + 1) / 2
+ 105 * div105 * (div105 + 1) / 2;
return sum;
}
};