浅谈估值模型：估值幻觉

1：本文是方正证券研报《如何打破“估值幻觉”》【1】的复现研究；

2：本文主要为理念的讲解，模型也是笔者自建，主要数据通过Tushare金融大数据平台接口获取，部分数据通过Wind金融终端获取；

3：文中假设与观点是基于笔者对模型及数据的一孔之见，若有不同见解欢迎随时留言交流；

4：模型实现基于python3.8；

本文主要内容如下：

1. 什么是估值幻觉

2. 消除估值幻觉

3. 复现结果

4. 策略构建

4.1 回测结果

4.2 策略对比

5. 代码实现

5.1 A股非金融加权分位数

5.2 整体法PE

5.3 行业分位数法估值重构

6. 总结

7. 引用

8. 往期精选

1. 什么是估值幻觉

近年来，我国上市公司的行业结构占比发生较大变化，图一展示了2013年10月及2023年10月A股的各行业市值占比。在这10年中，金融行业占比由原来的22.00%跌至15.07%；能源行业占比由原来的10.92%跌至4.70%；而信息技术行业由原来的8.09%上升至17.25%；消费行业由5.64%上升至9.16%。方正证券认为，不同行业估值水平的差异及行业结构的变迁会导致市场估值的中枢发生变化，因此将现在与10年前的估值高低直接进行比较，结果就一定程度上失真了，这也是“估值幻觉”的由来。

图一：A股行业市值占比变化（数据来源：WInd）

2. 消除估值幻觉

市场上主流的估值方式是通过市值加权计算指数每天PE、PB等指标的时间序列，然后通过时间序列数据计算出历史所处的分位。方正证券提出一种新的分位数法用以消除行业结构造成的估值幻觉，该分位数法是先分位，再加权。主要有两个步骤：1）计算个股的历史分位数，2）将个股分位数进行市值加权计算全市场的分位数。

通过这样的方式先将原始数据统一到0-100%的区间内，消除行业间估值分位数差异大的偏差，实现了个股估值数据的标准化。因此，即使发行了很多估值中枢本身比较高的公司股票，也不会导致市场估值产生不合理的抬升。此外，方正证券还对估值较低，权重占比较大的金融板块进行了剔除，最后得到A股非金融的加权分位数估值水平，如图二所示。就PE估值水平来看，已经降至2012年及2019年相似的历史低位，且当前PE分位数在40%左右，A股2010年至今的平均分位数在54%左右：

图二：A股非金融的加权分位数

不得不说这是个很棒的思路和数据处理方式，但是笔者在进行研究复现后得到的结果却产生了一定的差别。

3. 复现结果

笔者选取了沪深主板，创业板及科创板作为样本构建指数，包含已退市和停牌股票共计5065家公司2005年至今的所有数据。按申万一级行业分类口径剔除银行及非银金融板块，删除每家公司上市前20个交易日波动较大的数据，通过分位数法对指数估值分位进行重构后得到PE TTM估值分位数走势如下：

图三：A股非金融加权分位数(PE TTM,剔除金融板块)

首先，图三中的2013年，19年和23年的估值低位并不是图二那样在同一水平线上，而是呈现逐步抬升的趋势。其次，图二中12年-13年的走势与图三出现较大差异，图二中低点出现在13年，而图二中出现在12年初。最后，图三的估值中枢也低于图二的54%。笔者又利用整体法计算了一次A股的剔除金融板块与不剔除金融板块下的PE，得到图四和图五：

图四：整体法下的PE TTM

图五：整体法下的PE TTM（剔除金融板块）

从图四和图五来看，虽然剔除掉金融板块使得A股PE水平抬升了，但对于低点还是呈现出逐步抬升的趋势。换句话说，低点的整体抬升并不是由于金融板块造成的。那么接下来就考虑是不是数据本身的问题，由于是选取了所有的历史数据，而PE指标对于亏损企业来说并没有什么意义。下面笔者又将历史上处于亏损状态的企业数据剔除，再次计算分位数得到图六：

图六：A股非金融加权分位数（PE TTM，剔除负值）

有意思的来了，22年的低点降至与18年低点差不多的位置，但是13年的低点依旧远低于18年和22年的低点，这还是很难解释。笔者又计算了PB指标的情况，如图七。PB的走势和PE非常相近，在剔除金融板块后依然呈现低点逐步抬升的现象，这和图二研报中的PB走势可以说是大相径庭了：

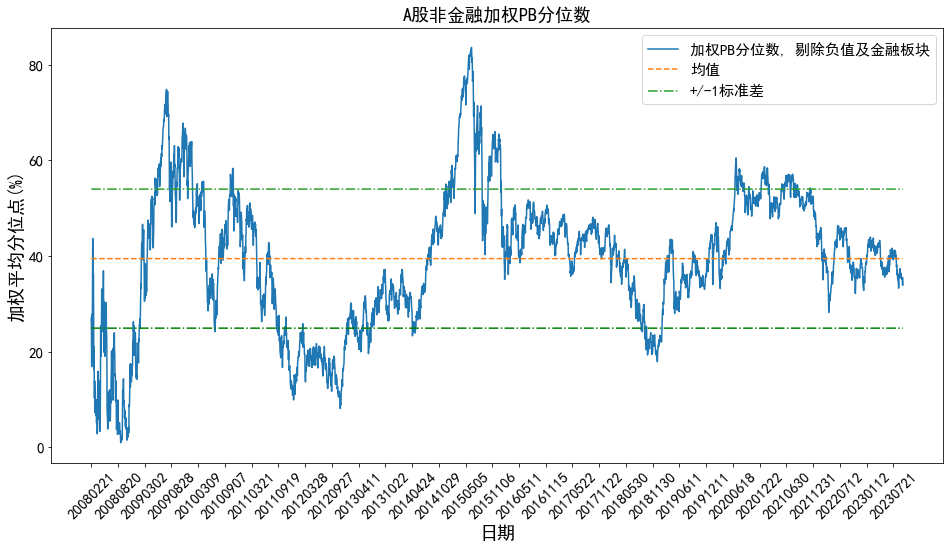
图七：A股非金融加权PB分位数

除了指数，该研报还对行业进行了估值重构，笔者对通信行业进行计算后得到图八，该行业的确与研报中的结果一致，通信行业目前分位数已经处于历史高位：

图八：通信行业分位数法加权分位数结果（PE TTM)

当然，除了通信行业，还可以对其它30个申万一级行业进行重构，并且与原始的估值数据作比较。以农林牧渔板块为例，将申万原始估值分位与分位数法修正的分位数画在同一张图上得到图九：

图九：农林牧渔板块估值分位数对比（PE TTM，时间序列数据）

当然，除了时间序列，还可以对截面数据进行对比。将所有行业估值进行重构，并且将2023年10月13日的原始分位点和修正分位点画在散点图上，得到图十：

图十：申万一级行业板块估值分位数对比（PE TTM，截面数据）

通过这样做可以更加直观的看到全行业的估值分布情况。如图十所示，数据点靠近图十左上角说明看似低估，但实际被高估，例如通信行业；数据点靠近图十右下角则说明看似高估，但实际被低估，例如电子和基础化工。数据点落在红色虚线附近时，说明原始分位点和修正的分位点相近，例如电力设备、计算机和商贸零售等。

4. 策略构建

尽管前面对各行业进行了估值重构，但笔者还想知道重构后的估值分位有效性如何。当然最直接的方式就是依据这个数据进行交易，但由于没有任何实盘记录，只能借助数据进行模拟回测。笔者选取申万一级行业指数2013年至今的涨跌幅数据和估值数据，在每个月月底最后一个交易日对申万31个行业进行PE TTM估值排序，收盘价买入最低估的两个行业指数，持有到下个月月底最后一个交易日时再进行一次行业重估，如果发现有PE TTM估值更低的行业，则开盘时卖出之前持有的高估行业，再以收盘价买入最新的两个估值最低行业。

需要说明的是，这个策略只是为了验证分位数法重估行业的指标是不是可以带来较为不错的择时效果，但实际上申万行业指数并没有多少对应的ETF可供实盘买卖。

4.1 回测结果

经过回测，策略的净值表现如图十一：

图十一：分位数法策略及沪深300净值走势

策略相关的业绩指标如下：

指标	策略	基准（沪深300）
年化收益率(%)	-3.96	3.10
夏普	-0.14	0.12
IR	-3.22	\
最大回撤(%)	66.45	46.70

表一：分位数法策略业绩指标

从图十一和表一来看，该策略近十年来大幅跑输沪深300指数，策略总回报-34.77%，回撤方面也远高于指数，总的来看该策略并不是一个好策略。

4.2 策略对比

笔者还对原始估值数据进行策略构建，方法和之前完全一样，只是将重构的估值数据替换成原始的PE TTM数据再次进行回测，得到净值走势如图十二：

图十二：原始估值策略及沪深300净值走势

策略相关的业绩指标如下：

指标	策略	基准（沪深300）
年化收益率(%)	8.14	3.10
夏普	0.29	0.12
IR	2.40	\
最大回撤(%)	46.13	46.70

表二：原始估值策略业绩指标

从图十二和表二来看，使用原始的估值数据反而可以一定程度上跑赢沪深300指数，该策略总回报和年化收益分别为128.89%和8.14%，高于分位数法策略的-34.77%和-3.96%，信息比率达到2.4。该策略回撤46.13%，与指数非常相近，但表现远好于分位数法策略的66.45%，总的来看该策略虽然年化回报偏低，回撤也大，但却是好过分位数法策略太多。

其实这个策略只是个很粗糙的策略，例如并不是所有行业都适合PE指标估值；其次，该策略进行的是基于时间的月频定期调仓，并不能算是很灵活；最后，申万一级行业指数只是个分类标准，实际上并没有多少跟踪申万行业一级行业指数的ETF，实盘意义较低。感兴趣的读者可以自行改进设计，也欢迎留言交流。

5. 代码实现

由于策略实现需要用到几千家公司十几年的数据，笔者借助代码实现。下面的代码只包含文章第3部分的图表。数据方面笔者选择了Tushare金融大数据平台，需要申请账号才能调用相关借口。

首先导入需要的模块：

import pandas as pd
import numpy as np
import tushare as ts
import time 
import matplotlib.pyplot as plt
from adjustText import adjust_text


# 初始化pro接口
token = ## 输入自己的密钥
ts.set_token(token)
pro = ts.pro_api()

文中涉及到的很多图表都有中文，需要对matplotlib进行简单设置，不然会弹出警告且无法显示：

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

5.1 A股非金融加权分位数

首先是图三，需要注意的是Tushare现成的估值指标数据都是剔除负值的，如果要计算包含负值数据，只能拿财务数据和市值数据一家家公司算。先分别获取所有公司列表，包含主板、科创板和创业板。然后把它们全都合并到一张大表里：

data = pro.stock_basic(exchange='', market = "主板", list_status='', fields='ts_code,symbol,name,area,industry,list_date')
data = pd.concat([data, pro.stock_basic(exchange='', market = "创业板", list_status='', fields='ts_code,symbol,name,area,industry,list_date')], axis=0, ignore_index=True)
data = pd.concat([data, pro.stock_basic(exchange='', market = "科创板", list_status='', fields='ts_code,symbol,name,area,industry,list_date')], axis=0, ignore_index=True)

通过总市值除以净利润计算PE指标，如公式[1]：

$PE = \frac{Price}{EPS}=\frac{Price\times no.\, \, shares}{EPS \times no.\, \, shares} = \frac{MV}{NI}\, \, \, [1]$

Tushare接口对数据请求频率有要求，下面请求数据时需要进行0.3秒左右的休眠。

1）净利润：遍历所有公司，先获取财务数据，把所有公司的净利润数据合并到一张大表里。笔者发现Tushare的数据有些日期格式比较乱，下面还需要对数据进行简单清洗：

income_stat = pd.DataFrame()

for i in range(len(data["ts_code"])):
    code = data["ts_code"][i]
    df = pro.income(ts_code=code, start_date='20050101', end_date='20231001', fields='ts_code,end_date,n_income')[::-1]
    df.drop_duplicates("end_date", inplace=True)
    df.set_index("end_date", inplace=True)
    df.columns = df.columns.str.replace("n_income", code)
    
    income_stat = pd.concat([income_stat, df[code]], axis = 1)
    print("已完成{}%\r".format('%.3f'%(100*(1+i)/len(data["ts_code"]))), end="")
    time.sleep(0.3)
    
# 日期排序
income_stat["date"] = income_stat.index
income_stat["date"] = income_stat["date"].astype("int")
income_stat = income_stat.sort_values("date")
income_stat = income_stat.loc[:, ~(income_stat.columns == "date")]
# 清洗数据
income_stat = income_stat[~(income_stat.apply(lambda x: x.sum(), axis=1)==0)]
income_stat = income_stat[~(income_stat.index == "20170131")]

这里需要说明一点，受限于数据库字段，财务数据笔者是直接按照财务报告期进行计算的，这样也方便统一合并表格，实际上要等到次年3月或4月份公司发布财报才能拿到去年的年报数据。但笔者认为这对结果不会造成重大影响，并且通过剔除负值的指标接口获取的PE数据最后计算出来的走势也可以印证（接口直接获取的PE也好PE TTM也好，都是实际的数值，不存在什么前视偏差）。

2）市值：

mv_lst = []
code_lst = []
for code in data["ts_code"]:
    df = pro.daily_basic(ts_code=code, start_date='20050101', end_date='20231001', fields='ts_code,trade_date,total_mv')[::-1]
    df.set_index("trade_date", inplace=True)
    code_lst.append(code)
    mv_lst.append(df["total_mv"])
    print("进度：{}, 第{}家, 完成{}%\r".format(code, len(code_lst), ('%.2f'%(100*len(code_lst)/ len(data)))), end="")
    time.sleep(0.29)

接下来对金融板块进行剔除，计算市值权重占比。金融板块笔者选择的是银行和非银金融：

financial_sector = pro.index_member(index_code='801780.SI')
financial_sector = pd.concat([financial_sector, pro.index_member(index_code='801790.SI')], axis=0, ignore_index=True)
financial_codes = financial_sector["con_code"].values

mv_table = pd.concat(mv_lst, axis=1)
mv_table = mv_table.sort_values("trade_date")
mv_table.columns = code_lst

sub_mv_table = mv_table.copy()
for i in financial_codes: ## 剔除金融
    sub_mv_table = sub_mv_table.loc[:, sub_mv_table.columns != i]
     
sum_mv = sub_mv_table.apply(lambda x: x.sum(), axis = 1)
i = 1
mv_weigths = []
column_lst = []
for col in sub_mv_table:##计算权重
    mv_weigths.append(sub_mv_table[col] / sum_mv)
    column_lst.append(col)
    print("进度：{}%\r".format(('%.2f'%(100*i/ len(sub_mv_table.columns)))), end="")
    i += 1
mv_weigths = pd.concat(mv_weigths, axis=1)
mv_weigths.columns = column_lst

下面计算PE指标数据：

dates = income_stat.index.to_list()
dates.append("20231001")

pe_table = pd.DataFrame()
sub_income_stat = income_stat.copy()
for i in financial_codes:
    sub_income_stat = sub_income_stat.loc[:, sub_income_stat.columns != i]

i = 1
sub_income_stat = sub_income_stat.rolling(4).sum() ## 过去四个月算总和，其实TTM算平均也可以，但是都不会影响后面分位数计算
for col in sub_income_stat.columns:
    pe = []
    for date in range(len(dates)-1):
        start = dates[date]
        end = dates[date+1]
        ni = sub_income_stat.loc[start, col]/10000
        lst = mv_table.loc[((mv_table.index > start) & (mv_table.index <= end)), col] / ni
        pe.append(lst)
    pe = pd.concat(pe, axis=0)
    pe.columns = [col]
    pe_table = pd.concat([pe_table, pe], axis = 1)
    print("进度：{}%\r".format(('%.2f'%(i*100/len(sub_income_stat.columns)))), end="")
    i += 1

有PE数据后还不够，还需要把这些数据转换成分位数，这里笔者写了两个模块进行调用：

def percentail_mod(series):
    pctail = []
    for row in series.index[10:]:
        sub_series = series[:row].copy()
        pct = len(sub_series[sub_series<series[row]])/len(sub_series)
        date = row
        pctail.append({"date": date, "pctail": pct})
    pctail = pd.DataFrame(pctail)
    pctail.set_index("date", inplace=True) ## 设置索引，方便后面按索引合并表格
    return pctail


def pctail_table_mod(df, financial_codes):
    data = pd.DataFrame() ## 建立分位数存储表格
    data.index = df.index ## 设置索引，方便后面按索引合并
    col_names = []
    i = 1
    for col in df.columns:
        series = df[col].dropna() ## 去掉Nan不然影响分位数计算
        if len(series) > 30: ## 数据太少不看
            series = series[20:] ## 刚上市一个月的不看了
            pctail = percentail_mod(series) ## 调用模块计算分位值

            data = pd.concat([data, pctail], axis=1)
            col_names.append(col)
            print("已完成{}%\r".format(('%.2f'%(100*(1+i)/(len(df.columns))))), end="")
        else:
            pass
        i += 1
    data.columns = col_names ## 要把列名改过来，否则所有列都会叫pctail
    return data


pe_pctail_table = pctail_table_mod(pe_table, financial_codes)

数据都准备好了，下面只需要进行全市场估值分位数计算即可：

weighted_pe_pctail_table = []
for col in pe_pctail_table:
    weighted_pe_pctail_table.append(pe_pctail_table[col] * mv_weigths[col])
    
weighted_pe_pctail_table = pd.concat(weighted_pe_pctail_table, axis=1)
index_pctail = weighted_pe_pctail_table.apply(lambda x: x.sum(), axis = 1)
index_pctail = index_pctail[index_pctail.index > "20060101"] ## 净利润是TTM数据，2005年四个季度的数据舍去，从06年开始

最后运行可视化即可得到图三：

plt.figure(figsize=(16,8))
plt.plot(index_pctail.index.values, index_pctail.values*100, label="加权PE_ttm分位数, 剔除金融板块")
plt.plot(index_pctail.index.values, [(index_pctail.values*100).mean()]*len(index_pctail.index.values), linestyle="--", label="均值")
plt.plot(index_pctail.index.values, [(index_pctail.values*100).std()+(index_pctail.values*100).mean()]*len(index_pctail.index.values), linestyle="-.", label="+/-1标准差")
plt.plot(index_pctail.index.values, [(index_pctail.values*100).mean()-(index_pctail.values*100).std()]*len(index_pctail.index.values), linestyle="-.", color="g")
plt.xticks(index_pctail.index.values[::125], rotation=45, size=15)
plt.yticks(size=15)
plt.xlabel("日期", size=18)
plt.ylabel("加权平均分位点(%)", size=18)
plt.title("A股非金融加权PE_ttm分位数", size=22)
plt.legend(fontsize=15)
plt.show()

如法炮制也可以计算PB，以及剔除负值后的估值，这里就不展示了。

5.2 整体法PE

使用上面获取到的数据还可以用整体法算，只要把金融板块剔除的代码改改就可以变成全市场的整体法PE TTM结果：

sub_mv_table = mv_table.copy()
for i in financial_codes: ## 对金融板块进行剔除
    sub_mv_table = sub_mv_table.loc[:, sub_mv_table.columns != i]
    
sub_income_stat = income_stat.copy()
for i in financial_codes: ## 对金融板块进行剔除
    sub_income_stat = sub_income_stat.loc[:, sub_income_stat.columns != i]
    
sum_mv = sub_mv_table.apply(lambda x: x.sum(), axis=1)
sub_income_stat = sub_income_stat.rolling(4).mean()
sum_income_stat = sub_income_stat.apply(lambda x: x.sum(), axis=1)

dates = income_stat.index.to_list()
dates.append("20231001")
i = 1
index_lst = []
for date in range(len(dates)-1):
    start = dates[date]
    end = dates[date+1]
    ni = sum_income_stat[start]/10000 # Tushare市值的单位是万，这里除掉后与市值单位保持一致
    lst = sum_mv[((sum_mv.index > start) & (sum_mv.index <= end))] / ni
    index_lst.append(lst)
    print("进度：{}%\r".format(('%.2f'%((1+i)*100/len(dates)))), end="")
    i += 1
    
index_lst = pd.concat(index_lst, axis=0)
index_lst = index_lst[index_lst.index >= "20060101"]
plt.figure(figsize=(10,5))

index_lst.plot()
plt.xticks(rotation=45)
plt.xlabel("日期", size=15)
plt.ylabel("PE", size=15)
plt.title("A股PE ttm（整体法）", size=15)
plt.show()

5.3 行业分位数法估值重构

下面以通信行业为例，其实主要代码主体和上面全市场的计算代码是类似的，只是把公司代码列表换成通信行业的，笔者就不进行更多讲解了：

# 获取数据
sector = pro.index_member(index_code='801770.SI')
income_stat = pd.DataFrame()
for row in range(len(sector)):
    in_date = sector.loc[row, "in_date"]
    out_date = sector.loc[row, "out_date"]
    code = sector.loc[row, "con_code"]
    df = pro.income(ts_code=code, start_date=in_date, end_date=out_date, fields='ts_code,end_date,n_income')[::-1]
    df.drop_duplicates("end_date", inplace=True)
    df.set_index("end_date", inplace=True)
    df.columns = df.columns.str.replace("n_income", code)
    
    income_stat = pd.concat([income_stat, df[code]], axis = 1)
    print("已完成{}%\r".format('%.3f'%(100*(1+row)/len(sector))), end="")
    time.sleep(0.3)
    

# 清洗数据
income_stat = income_stat[~(income_stat.apply(lambda x: x.sum(), axis=1)==0)]
income_stat = income_stat[~(income_stat.index == "20170131")]
income_stat = income_stat.rolling(4).sum()
income_stat.dropna(how="all", axis=0, inplace=True)

mv_lst = []
code_lst = []
for code in tc_codes:
    df = pro.daily_basic(ts_code=code, start_date='20050101', end_date='20231001', fields='ts_code,trade_date,total_mv')[::-1]
    df.set_index("trade_date", inplace=True)
    code_lst.append(code)
    mv_lst.append(df["total_mv"])
    print("进度：{}, 第{}家, 完成{}%\r".format(code, len(code_lst), ('%.2f'%(100*len(code_lst)/ len(tc_codes)))), end="")
    time.sleep(0.298)


# 处理数据，合并、清洗
mv_table = pd.concat(mv_lst, axis=1)
mv_table = mv_table.sort_values("trade_date")
mv_table.columns = code_lst
mv_table = mv_table.loc[:, ~(mv_table.columns.duplicated())]

sum_mv = mv_table.apply(lambda x: x.sum(), axis = 1)
i = 1
mv_weights = []
column_lst = []
for col in mv_table:
    mv_weights.append(mv_table[col] / sum_mv)
    column_lst.append(col)
    print("MV进度：{}%\r".format(('%.2f'%(100*i/ len(mv_table.columns)))), end="")
    i += 1
mv_weights = pd.concat(mv_weights, axis=1)
mv_weights.columns = column_lst


# 指标计算
print("\n")
dates = income_stat.index.sort_values().tolist()
dates.append("20231001")
pe_table = pd.DataFrame()
i = 1
income_stat = income_stat.loc[:, ~(income_stat.columns.duplicated())]
for col in income_stat.columns:
    pe = []
    for date in range(len(dates)-1):
        start = dates[date]
        end = dates[date+1]
        ni = income_stat.loc[start, col]/10000
        lst = mv_table.loc[((mv_table.index > start) & (mv_table.index <= end)), col] / ni
        pe.append(lst)
    pe = pd.concat(pe, axis=0)
    pe.columns = [col]
    pe_table = pd.concat([pe_table, pe], axis = 1)
    print("PE进度：{}%\r".format(('%.2f'%(i*100/len(income_stat.columns)))), end="")
    i += 1

pe_pctail_table = pctail_table_mod(pe_table)
weighted_pe_pctail_table = []
for col in pe_pctail_table:
    weighted_pe_pctail_table.append(pe_pctail_table[col] * mv_weights[col])
    
weighted_pe_pctail_table = pd.concat(weighted_pe_pctail_table, axis=1)
weighted_pe_pctail_table = weighted_pe_pctail_table.dropna(how = "all", axis = 0)
index_pctail = weighted_pe_pctail_table.apply(lambda x: x.sum(), axis = 1)


# 可视化
plt.figure(figsize=(16,8))
plt.plot(index_pctail.index.values, index_pctail.values*100, label="加权PE_ttm分位数")
plt.plot(index_pctail.index.values, [(index_pctail.values*100).mean()]*len(index_pctail.index.values), linestyle="--", label="均值")
plt.plot(index_pctail.index.values, [(index_pctail.values*100).std()+(index_pctail.values*100).mean()]*len(index_pctail.index.values), linestyle="-.", label="+/-1标准差")
plt.plot(index_pctail.index.values, [(index_pctail.values*100).mean()-(index_pctail.values*100).std()]*len(index_pctail.index.values), linestyle="-.", color="g")
plt.xticks(index_pctail.index.values[::125], rotation=45, size=15)
plt.yticks(size=15)
plt.xlabel("日期", size=18)
plt.ylabel("加权平均分位点(%)", size=18)
plt.title("通信行业加权PE_ttm分位数", size=18)
plt.legend(fontsize=15)
plt.show()

以上代码计算出来的是包含负值的PE，其实通过Tushare接口获取的PE是剔除负值的，过程也很简单，笔者也不进行展示了，前文的图八和图九两个行业就是使用剔除负值计算的结果。

策略实现相关代码笔者就不放了，行文至此已一万三千余字了。

6. 总结

本期笔者对指数及行业进行了分位数法的重构，由于研报写得也比较简略，一些数据选取范围和参数设置并未披露，笔者也并未完全复现出研报中的结果。本文还对申万31个一级行业进行了重估，从截面数据的角度解读重估值数据的使用方式。最后，笔者通过重估后的估值数据设计相关策略，策略结果并没有显示出重估后的数据比原始数据有更强指导意义，但该结果只是回测结论，笔者认为分位数法的重构是个不错的思路和方法，在实践中存在一定的意义。

7. 引用

【1】：曹柳龙，2023.09.07，方正证券，P1-13, "方正证券-行业比较“新视界”系列报告（二）：如何打破“估值幻觉”？"

8. 往期精选

往期精选
系列	文章传送门	实现方式
权益投资	PB指标与剩余收益估值	Python
	Fama-French及PSM	Python
	GK模型看投资的本质	Python
	增速g的测算	Python
	PE指标平滑	Python
	PE Band	Python
	分类树算法	R
	蒙特卡洛模拟	Python
	全连接神经网络模型	Python
杂谈类	券商金股哪家强——信息比率	Python
	从指数构建原理看待A股的三千点魔咒	Python
	决策树学习基金持仓并识别公司风格类型	R
	垃圾公司对回报率计算的影响几何	Python
	市场预测美联储加息的有效性几何	Python
	市场风险分析	Python