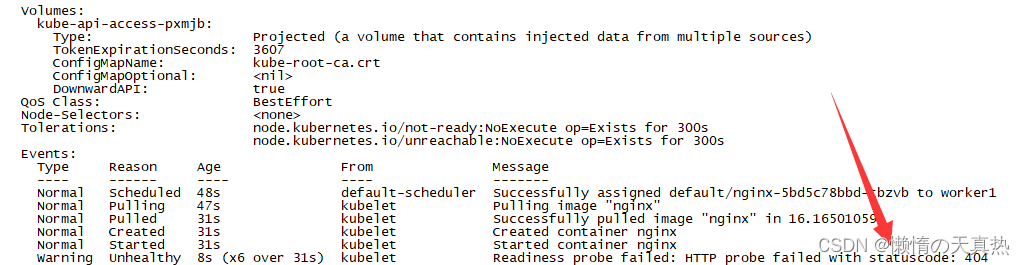
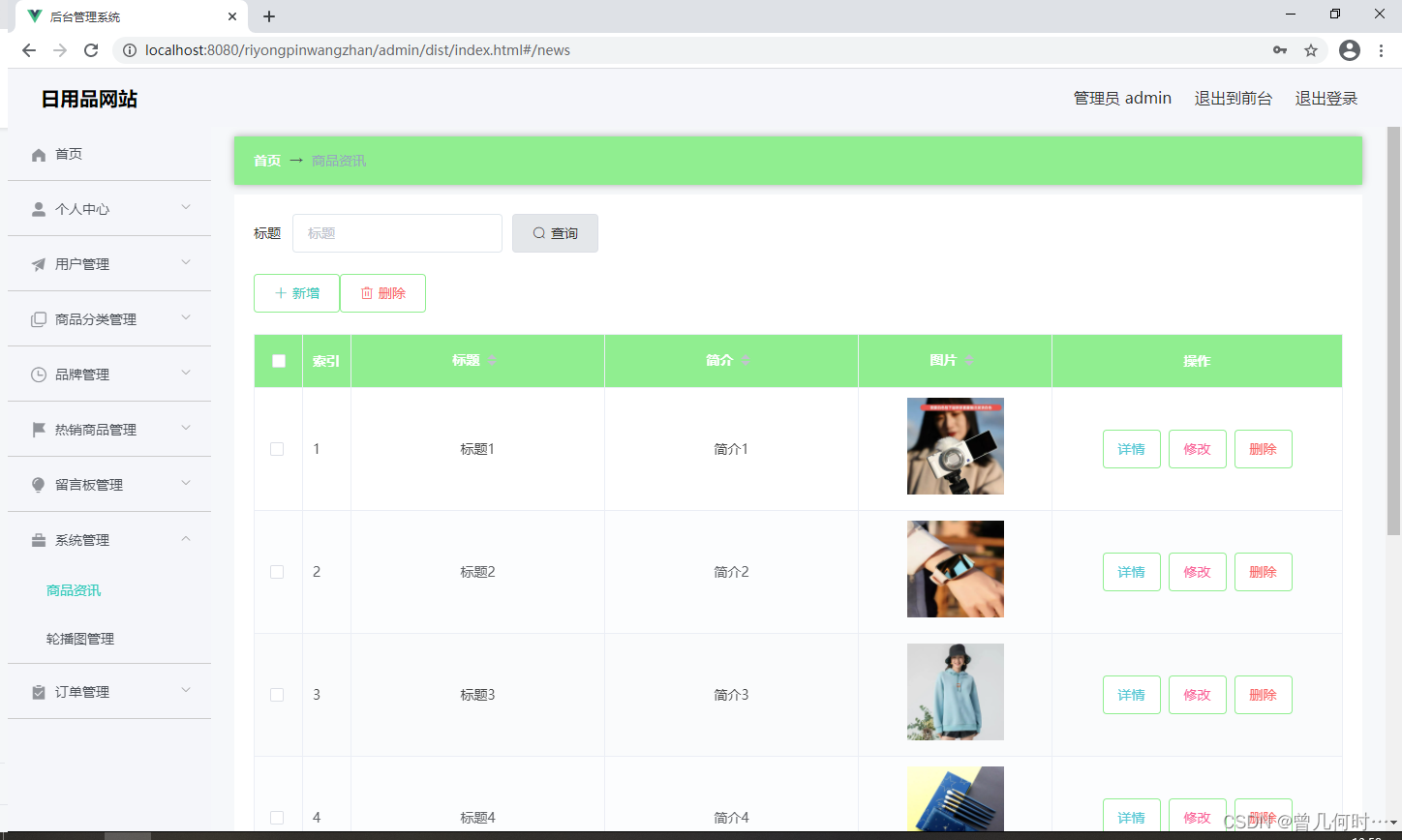
import optimtool as oo
from optimtool.base import np, sp, plt

pip install optimtool # any version with accessible L_BFGS 

加载L_BFGS方法

import optimtool.unconstrain as ou
lbfgs = ou.newton_quasi.L_BFGS

$$f(x)=\sum _{i=1}^{n-1}(x_i+x_{i+1}-3{)}^2+(x_i-x_{i+1}+1{)}^4,x_0=[2,2,...,2].$$

初始化输入数据

# make data(3 dimension)
x = sp.symbols("x1:4")
f = (x[0] + x[1] - 3)**2 + (x[0] - x[1] + 1)**4 + \
    (x[1] + x[2] - 3)**2 + (x[1] - x[2] + 1)**4
x_0 = (2, 2, 2) # Random given

查看L_BFGS超参数

L_BFGS(funcs: FuncArray, args: ArgArray, x_0: PointArray, verbose: bool=False, draw: bool=True, output_f: bool=False, method: str=“wolfe”, m: float=6, epsilon: float=1e-10, k: int=0) -> OutputType

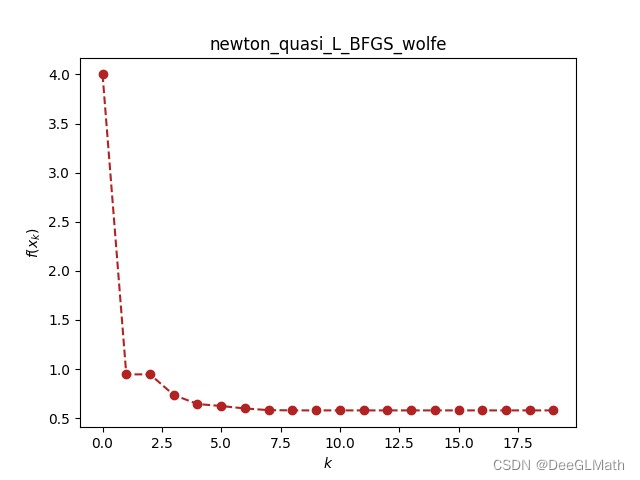
调用并绘制迭代图

print(lbfgs(f, x, x_0, verbose=True))

(2, 2, 2)       4.0     0
[1.25 1.5  2.25]        0.9453125000000002      1
[1.2508132  1.50055287 2.24971504]      0.9455254266849167      2
[1.14857133 1.53464418 2.15242661]      0.7358195964077977      3
[1.08514444 1.59724704 2.00578909]      0.6435684144202295      4
[1.04712651 1.55941861 2.00256007]      0.6233603758928477      5
[1.02980813 1.5177135  1.95872827]      0.5981377885052529      6
[1.06143634 1.49410798 1.92206387]      0.5814170599663506      7
[1.08729744 1.49657415 1.90815247]      0.5786175770124571      8
[1.08940649 1.4996921  1.9096457 ]      0.5785482832298223      9
[1.08979309 1.49998871 1.91028685]      0.5785468604986556      10
[1.08975568 1.49999224 1.91024822]      0.5785468483400542      11
[1.08975376 1.49999833 1.9102448 ]      0.578546847890699       12
[1.08975434 1.49999989 1.91024533]      0.5785468478757178      13
[1.0897545  1.5        1.91024548]      0.5785468478755569      14
[1.08975451 1.5        1.91024549]      0.5785468478755555      15
[1.08975451 1.5        1.91024549]      0.578546847875556       16
[1.08975451 1.5        1.91024549]      0.5785468478755558      17
[1.08975451 1.5        1.91024549]      0.5785468478755561      18
[1.08975451 1.5        1.91024549]      0.5785468478755559      19