文章目录
-
- 第一部分:矩阵
- 第一部分习题
- 第二部分:对称矩阵
- 第二部分习题
- 第三部分:三角矩阵
- 第三部分习题
- 第四部分:三对角矩阵
- 第四部分习题
- 第五部分:稀疏矩阵
- 第五部分习题
- 小结
第一部分:矩阵
矩阵在线性代数中已经有过详细了解,在考研中矩阵部分常常考察数组下标 k 与 矩阵行 i 和列 j 的关系。
需要注意的是矩阵下标 i、j 通常是: 1 到 n 1到n 1到n,而数组下标 k 通常是: 0 到 n 2 − 1 0到n^2-1 0到n2−1。
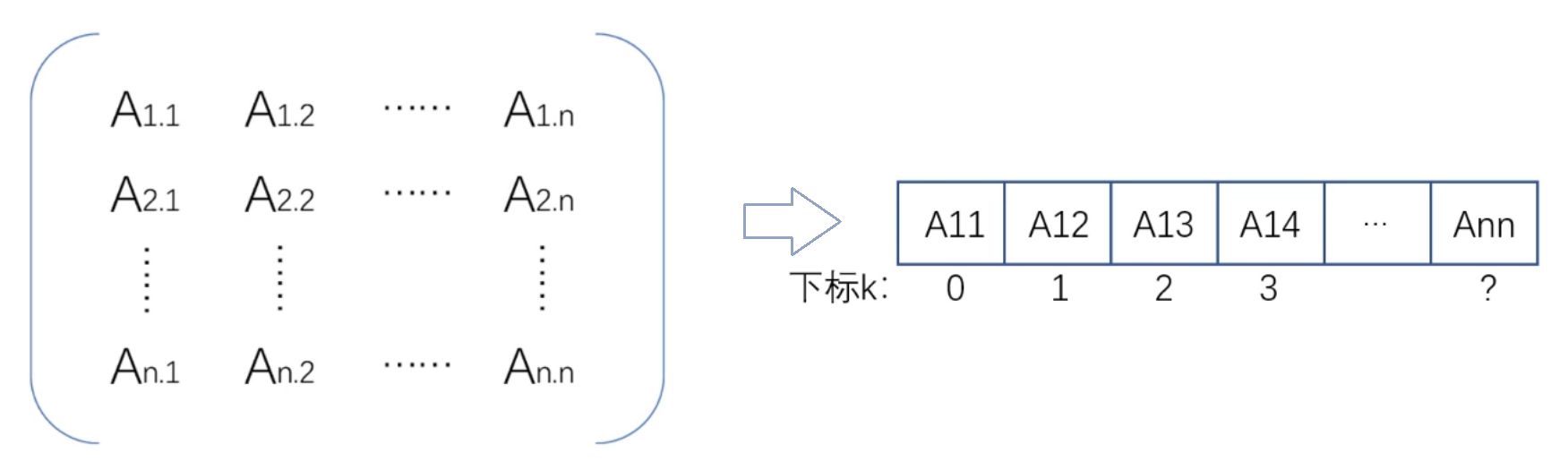
- k 与 i、j 的关系就是: k = n ∗ ( i − 1 ) + j − 1 k=n*(i-1)+j-1 k=n∗(i−1)+j−1
第一部分习题
- 数组A中,每个元素的长度为3个字节,行下标 i 从1到8,列下标 j 从1到10,从首地址SA开始连续存放的存储器内,该数组按行存放,元素 A[8][5] 的起始地址为(C)。
A.SA+141
B.SA+144
C.SA+222(用公式可以求出 A 85 A_{85} A85前面有74个元素,所以它的起始地址就是: S A + 74 ∗ 3 SA+74*3 SA+74∗3)
D.SA+225 - 设二维数组 A[1…m,1…n] 按行存储在数组B中,则二维数组元素 A[i,j] 在一维数组B中的下标为(A)。
A.n*(i-1)+j(题目中没有强调数组B的下标从0开始,再结合其他选项只能选A)
B.n*(i-1)-j-1(迷惑性选项,“- j”必然是错的)
C.i*(j-1)
D.i*m+i-1
第二部分:对称矩阵
对称矩阵就是主对角线两侧的数据相同的方阵,对于这类矩阵我们通常可以节约空间,只存储上三角部分的数据或下三角部分的数据。
- 此时数组下标 k 与 矩阵行 i 和列 j 的关系通常满足(上三角转置后就是下三角了): k 下三角 = S i − 1 + j − 1 k 上三角 = S j − 1 + i − 1 k_{下三角}=S_{i-1}+j-1\\k_{上三角}=S_{j-1}+i-1 k下三角=Si−1+