链接：卡码网KamaCoder

题目：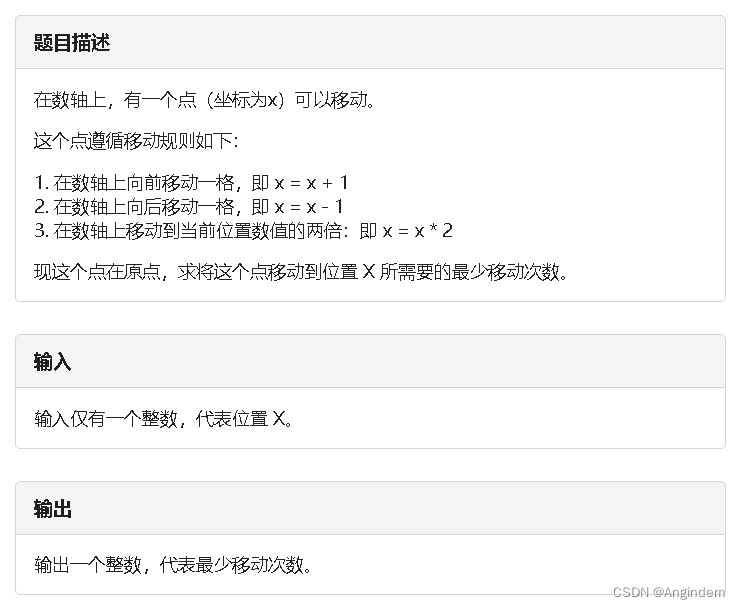

样例：

3

思路：

        这道题是求最少步数，联想一下 BFS，BFS 操作可得

这是一个正向的 BFS

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
using PII = pair<int, int>;

int n;

umap<int, bool>st;	// 标记是否到达过的结点

// 三个操作的遍历
inline void op(queue<int>&q,int &now)
{
	if (!st[now + 1])
	{
		st[now + 1] = true;
		q.emplace(now + 1);
	}
	if (!st[now - 1])
	{
		st[now - 1] = true;
		q.emplace(now - 1);
	}
	if (!st[now << 1])
	{
		st[now << 1] = true;
		q.emplace(now << 1);
	}
}

inline int BFS()
{
	int step = 0;
	queue<int>q;	// 建立队列
	q.emplace(0);	// 存储起点

	while (q.size())
	{
		int sz = q.size();
		while (sz--)
		{
			int now = q.front();	// 取出当前结点
			q.pop();

			st[now] = true;	// 标记当前结点

			if (now == n)
				return step;	// 如果到达了终点返回步数

			// 遍历三个操作
			op(q,now);
		}
		++step;	// 步数累加
	}
	return -1;	// 给定一个最终结果
}

inline void solve()
{
	cin >> n;
	cout << BFS() << endl;
}

signed main()
{
//	freopen("a.txt", "r", stdin);
	___G;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

提交后我们可以发现：

内存超限了部分测试数据，关键点在于   操作 3 中 x = x * 2 使得 当某个数值的时候 ，使用操作3后，有可能 x > n 不必要的数据存储在了 q 中，这就是正向 BFS 的一个小缺陷

我们可以试一下 反向BFS，以 终点 为起步存储点，往 0 方向操作，此时  now 应该被整除的时候，是最佳最少步数方案的，这样可以 避免 x = x * 2 中  x > n 的数据，节省了部分空间。

代码详解如下：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
using PII = pair<int, int>;

int n;

umap<int, bool>st;	// 标记是否到达过的结点

// 三个操作的遍历
inline void op(queue<int>&q,int &now)
{
	if (!st[now + 1])
	{
		st[now + 1] = true;
		q.emplace(now + 1);
	}
	if (!st[now - 1])
	{
		st[now - 1] = true;
		q.emplace(now - 1);
	}
	
	// 操作 3 中往 0 方向 走
	if (now % 2 == 0 && !st[now >> 1] )
	{
		st[now >> 1] = true;
		q.emplace(now >> 1);
	}
}

inline int BFS()
{
	int step = 0;
	queue<int>q;	// 建立队列
	
	q.emplace(n);	// 存储起点，  将 n 作为起点

	while (q.size())
	{
		int sz = q.size();
		while (sz--)
		{
			int now = q.front();	// 取出当前结点
			q.pop();

			st[now] = true;	// 标记当前结点

			if (!now)
				return step;	// 如果到达了起点返回步数

			// 遍历三个操作
			op(q,now);
		}
		++step;	// 步数累加
	}
	return -1;	// 给定一个最终结果
}

inline void solve()
{
	cin >> n;
	cout << BFS() << endl;
}

signed main()
{
//	freopen("a.txt", "r", stdin);
	___G;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：