给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

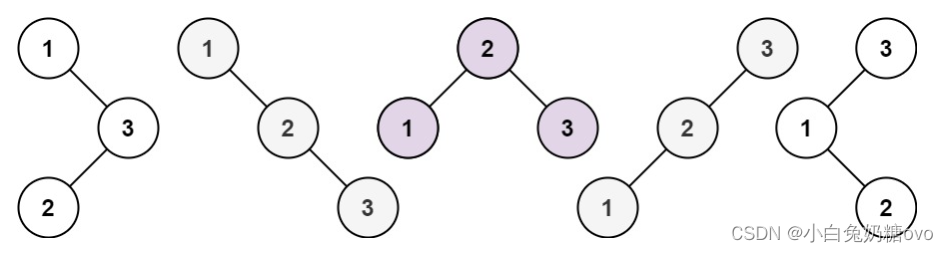
示例 1：

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：
1 <= n <= 19

---

AC:

/*
 * @lc app=leetcode.cn id=96 lang=cpp
 *
 * [96] 不同的二叉搜索树
 */

// @lc code=start
class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;
        dp[1] = 0;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};
// @lc code=end

在这段代码中，dp[0] 被初始化为 1，而不是 dp[1]。这是因为在计算二叉搜索树的数量时，当节点数为0时，只有一种情况，即空树。因此，dp[0] 的值应该为 1。

如果将 dp[1] 直接初始化为 1，那么在计算节点数为 1 的二叉搜索树数量时，会出现错误。因为当节点数为 1 时，只有一个节点，无法构成二叉搜索树。因此，dp[1] 的值应该为 0。

在这段代码中，dp[0] 被初始化为 1，是为了方便计算。在计算节点数为 i 的二叉搜索树数量时，需要遍历所有可能的左子树和右子树，因此需要从 dp[0] 开始计算。如果将 dp[0] 初始化为 0，那么在计算节点数为 2 的二叉搜索树数量时，需要使用 dp[1] 的值，而 dp[1] 的值为 0，会导致计算错误。

因此，将 dp[0] 初始化为 1，可以避免这个问题，同时也方便了计算。

---

同时，如果不初始化dp[1]，该代码也是可以AC的！

/*
 * @lc app=leetcode.cn id=96 lang=cpp
 *
 * [96] 不同的二叉搜索树
 */

// @lc code=start
class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};
// @lc code=end

---