一、问题背景
N皇后问题是由八皇后问题引申而来的。八皇后是一个以国际象棋为背景的问题,国际象棋8*8.
怎么去放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
条件n = 1或n ≥ 4
二、算法介绍
此题解的算法使用的是:回溯法(Backtracking)
回溯法是暴力搜索法里的一种。其核心是通过逐步构建空间,并在构建过程中进行选择、判断和回退,直到找到问题的解或者确定不存在解。
回溯法采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现,现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
- 找到一个可能存在的正确的答案
- 在尝试了所有可能的分步方法后宣告该问题没有答案
回溯法的优点是可以穷尽所有可能的解空间,并找到所有满足条件的解。但同时,由于它遍历了所有可能的解空间,所以在解空间很大的情况下,会产生指数级的时间复杂度,因此效率可能较低。
回溯法的经典应用包括:N皇后问题、组合求和、排列组合、子集、正则表达式匹配等。
三、代码示例
1、C语言版本(ACM算法题目里面经典)
#include <stdio.h>
#define N 8 // N代表棋盘的大小,这里设置为8
int board[N][N]; // 棋盘数组,用于表示每个位置是否放置皇后
// 检查当前位置(row, col)是否可以放置皇后
int isSafe(int row, int col) {
int i, j;
// 检查当前列是否有皇后冲突
for (i = 0; i < row; i++) {
if (board[i][col] == 1) {
return 0;
}
}
// 检查当前位置的左上方是否有皇后冲突
for (i = row, j = col; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 1) {
return 0;
}
}
// 检查当前位置的右上方是否有皇后冲突
for (i = row, j = col; i >= 0 && j < N; i--, j++) {
if (board[i][j] == 1) {
return 0;
}
}
return 1; // 当前位置可以放置皇后
}
// 使用回溯法解决N皇后问题
int solveNQueens(int row) {
if (row == N) {
// 打印解
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
printf("%d ", board[i][j]);
}
printf("\n");
}
printf("\n");
// 只打印一个解的话,可以使用 return 1; 终止程序
// return 1;
}
for (int col = 0; col < N; col++) {
if (isSafe(row, col)) {
// 当前位置可以放置皇后
board[row][col] = 1;
// 递归调用解决下一行
solveNQueens(row + 1);
// 回溯,撤销当前位置的选择
board[row][col] = 0;
}
}
return 0; // 所有解都已找到
}
int main() {
solveNQueens(0); // 从第一行开始解决N皇后问题
return 0;
}2、JS版本 (主要是思想)
function solveNQueens(n) {
// 存储结果的数组
let result = [];
// 执行回溯算法
backtrack([], [], [], result, n);
// 返回结果数组
return result;
}
// 回溯函数
function backtrack(board, cols, diagonals1, diagonals2, n) {
// 当前棋盘的大小等于N时,表示已找到一种解法,将其存入结果数组
if (board.length === n) {
result.push(board.slice());
return;
}
// 遍历当前行的每一列
for (let col = 0; col < n; col++) {
// 当前格子的行索引
let row = board.length;
// 根据皇后的摆放规则判断当前位置是否可行
if (
!cols.includes(col) && // 列上无冲突
!diagonals1.includes(row - col) && // 主对角线无冲突
!diagonals2.includes(row + col) // 副对角线无冲突
) {
// 将当前位置加入相应的集合中,表示皇后占据了该位置
board.push(col);
cols.push(col);
diagonals1.push(row - col);
diagonals2.push(row + col);
// 继续递归搜索下一行
backtrack(board, cols, diagonals1, diagonals2, n);
// 搜索完之后,将当前位置从集合中移除,以便进行下一次搜索
board.pop();
cols.pop();
diagonals1.pop();
diagonals2.pop();
}
}
}
// 通过维护cols、diagonals1和diagonals2三个集合,来判断当前位置是否符合皇后的放置规则。
// 如果找到一种解法,将其存入结果数组中,并继续搜索下一行的解法。
// 在搜索完一条路径之后,需要将当前位置从集合中移除,以便进行下一次搜索。四、结果
八皇后:12个解
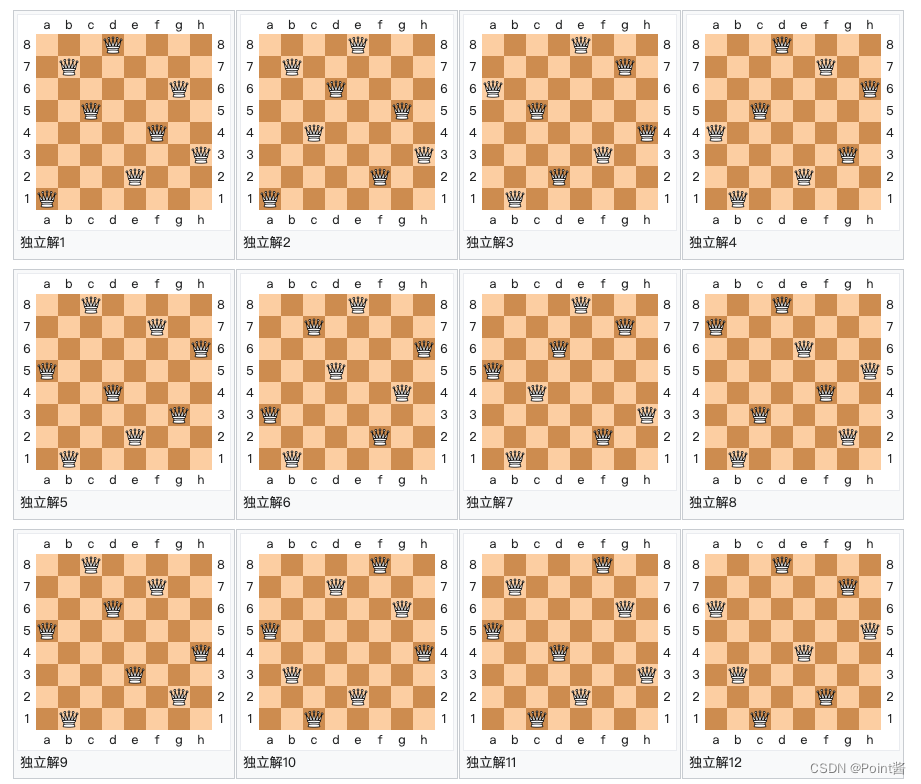
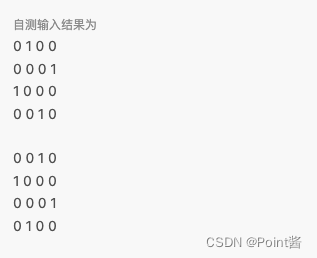
四皇后:2个解
(1,3,0,2)
(2,0,3,1)