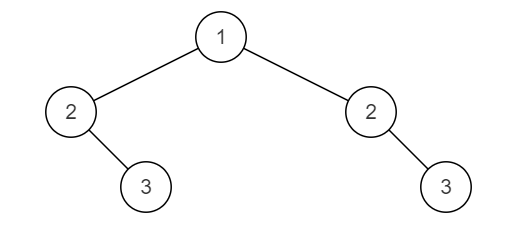
二叉树的最小深度

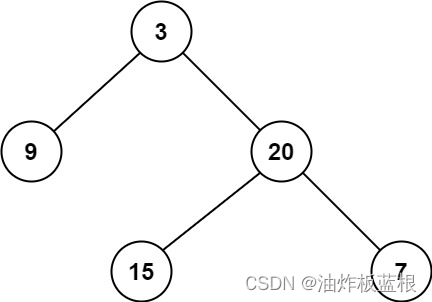
给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

思路

这道题本质上是考察：

1. 如何遍历二叉树
2. 理解什么是深度

对于这两点的考察，其实最底层的思路还是要对数据结构有灵活的应用；很明显，最小的二叉树深度就是广度遍历二叉树的时候，找到深度最小的叶子结点。我们只需要一层一层的遍历，只要找到叶子节点，返回它的深度就行了。

use std::cell::RefCell;
use std::ops::Not;
use std::rc::Rc;
use crate::solution::Solution;
use crate::tree_node::TreeNode;

impl Solution {
    //  给定一个二叉树，找到其最小深度
    pub fn min_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        if root.is_none() {
            return 0;
        }
        let mut queue = Vec::new();
        queue.push(root.unwrap());
        let mut result = 1;
        while !queue.is_empty() {
            let queue_len = queue.len();
            for _ in 0..queue_len {
                let node = queue.remove(0);
                if node.borrow().left.is_none() && node.borrow().right.is_none() {
                    return result;
                }
                if node.borrow().left.is_some(){
                    queue.push(node.borrow_mut().left.take().unwrap());
                }
                if node.borrow().right.is_some(){
                    queue.push(node.borrow_mut().right.take().unwrap());
                }
            }
            result += 1;
        }
        return result;
    }
}

该处使用了非递归的广度优先遍历。稍微使用了一个比较巧妙的方法，每次都把某层的节点推入到队列中，并且记录该层有多少个节点，然后根据记录的个数，取出该层的节点去判断。