暴力递归到动态规划(三)
- 最长公共子序列
- 递归版本
- 动态规划
- 最长回文串子序列
- 方法一
- 方法二
- 递归版本
- 动态规划
- 象棋问题
- 递归版本
- 动态规划
- 咖啡机问题
- 递归版本
- 动态规划
最长公共子序列
这是leetcode上的一道原题 题目连接如下
最长公共子序列
题目描述如下
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
递归版本
还是一样 我们首先来设计一个函数 函数原型如下
int process(string& str1 , string& str2 , int i , int j)
这个递归函数的含义是 给你两个字符串 s1 和 s2 再给你它们的一个最大下标 现在要求这个函数返回它们公共子序列的最大值
参数表示如下
- int i : 表示一个字符串str1中的下标
- int j : 表示一个字符串str2中的下标
还是一样 我们首先想base case
- 假如i的下标为0 j的下标也为0 此时我们就可以直接返回一个确定的值
代码表示如下
// base case
if (i == 0 && j == 0)
{
return str1[i] == str2[j] ? 1 : 0;
}
此时我们排除了i 和 j都为0的情况 剩下了三种情况
- i j 其中一个为0 (两种)
- i j都不为0
当i j都不为0时候 我们还要讨论 i j 是否为公共子序列的下标也是分为三种情况
- i可能是 j不是
- j可能是 i不是
- i j都是
之后我们分别将代码全部写好就可以了
if (i == 0)
{
if (str1[i] == str2[j])
{
return 1;
}
else
{
return process(str1 , str2 , i , j-1);
}
}
else if (j == 0)
{
if (str1[i] == str2[j])
{
return 1;
}
else
{
return process(str1 , str2 , i - 1 , j);
}
}
else
{
// j != 0;
// i != 0;
// possible i ... j
int p1 = process(str1 , str2 , i - 1 , j);
int p2 = process(str1 , str2 , i , j - 1);
int p3 = str1[i] == str2[j] ? 1 + process(str1 , str2 , i -1 , j -1) : 0 ;
return max(p1 , max (p2 , p3));
}
}
动态规划
我们观察原递归函数
process(string& str1 , string& str2 , int i , int j)
我们发现变化的值只有 i 和 j
于是我们可以利用i j 做出一张dp表
还是一样 我们首先来看base case
// base case
if (i == 0 && j == 0)
{
return str1[i] == str2[j] ? 1 : 0;
}
于是我们就可以把i == 0 并且 j ==0 的这些位置值填好
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
之后根据 i == 0 j ==0 这两个分支继续动规
for (int j = 1 ; j < static_cast<int>(str2.size()) ; j++)
{
dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j-1];
}
for (int i = 1 ; i < static_cast<int>(str1.size()) ; i++)
{
dp[i][0] = str1[i] == str2[0] ? 1 : dp[i-1][0];
}
递归的最后一部分依赖三个位置
else
{
// j != 0;
// i != 0;
// possible i ... j
int p1 = process(str1 , str2 , i - 1 , j);
int p2 = process(str1 , str2 , i , j - 1);
int p3 = str1[i] == str2[j] ? 1 + process(str1 , str2 , i -1 , j -1) : 0 ;
return max(p1 , max (p2 , p3));
}
我们只需要再递归表中依次填写即可 代码表示如下
int process1(string& str1, string& str2, vector<vector<int>>& dp)
{
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
for (int j = 1 ; j < static_cast<int>(str2.size()) ; j++)
{
dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j-1];
}
for (int i = 1 ; i < static_cast<int>(str1.size()) ; i++)
{
dp[i][0] = str1[i] == str2[0] ? 1 : dp[i-1][0];
}
for (int i = 1 ; i < static_cast<int>(str1.size()) ; i++)
{
for (int j = 1 ; j < static_cast<int>(str2.size()) ; j++)
{
int p1 = dp[i-1][j];
int p2 = dp[i][j-1];
int p3 = str1[i] == str2[j] ? 1 + dp[i-1][j-1] : 0;
dp[i][j] = max(p1 , max(p2 , p3));
}
}
return dp[str1.size() - 1][str2.size() - 1];
}
最长回文串子序列
方法一
做这道题目我们其实可以复用下上面的最长公共子序列的代码来做
我们可以将字符串逆序一下创造出一个新的字符串
再找出这两个字符串的最长公共子序列 我们找出来的最长公共子序列就是回文子序列 (其实我们可以想想两个指针从一个字符串的两端开始查找)
方法二
递归版本
我们写的递归函数如下
int process(string& str , int L , int R)
它的含义是 我们给定一个字符串str 返回给这个字符串从L到R位置上的最大回文子串
参数含义如下
- str 我们需要知道回文子串长度的字符串
- L 我们需要知道回文子串长度的起始位置
- R 我们需要知道回文子串长度的终止位置
所有的递归函数都一样 我们首先来想base case
这道题目中变化的参数其实就只有L 和 R 所以说我们只需要考虑L和R的base case
如果L和R相等 如果L和R只相差1
if (L == R)
{
return 1;
}
if (L == R - 1)
{
return str[L] == str[R] ? 2 : 1;
}
之后我们来考虑下普遍的可能性
- 如果L 和 R就是回文子序列的一部分
- 如果L可能是回文子序列的一部分 R不是
- 如果L不是回文子序列的一部分 R有可能是
我们按照上面的可能性分析写出下面的代码 之后返回最大值即可
int p1 = process(str , L + 1 , R);
int p2 = process(str , L , R - 1);
int p3 = str[L] == str[R] ? 2 + process(str , L + 1, R - 1) : 0;
return max(max(p1 , p2) , p3);
动态规划
我们注意到原递归函数中 可变参数只有L 和 R 所以说我们只需要围绕着L 和 R建立一张二维表就可以
当然 在一般情况下 L是一定小于等于R的 所以说L大于R的区域我们不考虑
我们首先来看base case
if (L == R)
{
return 1;
}
if (L == R - 1)
{
return str[L] == str[R] ? 2 : 1;
}
围绕着这个base case 我们就可以填写两个对角线的内容
for (int L = 0; L < str.size(); L++)
{
for(int R = L; R < str.size(); R++)
{
if (L == R)
{
dp[L][R] = 0;
}
if (L == R-1)
{
dp[L][R-1] = str[L] == str[R] ? 2 : 1;
}
}
}
接下来我们看一个格子普遍依赖哪些格子
int p1 = process(str , L + 1 , R);
int p2 = process(str , L , R - 1);
int p3 = str[L] == str[R] ? 2 + process(str , L + 1, R - 1) : 0;
从上面的代码我们可以看到 分别依赖于
L+1 R
L , R-1
L+1 , R-1
从图上来分析 黑色的格子依赖于三个红色格子
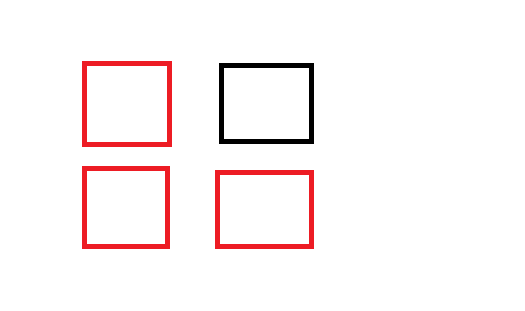
于是我们就可以沿着对角线来不断的填写数字
横行一直从0开始 纵列一直在变化 所以我们用列来遍历
最后返回dp[0][str.size()-1]即可
int process1(string& str , vector<vector<int>>& dp)
{
for (int L = 0; L < str.size(); L++)
{
for(int R = 0; R < str.size(); R++)
{
if (L == R)
{
dp[L][R] = 1;
}
if (L == R-1)
{
dp[L][R] = str[L] == str[R] ? 2 : 1;
}
}
}
for (int startR = 2; startR < str.size(); startR++)
{
int L = 0;
int R = startR;
while (R < str.size())
{
int p1 = dp[L+1][R];
int p2 = dp[L][R-1];
int p3 = str[L] == str[R] ? 2 + dp[L+1][R-1] : 0;
dp[L][R] = max(p1 , max(p2 , p3));
L++;
R++;
}
}
return dp[0][str.size()-1];
}
象棋问题
递归版本
现在给你一个横长为10 纵长为9的棋盘 给你三个参数 x y z
现在一个马从(0 , 0)位置开始运动
提问 有多少种方法使用K步到指定位置 (指定位置坐标随机给出 且一定在棋盘上)
首先我们可以想出这么一个函数
int process(int x , int y , int rest , int a , int b)
它象棋目前在 x y位置 还剩下 rest步 目的地是到 a b位置
让你返回一个最多的路数
我们首先来想base case
- 首先肯定是剩余步数为0 我们要开始判断是否跳到目的地了
- 其次我们还要判断是否越界 如果越界我们直接返回0即可
代码表示如下
if (x < 0 || x > 9 || y < 0 || y > 8)
{
return 0;
}
if (rest == 0)
{
return (x == a && y ==b) ? 1 : 0;
}
接下来我们开始讨论普遍情况 其实就是把马的各个位置跳一遍
int ways = process(x-2 , y+1 , rest-1 , a , b);
ways += process(x-1 , y+2 , rest-1 , a , b);
ways += process(x+1 , y+2 , rest-1 , a , b);
ways += process(x+2 , y+1 , rest-1 , a , b);
ways += process(x-2 , y-1 , rest-1 , a, b);
ways += process(x-1 , y-2 , rest-1 , a , b);
ways += process(x+1 , y-2 , rest-1 , a, b);
ways += process(x+2 , y-1 , rest-1 , a ,b);
其实这样子我们的代码就完成了 总体代码如下
int process(int x , int y , int rest , int a , int b)
{
if (x < 0 || x > 9 || y < 0 || y > 8)
{
return 0;
}
if (rest == 0)
{
return (x == a && y ==b) ? 1 : 0;
}
int ways = process(x-2 , y+1 , rest-1 , a , b);
ways += process(x-1 , y+2 , rest-1 , a , b);
ways += process(x+1 , y+2 , rest-1 , a , b);
ways += process(x+2 , y+1 , rest-1 , a , b);
ways += process(x-2 , y-1 , rest-1 , a, b);
ways += process(x-1 , y-2 , rest-1 , a , b);
ways += process(x+1 , y-2 , rest-1 , a, b);
ways += process(x+2 , y-1 , rest-1 , a ,b);
return ways;
}
动态规划
我们对于原递归函数进行观察 可以得知
int process(int x , int y , int rest , int a , int b)
原函数中 变化的参数只有 x y 和rest 于是乎我们可以建立一个三维的数组
x的范围是0 ~ 9 y的范围是0 ~ 8 而rest的范围则是根据我们步数来决定的 0~K
所以说此时我们以X为横坐标 Y为纵坐标 REST为竖坐标
vector<vector<vector<int>>> dp(10 , vector<vector<int>>(9 , vector<int>(8 , 0)));
我们首先看base case分析下
if (x < 0 || x > 9 || y < 0 || y > 8)
{
return 0;
}
如果有越界的地方 我们直接返回0即可
if (rest == 0)
{
return (x == a && y ==b) ? 1 : 0;
}
在z轴为0的时候 我们只需要将a b 0坐标标记为1即可
nt process1(int k , int a , int b , vector<vector<vector<int>>>& dp)
{
dp[a][b][0] = 1;
for (int z = 1; z <= k; z++)
{
for (int x = 0; x < 10; x++)
{
for (int y = 0; y < 9; y++)
{
int ways = pickdp(x-2 , y+1 , z-1, dp);
ways += pickdp(x-1 , y+2 , z-1 , dp);
ways += pickdp(x+1 , y+2 , z-1 , dp);
ways += pickdp(x+2 , y+1 , z-1 , dp);
ways += pickdp(x-2 , y-1 , z-1 , dp);
ways += pickdp(x-1 , y-2 , z-1 , dp);
ways += pickdp(x+1 , y-2 , z-1 , dp);
ways += pickdp(x+2 , y-1 , z-1 , dp);
dp[x][y][z] = ways;
}
}
}
return dp[0][0][k];
}
咖啡机问题
给你一个数组arr arr[i]表示第i号咖啡机泡一杯咖啡德时间
给定一个正数N 表示第N个人等着咖啡机泡咖啡 每台咖啡机只能轮流泡咖啡
只有一台洗咖啡机 一次只能洗一个被子 时间耗费a 洗完才能洗下一杯
当然 每个咖啡杯也能自己挥发干净 挥发干净的时间为b 咖啡机可以并行的挥发
假设所有人拿到咖啡之后立刻喝干净
返回从开始等待到所有咖啡机变干净的最短时间
我们首先来分析下题目
这里其实是两个问题
- 问题一 每个人喝咖啡喝完的时间是多少
- 问题二 每个人洗完的时间是多少
对于问题一 我们可以使用一个小根堆来做
我们定义一个机器类 里面有两个成员函数
机器的开始时间和机器的使用时间 我们使用它们相加之和来作为小根堆排序的依据
之后我们就能得到每个人喝完咖啡的最优解了
class Machine
{
public:
int _starttime;
int _worktime;
public:
int getsum() const
{
return _starttime + _worktime;
}
public:
Machine() = default;
Machine(int st , int wt)
:_starttime(st)
,_worktime(wt)
{}
bool operator()(const Machine& obj1 , const Machine& obj2)
{
return obj1.getsum() > obj2.getsum();
}
};
vector<int> process(vector<int>& arr , int num)
{
vector<int> ans;
priority_queue<Machine , vector<Machine> , Machine> heap;
for (auto x : arr)
{
heap.push(Machine(0 , x));
}
for (int i = 0; i < num; i++)
{
Machine cur = heap.top();
heap.pop();
ans.push_back(cur.getsum());
cur._starttime += cur._worktime;
heap.push(Machine(cur._starttime , cur._worktime));
}
return ans;
}
递归版本
我们在写递归版本的时候首先要想到递归函数的含义
它的含义是返回一个所有咖啡杯都被洗完的最小值
之后我们可以想base case 当什么样的时候 该函数无法递归了
最后列出所有可能性即可
int process(vector<int>& end , int index , int a , int b , int avltime)
{
if (index == static_cast<int>(end.size()))
{
return 0;
}
// possible 1
int p1 = max(a + end[index] , process(end , index+1 , a , b , avltime));
// possible 2
int p2 = max(b + end[index], process(end , index+1 , a , b , avltime + b));
return min(p1 , p2);
}
动态规划
这个问题的动态规划涉及到一个大小问题
因为我们无法确定avltime使用到的时间 所以这里有两种解决方案
- 将它开辟的足够大
- 根据最大值计算 (假设所有人都用咖啡机洗)
int dpprocess(vector<int>& end , int a , int b , vector<vector<int>> dp)
{
// dp[N][...] = 0;
for (int indexdp = static_cast<int>(end.size()) - 1; indexdp >= 0 ; indexdp--)
{
for (int freetime = 0; freetime <= 10000 ; freetime++)
{
int p1 = max(a + end[indexdp] , dp[indexdp+1][freetime]);
int p2 = max(b + end[indexdp] , dp[indexdp+1][freetime+b]);
dp[indexdp][freetime] = min(p1 , p2);
}
}
return dp[0][0];
}