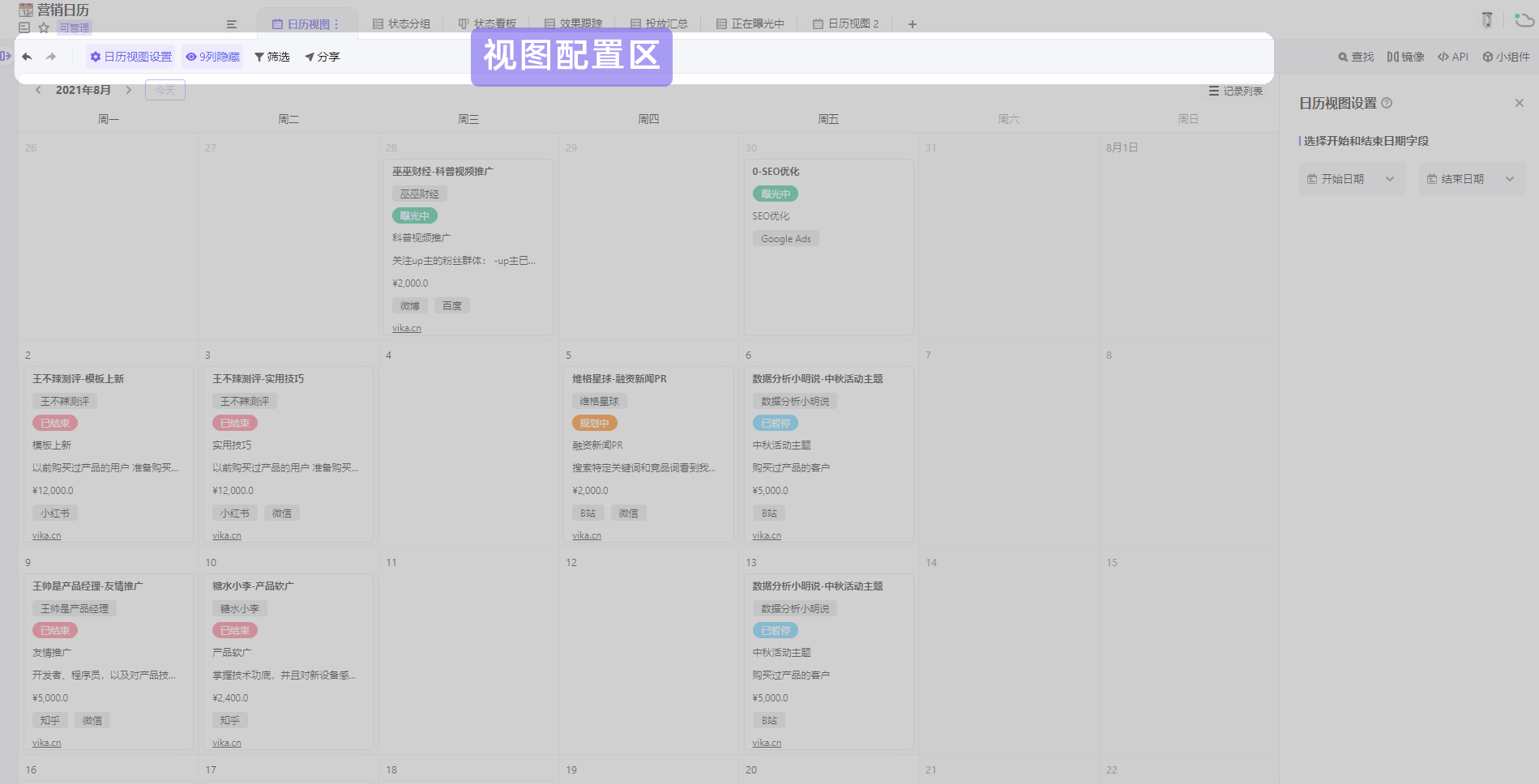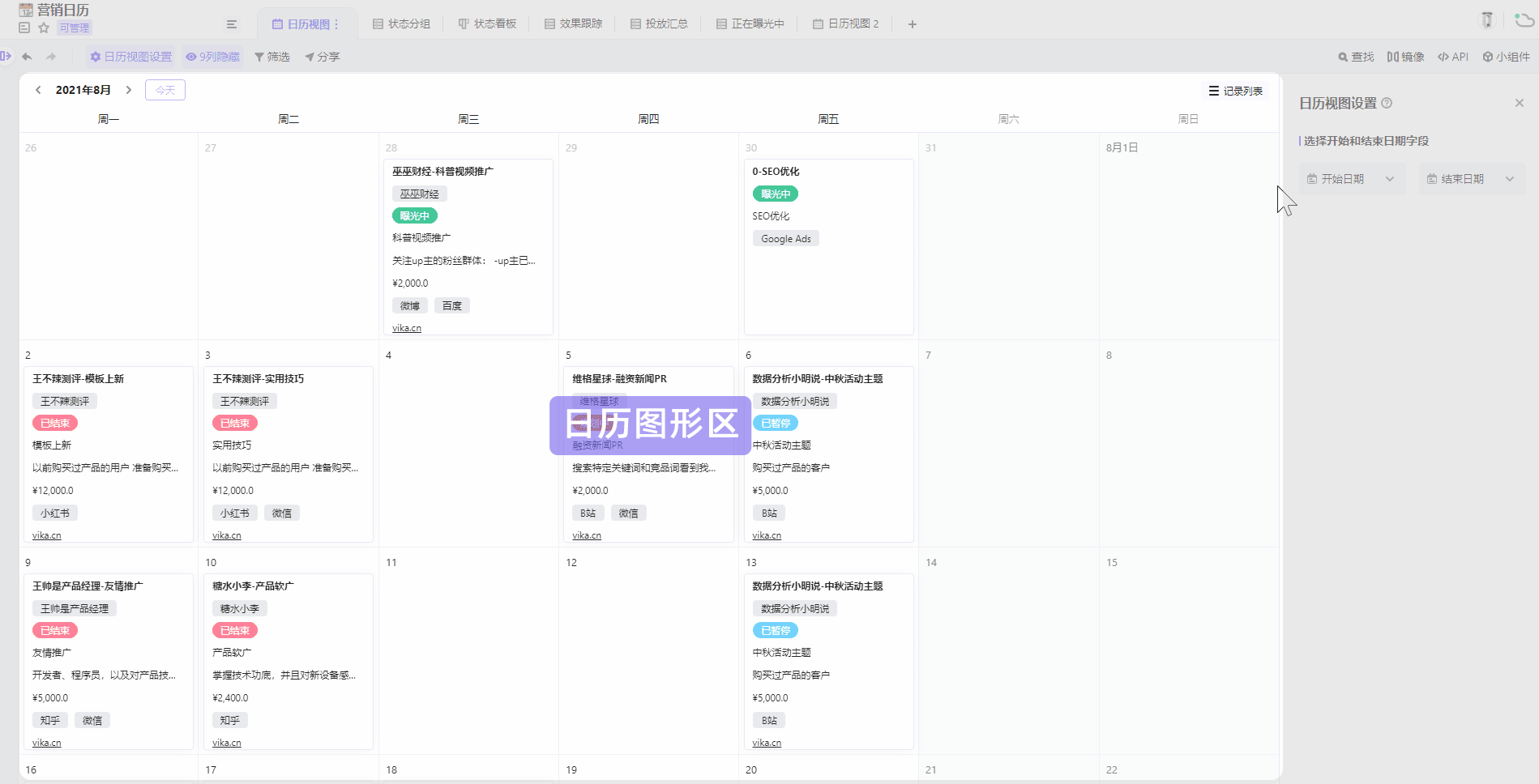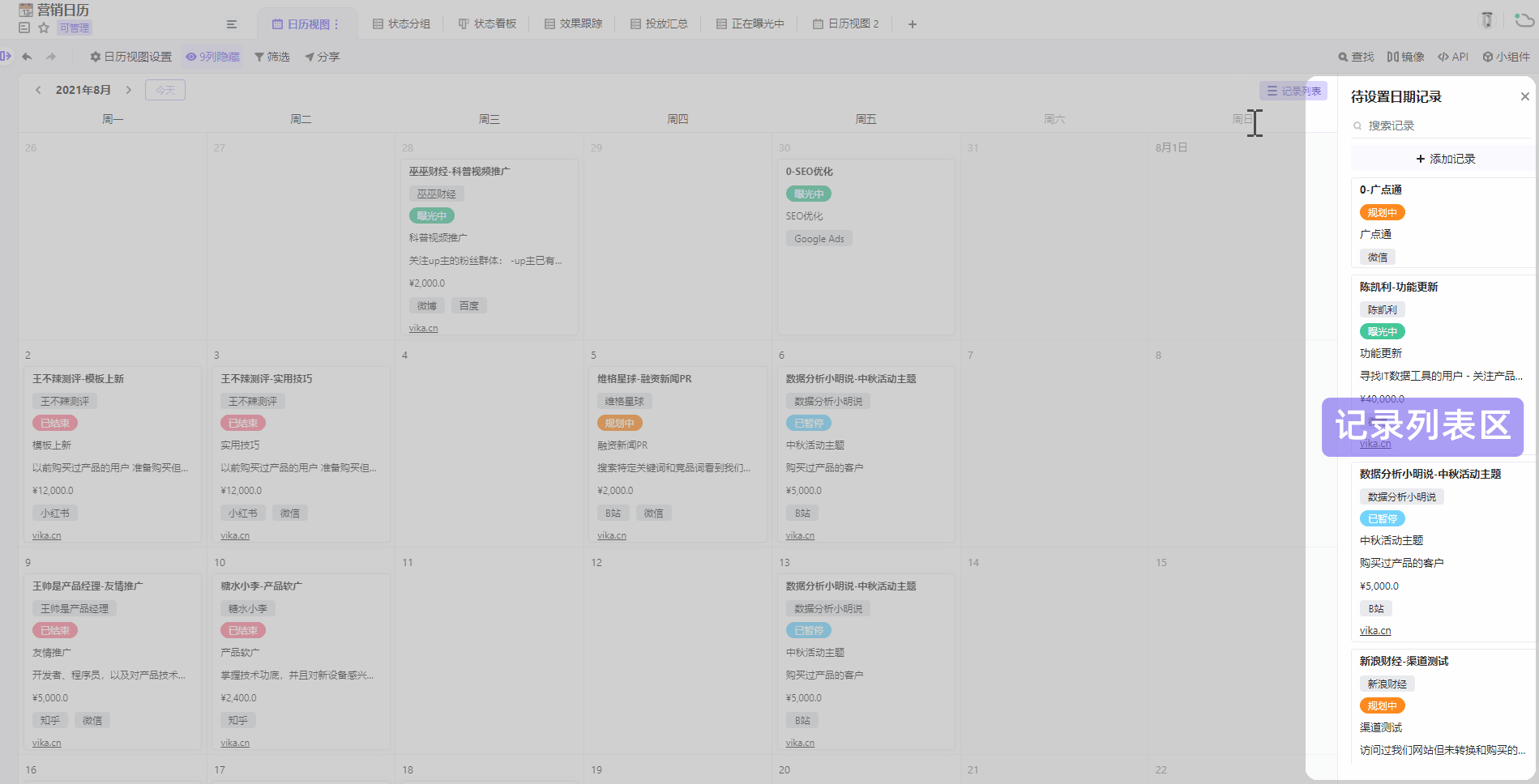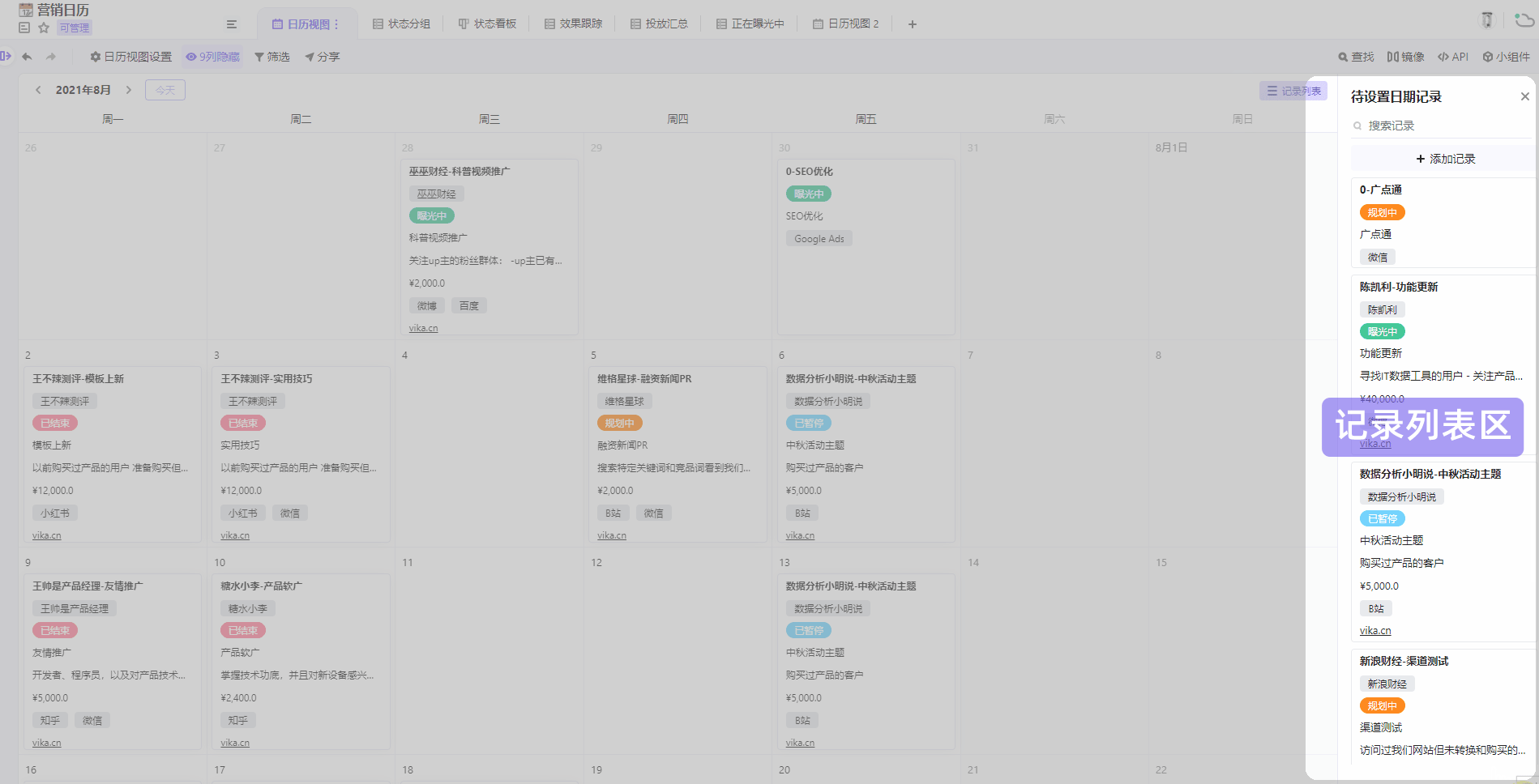
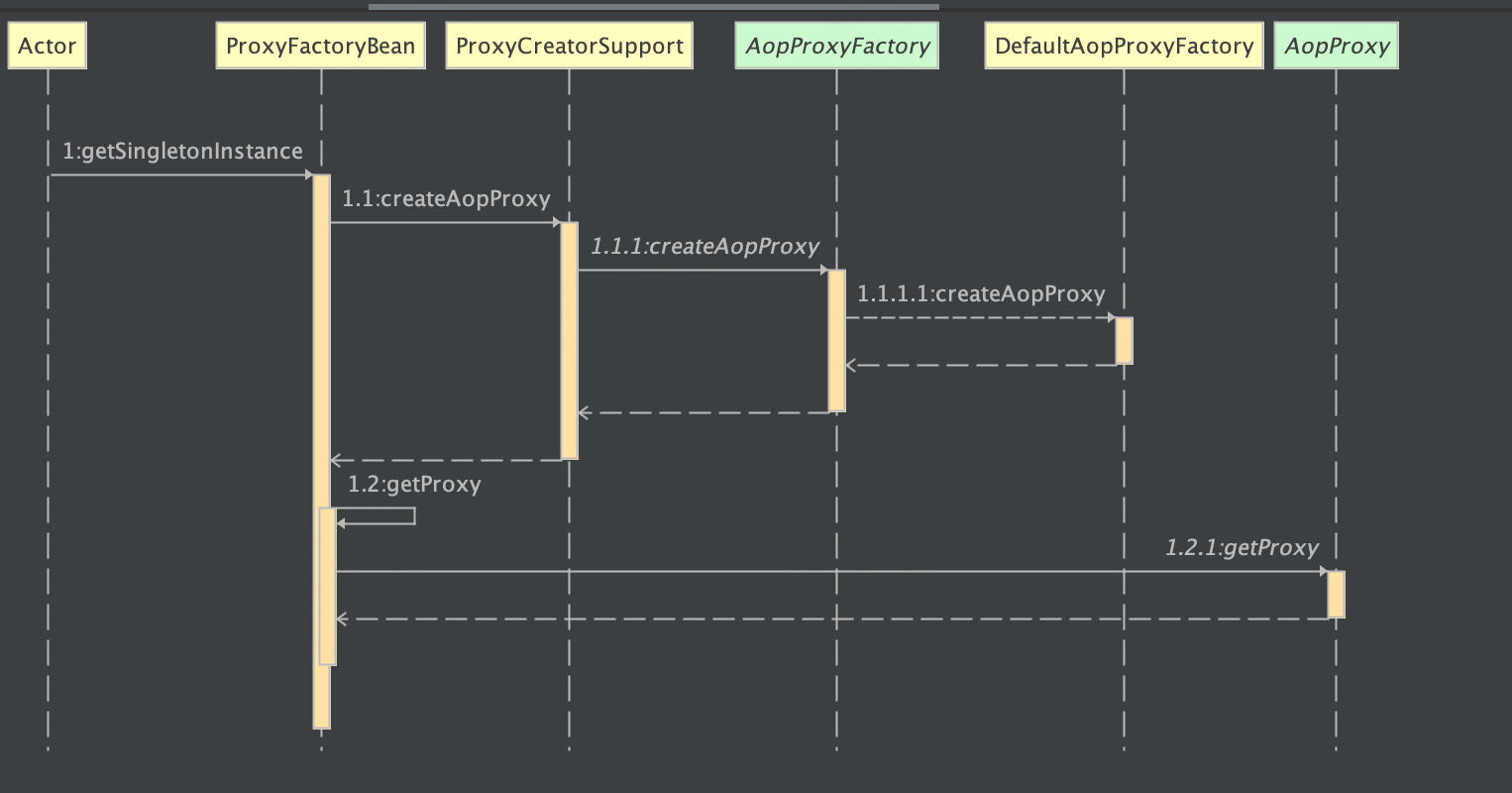
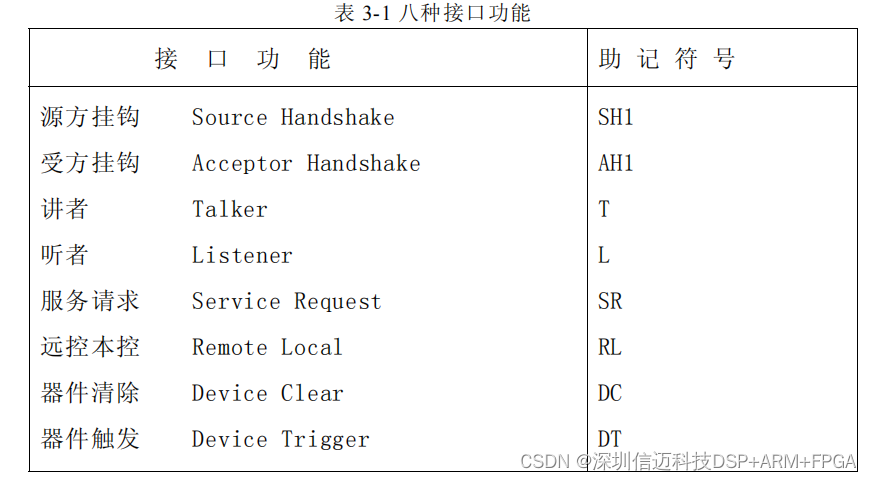
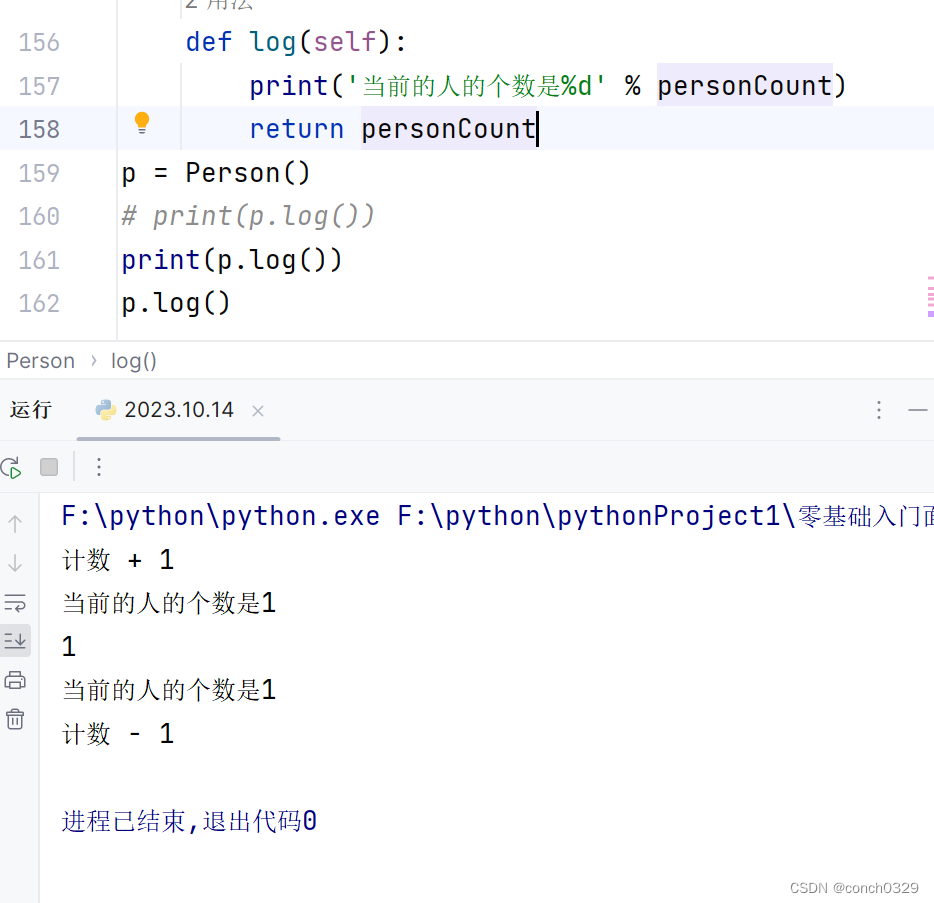
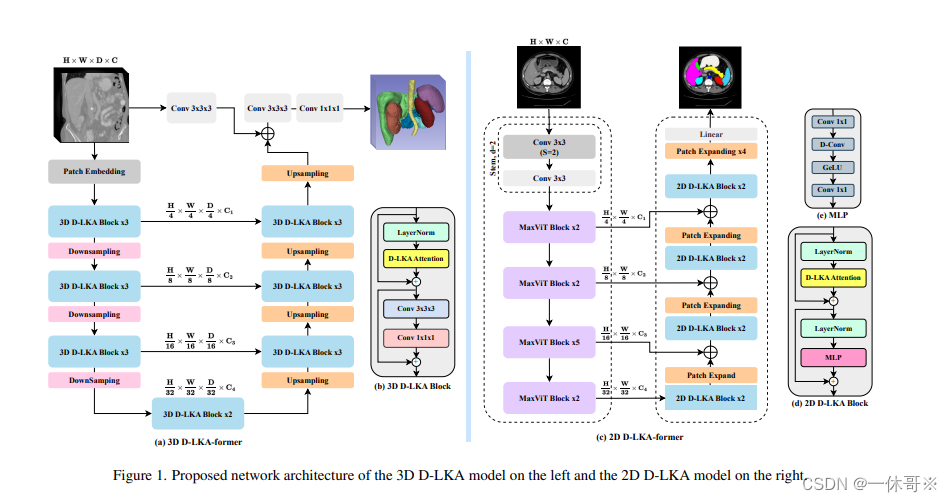
题目大意

题意来源

解题思路

• 首先我们假设存在$x$满足$a,b\in [l,r],gcd(a,b)=x$
• 那么肯定$gcd(\lfloor a/x\rfloor ,\lfloor b/x\rfloor )=1就是互质$
• 假设$a<b$
• 那么$b最小可以取=(\lfloor a/x\rfloor +1)\ast x$ 因为$(\lfloor a/x\rfloor +1)和\lfloor a/x\rfloor$肯定互质
• 那么我们可以贪心的找两个最小的倍数，就是$kx和(k+1)x\in [l,r]$
• 那么分类讨论一下
• • 如果$x\in [l,r]$那么只要$x,2x\in [l,r]$即可
• • 如果$x<l$那么就是公式$kx\ge l\&\&(k+1)x\le r$
• • 那么根据贪心对于同一个$x$,最小的$k=\lceil l/x\rceil$,那么$x\le r/(\lceil l/x\rceil +1)$
• • 看到上面的向上取整，我们可以想到算法数论分块，因为对于同一个范围内的$x$,这个最小的k值都是固定的
• • 现在把$\lceil l/x\rceil =\lfloor (l-1)/x+1\rfloor$就可以带入数论分块了
• • $x\le r/(\lfloor (l-1)/x+1\rfloor +1)$

代码实现

#include <iostream>
#include <cstring>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = 3005;
typedef long long ll;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
const ll mod = 998244353;
vector<int> arr;
ll sum, pre;
int main() {
    // freopen("1.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while(T --) {
        ll l,r;
        scanf("%lld%lld",&l,&r);
		ll ans = max(0ll,r/2-l+1);
		for(ll L = 1, R = 1; L < l; L = R + 1)	{
			ll num = (l-1)/L;
			R = min((l-1)/num,l-1); // 数论分块的右边界
			ll now = r/(num+2); // 上面不等式的右边
			// printf("now = %lld ans = %lld L = %lld R = %lld\n",now,ans,L,R);
			if(now >= L) ans += (min(now,R)-L+1);

		}
		printf("%lld\n",ans);
    } 
    return 0;
}