系列文章目录

第一章 Python 机器学习入门之线性回归
第一章 Python 机器学习入门之梯度下降法
第一章 Python 机器学习入门之牛顿法
第二章 Python 机器学习入门之逻辑回归
番外 Python 机器学习入门之K近邻算法

前言

之前看逻辑回归看的脑壳大，于是跑来看看机器学习中号称最简单的算法之一K近邻算法

一、K近邻算法简介

1、定义

百科定义：
所谓K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也就是上面所说的K个邻居）， 这K个实例的多数属于某个类，就把该输入实例分类到这个类中；

简单来说，就像我们常说的“近朱者赤，近墨者黑”，如果我们不知道一个人的品性，那不妨看看他身边的人的品性，大抵也就能看出来了，这也是K近邻的核心思想，如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别，则该样本也属于这个类别；

2、用途

k近邻可用于回归和分类，在回归问题中通常是得出最近的k个实例的标记值，然后取这k个实例标记值的平均数或中位数，分类问题就不多说了。

二、K近邻应用

这么说可能只有一个概念，我们接下来举个例子来看看它的详细过程

1、问题

作为一名研究生，你如何判断他是否能拿到奖学金呢，我们舍弃掉大部分极端情况，只考虑他在外学习时间和宿舍游戏时间，一般来说在外学习时间越长，拿到奖学金的概率就越大，宿舍游戏时间越长，拿到奖学金概率就越低;

我们使用游戏时间作为x轴，学习时间作为y轴，红色的代表拿到奖学金，绿色的代表没拿到奖学金，学习时间远超过游戏时间的可以视作拿到奖学金，而对于学习时间与游戏时间相近的情况，我们不好判断了，此时就可以使用K近邻算法了；

2、过程

1.假设将图中每位研究生视作一个点，就如上图标记的一样；
2.计算未知点到图中每一个点的欧几里得距离；
3.假设k=4，选取距离未知点最近的4位同学；
4.比较这四位同学中拿到还是未拿到奖学金的数量，如果拿到的同学多，未知点马同学拿到奖学金，如果未拿到的同学多，未知点马同学未拿到奖学金；如果相等，重新选择k值直至确定未知点的状态。

三、k近邻算法详解

1、三要素

k近邻算法的三个基本要素分别是K值的选择、距离度量的方式和分类决策的规则

1.1 k值选择

k值的选择可以说是k近邻最重要的要素了，因为它没有一个固定的选择，在不同的问题我们要找到拟合度最合适的情况，也就是我们经常说的调参（调参侠狂喜.jpg）;
但是K值即参数的选择异常重要，如果如果k值取的越大，则离未来新样本的实例会越来越多，即较远的实例也会对结果造成影响，从而使得模型欠拟合，但是模型会变得简单；反之只有较少的实例会对结果造成影响，模型会变得复杂，同时会使得模型容易发生过拟合现象；通常K值一般小于20

2.2 距离度量的方式

通常有多种方式可选择，包括欧几里得距离，曼哈顿距离和闵可夫斯基距离，常用的还是欧几里得距离； 假设n维空间中有两个点xi和xj，下面是具体的公式；

欧几里得距离

曼哈顿距离

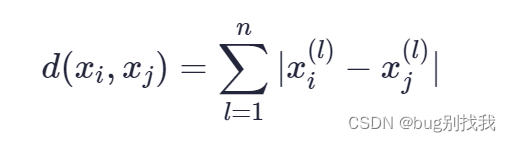
闵可夫斯基距离

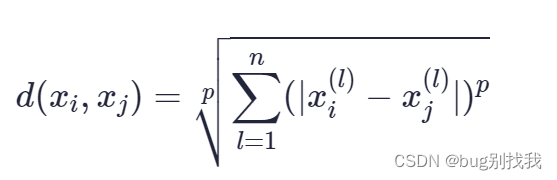
2、维数诅咒

KNN在高维空间运行会出现”维度诅咒”的问题，因为在高维空间太广阔，通过距离度量的方式可以发现即使是最近的邻居在高维空间的距离也很远，以至于很难估计样本之间的距离；
一般情况下可以使用特征选择和降维等方法避免维数诅咒。

四、优缺点

优点：
1.思想简单
2.可用于非线性分类
3.基于实例学习，对数据没有假设，不需要通过模型训练获得参数

缺点：
1.计算量大，空间复杂度高
2.容易被样本影响，一旦样本某特征值影响力过高会导致其他影响力小的特征值失效